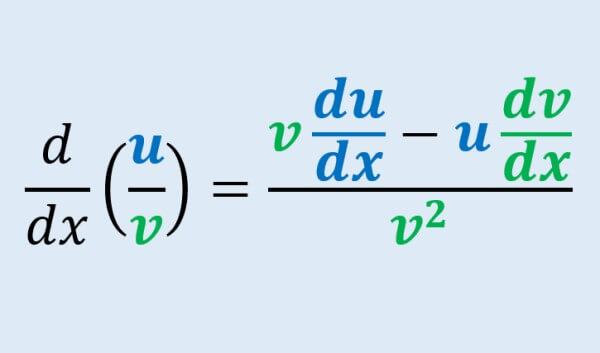A Regra do Quociente é uma das ferramentas mais úteis em Cálculo Diferencial (ou Cálculo I) para derivar um quociente de duas funções. Ela pode ser usada em conjunto com qualquer tipo de função existente, desde que as operações de divisão estejam presentes no problema de diferenciação fornecido.
Aqui, focaremos principalmente em provas da fórmula da regra do quociente usando os conceitos de diferenciação por limites e a regra da cadeia. Além disso, veremos alguns exemplos de funções de diferenciação que usam a fórmula da regra do quociente.
Prova da regra do quociente usando limites
É recomendável que você esteja familiarizado com os tópicos O declive de uma reta tangente e Derivadas usando limites como pré-requisitos para entender melhor a prova da regra do quociente usando limites.
Podemos lembrar que
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Agora vamos usar a seguinte expressão:
$$\Upsilon(x) = \frac{f(x)}{g(x)}$$
Então temos,
$$\Upsilon'(x) = \frac{d}{dx} \left(\frac{f(x)}{g(x)}\right)$$
Usando limites, podemos derivar $latex \Upsilon(x)$ por
$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{\Upsilon(x+h)-\Upsilon(x)}{h}}$$
Substituindo a equação $latex \Upsilon(x) = \frac{f(x)}{g(x)}$, temos
$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{{\frac{f(x+h)}{g(x+h)}} – {\frac{f(x)}{g(x)}}}{h}}$$
Obtendo o menor denominador comum do numerador, temos
$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{\frac{f(x+h) \cdot g(x) – f(x) \cdot g(x+h)}{g(x+h) \cdot g(x)}}{h}}$$
Aplicando as regras das frações, nossa equação pode ser reescrita como:
$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x) – f(x) \cdot g(x+h)}{g(x+h) \cdot g(x) \cdot h}}$$
Agora, podemos adicionar e subtrair o produto de f(x) e g(x), que é $latex f(x)g(x)$, ao numerador $$f(x+h) \cdot g(x) ) – f(x) \cdot g(x+h)g(x+h)$$
Portanto, temos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x) + f(x) \cdot g(x) – f(x) \cdot g(x) – f(x) \cdot g(x+h)}{g(x+h) \cdot g(x) \cdot h}}$$
Como $latex + f(x) \cdot g(x) – f(x) \cdot g(x) = 0$, não alteramos a equação.
Reorganizando a equação acima, temos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x) – f(x) \cdot g(x) – f(x) \cdot g(x+h) + f(x) \cdot g(x)}{g(x+h) \cdot g(x) \cdot h}}$$
Agora, podemos simplificar ainda mais a equação acima fatorando o numerador:
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\frac{g(x) \cdot (f(x+h) – f(x)) – f(x) \cdot (g(x+h) – g(x))}{g(x+h) \cdot g(x) \cdot h}}$$
Então podemos reorganizar a equação assim:
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\left(\frac{1}{g(x+h) \cdot g(x)}\right) \hspace{1.15 pt} \cdot \hspace{1.15 pt} \bigg[\left(g(x) \cdot \left(\frac{f(x+h) – f(x)}{h}\right)\right) – \hspace{1.15 pt} \left(f(x) \cdot \left(\frac{g(x+h) – g(x)}{h}\right)\right)\bigg]}$$
para podermos manipulá-la algebricamente da maneira necessária para provar a regra do quociente.
Aplicando as propriedades dos limites para resolver a equação, temos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\frac{1}{g(x+h) \cdot g(x)}} \hspace{1.15 pt} \cdot \hspace{1.15 pt} \bigg[ \lim \limits_{h \to 0} {g(x)} \hspace{1.15 pt} \cdot \hspace{1.15 pt} \lim \limits_{h \to 0} {\frac{f(x+h) – f(x)}{h}} – \hspace{1.15 pt} \lim \limits_{h \to 0} {f(x)} \hspace{1.15 pt} \cdot \hspace{1.15 pt} \lim \limits_{h \to 0} {\frac{g(x+h) – g(x)}{h}} \bigg]$$
Assim, podemos resolver os limites reconhecendo que a primeira parte de cada termo é simplesmente igual às funções $latex g(x)$ e $latex f(x)$ respectivamente e a segunda parte de cada termo é a derivada em termos de limites de $latex f(x)$ e $latex g(x)$ respectivamente. Portanto, temos:
$$ \frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \left(\frac{1}{g(x) \cdot g(x)}\right) \hspace{1.15 pt} \cdot \hspace{1.15 pt} \Big[ \left( g(x) \cdot \frac{d}{dx}(f(x)) \right) – \hspace{1.15 pt} \left(f(x)\cdot \frac{d}{dx}(g(x)) \right) \Big]$$
Simplificando algebricamente, temos
$$\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{g(x) \cdot \frac{d}{dx}(f(x)) \hspace{1.15 pt} – \hspace{1.15 pt} f(x) \cdot \frac{d}{dx}(g(x))}{(g(x))^2}$$
ou pode ser simplesmente ilustrado como
$$\left(\frac{f}{g}\right)'(x) = \frac{g(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} f'(x) \hspace{2.3 pt} – \hspace{2.3 pt} f(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} g'(x)}{(g(x))^2}$$
que agora é a fórmula para a regra do quociente.
Prova da regra do quociente usando as regras do produto e da cadeia
Outra maneira mais fácil de provar e formular a regra do quociente é aplicando as fórmulas do produto e da regra da cadeia. Portanto, é recomendável que você se familiarize com os tópicos A Fórmula da Regra da Cadeia e A Regra do Produto como pré-requisitos para entender melhor este teste.
Podemos lembrar que a fórmula da regra do produto é
$latex (fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)$
Além da regra do produto, lembramos também que a fórmula da regra da cadeia é
$$\frac{d}{dx} [(f(x))^n] = n \cdot (f(x))^{n-1} \cdot \frac{d}{dx}(f(x))$$
Agora, se temos duas funções f(x) e g(x) e então nos pedem para obter a derivada de $latex \frac{f}{g}(x)$, temos
$$\left(\frac{f}{g}\right)’ (x) = \frac{d}{dx} \left(\frac{f(x)}{g(x)}\right)$$
Reescrevendo o denominador da fração na forma exponencial, temos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{d}{dx} (f(x) \cdot (g(x))^{-1})$$
Agora, podemos derivar o lado direito da equação aplicando a fórmula da regra do produto:
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = f(x) \cdot \frac{d}{dx} (g(x))^{-1}) + (g(x))^{-1} \cdot \frac{d}{dx}(f(x))$$
Para derivar $latex \frac{d}{dx} (g(x))^{-1}$, precisamos usar a fórmula da regra da cadeia. Portanto, temos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = f(x) \cdot \left[(-1) \cdot (g(x))^{-2} \cdot \frac{d}{dx}(g(x)) \right]+ (g(x))^{-1} \cdot \frac{d}{dx}(f(x))$$
Realizando todas as operações aplicáveis, tomando o mínimo denominador comum, reescrevendo o expoente negativo na forma fracionária e seguindo as regras para frações, temos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = f(x) \cdot \left[(-1) \cdot (g(x))^{-2} \cdot (g'(x)) \right]+ (g(x))^{-1} \cdot (f'(x))$$
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = -f(x) \cdot (g(x))^{-2} \cdot (g'(x)) + (g(x))^{-1} \cdot (f'(x))$$
$$ \frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = -f(x) \cdot \frac{1}{(g(x))^2} \cdot (g'(x)) + \frac{1}{g(x)} \cdot (f'(x))$$
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{-f(x) \cdot (g'(x))}{(g(x))^2} + \frac{(f'(x))}{g(x)}$$
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = -\frac{f(x) \cdot (g'(x))}{(g(x))^2} + \frac{g(x) \cdot (f'(x))}{(g(x))^2}$$
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{g(x) \cdot (f'(x))}{(g(x))^2} \hspace{1.15 pt} – \hspace{1.15 pt} \frac{f(x) \cdot (g'(x))}{(g(x))^2}$$
Então finalmente obtemos
$$\left(\frac{f}{g}\right)'(x) = \frac{g(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} f'(x) \hspace{2.3 pt} – \hspace{2.3 pt} f(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} g'(x)}{(g(x))^2}$$
que é a fórmula da regra do quociente.
Prova da regra do quociente usando diferenciação implícita
Na verdade, este é o método mais curto para provar a fórmula da regra do quociente, considerando que você está familiarizado com os tópicos, a regra do produto e a diferenciação implícita.
Podemos lembrar que a diferenciação implícita é usada para funções em uma forma mais complicada onde é difícil ou impossível expressar f(x) ou y explicitamente em termos de x. Por exemplo, temos a equação:
$$y = \frac{u}{v}$$
e então somos solicitados a derivar $latex y$. Diferenciando $latex y$, temos
$$y’ = \left(\frac{u}{v}\right)’$$
Mas assumindo que não podemos simplificar ainda mais nossa equação algebricamente e ainda não conhecemos a fórmula para a regra do quociente, podemos derivá-la aplicando a diferenciação implícita.
Para derivar implicitamente nossa equação dada, devemos primeiro multiplicar algebricamente o denominador do lado direito para o esquerdo da equação. Portanto, temos
$latex vy = u$
Em seguida, derivamos a equação inteira em termos da variável $latex x$:
$$\frac{d}{dx} (vy) = \frac{d}{dx} (u)$$
Para derivar o lado esquerdo da equação, usaremos a regra do produto. Também trataremos $latex v$ e $latex y$ como variáveis e não como constantes. Ao fazer isso, temos
$$vy’ + yv’ = \frac{d}{dx} (u)$$
Como derivamos $latex u$ em termos da variável $latex x$ neste caso? Assim como $latex v$ e $latex y$, trataremos $latex u$ como uma variável, não uma constante. Ao fazer isso, temos
$$vy’ + yv’ = u’$$
Como nos pedem $latex y’$, devemos resolver nossa equação em termos de $latex y’$. Ao fazer isso, temos
$$y’ = \frac{u’-yv’}{v}$$
Mas o que é $latex y$? Podemos lembrar que $latex y = \frac{u}{v}$. Substituindo $latex y$ em nossa equação derivada, temos
$$y’ = \frac{u’-\left(\frac{u}{v}\right) \cdot v’}{v}$$
Simplificando algebricamente, encontrando o menor denominador comum e aplicando as regras das frações, temos
$$y’ = \frac{u’-\left(\frac{u}{v}\right) \cdot v’}{v}$$
$$y’ = \frac{u’-\left(\frac{uv’}{v}\right)}{v}$$
$$y’ = \frac{\left(\frac{vu’}{v}\right)-\left(\frac{uv’}{v}\right)}{v}$$
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’ \hspace{2.3 pt} – \hspace{2.3 pt} uv’}{(v) \cdot (v)}$$
Então finalmente temos
| $latex \frac{d}{dx}(\frac{u}{v}) = \frac{vu’ \hspace{2.3 pt} – \hspace{2.3 pt} uv’}{v^2}$ |
que é a fórmula da regra do quociente.
Veja também
Interessado em aprender mais sobre a regra do quociente? Dê uma olhada nessas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
