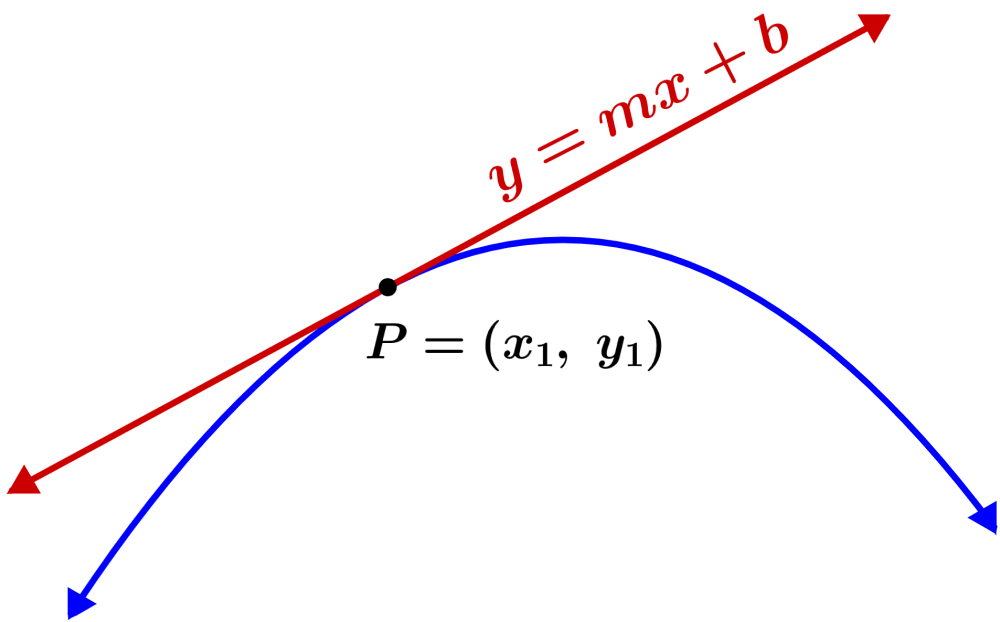
A equação da reta tangente à curva é encontrada usando a forma y=mx+b, onde m é o declive da reta e b é a interseção com y. Por sua vez, encontramos o declive da reta tangente usando a derivada da função e avaliando-a no ponto dado.
A seguir, veremos 10 exercícios nos quais encontraremos a equação da reta tangente a uma curva. Além disso, exploraremos 5 problemas práticos.
Processo para encontrar a equação da reta tangente à curva
A equação da reta tangente à curva pode ser encontrada usando a forma $latex y=mx+b$, onde m é o declive da reta e b é a interseção com y.
Então, se quisermos encontrar a equação da reta tangente à curva no ponto $latex (x_{1},~y_{1})$, podemos seguir estes passos:
1. Encontre a derivada da função que representa a curva.
2. Use a derivada da função para encontrar o declive da reta tangente no ponto $latex (x_{1},~y_{1})$.
Para isso, usamos a coordenada x do ponto na derivada da função. Ou seja, temos $latex m=f'(x_{1})$.
3. Use a equação $latex y=mx+b$ para encontrar o valor de b.
Use o valor do declive encontrado no passo 2 e substitua as coordenadas x e y do ponto dado para encontrar o valor de b. Ou seja, temos $latex y_{1}=mx_{1}=b$.
4. Substitua os valores de m e b na equação $latex y=mx+b$.
Veja os exemplos a seguir para aprender como aplicar esses passos para encontrar a equação da reta tangente à função.
10 Exercícios resolvidos da reta tangente à curva
EXERCÍCIO 1
Qual é a equação da reta tangente à curva $latex f(x)=x^2$ no ponto P=(1, 3)?
Solução
Para encontrar a equação da tangente, podemos usar a forma $latex y=mx+b$, onde m é o declive e b é a interseção com y.
O declive da reta tangente é encontrada calculando a derivada da função no ponto dado. Ou seja, o declive é igual a $latex f'(1)$. Então temos:
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex m=f'(1)=2(1)$
$latex m=2$
Até agora, temos a equação $latex y=2x+b$. Encontramos o valor de b usando o ponto (1, 3) na equação:
$latex y=2x+b$
$latex 3=2(1)+b$
$latex b=1$
A equação da reta tangente no ponto (1, 3) é $latex y=2x+1$.
EXERCÍCIO 2
Encontre a equação da reta tangente à função $latex f(x)=x^3-10x$ no ponto (2, 1).
Solução
Precisamos da derivada da função para encontrar o declive da reta tangente. Então temos:
$latex f(x)=x^3-10x$
$latex f'(x)=3x^2-10$
Para encontrar o declive da reta tangente no ponto (2, 1), avaliamos $latex f'(2)$:
$latex m=f'(2)=3(2)^2-10$
$latex m=2$
Formamos a equação $latex y=2x+b$. Agora, encontramos o valor de b, usando o ponto (2, 1) na equação:
$latex y=2x+b$
$latex 1=2(1)+b$
$latex b=-1$
A equação da reta tangente no ponto (2, 1) é $latex y=2x-1$.
EXERCÍCIO 3
Se tivermos a função $latex f(x)=2x^3-7x^2$, encontre a equação de sua tangente no ponto (2, 3).
Solução
A derivada da função nos permite encontrar o declive da reta tangente. Então a derivada é:
$latex f(x)=2x^3-7x^2$
$latex f'(x)=6x^2-14x$
O declive da reta tangente no ponto (2, 3) é igual a $latex f'(2)$. Então temos:
$latex m=f'(2)=6(2)^2-14(2)$
$latex m=24-28$
$latex m=-4$
Usando o declive encontrado, temos a equação $latex y=-4x+b$. Agora, encontramos o valor de b, usando o ponto (2, 3) na equação:
$latex y=-4x+b$
$latex 3=-4(2)+b$
$latex b=11$
A equação da reta tangente no ponto (2, 3) é $latex y=-4x+11$.
EXERCÍCIO 4
Temos a função $latex f(x)=x^3+\frac{8}{x}$. Qual é a reta tangente no ponto (2, 4)?
Solução
Começamos encontrando a derivada da função:
$latex f(x)=x^3+8x^{-1}$
$latex f'(x)=3x^2-8x^{-2}$
$latex f'(x)=3x^2-\frac{8}{x^2}$
O declive da tangente no ponto (2, 4) é encontrada avaliando $latex f'(2)$. Então temos:
$latex m=f'(2)=3(2)^2-\frac{8}{2^2}$
$latex =12-2$
$latex m=10$
Temos a equação $latex y=10x+b$. Usamos o ponto (2, 4) para encontrar o valor de b:
$latex y=10x+b$
$latex 4=10(2)+b$
$latex b=-15$
A equação da reta tangente no ponto (2, 4) é $latex y=10x-15$.
EXERCÍCIO 5
Qual é a reta tangente a $latex f(x) = -x^{-2}+\sqrt{x}$ no ponto (1, 3)?
Solução
Começamos encontrando a derivada da função para determinar o declive da reta tangente:
$latex f(x)=-x^{-2}+x^{\frac{1}{2}}$
$$f'(x)=2x^{-3}+\frac{1}{2}x^{-\frac{1}{2}}$$
$$f'(x)=\frac{2}{x^3}+\frac{1}{2\sqrt{x}}$$
O declive da tangente no ponto (1, 3) é igual a $latex f'(1)$, então temos:
$$m=f'(1)=\frac{2}{(1)^3}+\frac{1}{2\sqrt{1}}$$
$latex =2+\frac{1}{2}$
$latex m=\frac{5}{2}$
Agora que formamos a equação $latex y=\frac{5}{2}x+b$, usamos o ponto (1, 3) para encontrar o valor de b:
$$y=\frac{5}{2}x+b$$
$$3=\frac{5}{2}(1)+b$$
$latex b=\frac{1}{2}$
A equação da reta tangente no ponto (1, 3) é $latex y=\frac{5}{2}x+\frac{1}{2}$.
EXERCÍCIO 6
Se tivermos a função $latex f(x)=\sin(x)-\cos(x)$, qual é a equação da reta tangente no ponto (0, 1)?
Solução
Começamos encontrando a derivada da função:
$latex f(x)=\sin(x)-\cos(x)$
$latex f'(x)=\cos(x)+\sin(x)$
Agora, sabemos que o declive da reta tangente no ponto (0, 1) é encontrado avaliando $latex f'(0)$. Então temos:
$latex m=f'(0)=\cos(0)+\sin(0)$
$latex m=1+0$
$latex m=1$
Até agora, temos a equação $latex y=x+b$ e podemos usar essa equação com o ponto (0, 1) para encontrar o valor de b, usando o ponto (0, 1) na equação:
$latex y=x+b$
$latex 1=0+b$
$latex b=1$
A equação da reta tangente no ponto (0, 1) é $latex y=x+1$.
EXERCÍCIO 7
Encontre a reta tangente a $latex f(x)=-2\sin(2x)+\cos(3x)$ no ponto (0, 1).
Solução
Precisamos da derivada da função para encontrar o declive da tangente. Então temos:
$latex f(x)=-2\sin(2x)+\cos(3x)$
$latex f'(x)=-4\cos(2x)-3\sin(3x)$
Agora, podemos calcular $latex f'(0)$ para determinar o declive da reta tangente no ponto (0, 1):
$latex m=f'(0)=-4\cos(2(0))-3\sin(3(0))$
$latex m=-4+0$
$latex m=-4$
Usando o declive encontrado, temos a equação $latex y=-4x+b$. Usando esta equação com o ponto (0, 1) encontramos o valor de b:
$latex y=-4x+b$
$latex 1=0+b$
$latex b=1$
A equação da reta tangente no ponto (0, 1) é $latex y=-4x+1$.
EXERCÍCIO 8
Qual é a reta tangente a $latex f(x)=x^2-3x+1$ no ponto onde a curva cruza o eixo y?
Solução
A derivada da função é:
$latex f(x)=x^2-3x+1$
$latex f'(x)=2x-3$
A declaração nos diz que temos que encontrar a reta tangente no ponto onde a curva intercepta o eixo y. Isso acontece quando as coordenadas em x são iguais a 0. Então, temos:
$latex y=x^2-3x+1$
$latex y=0^2-3(0)+1$
$latex y=1$
Portanto, o ponto da tangente é (0, 1). Agora, calculamos $latex f'(0)$ para encontrar o declive da tangente e temos:
$latex m=f'(0)=2(0)-3$
$latex m=-3$
O declive encontrado nos dá a equação $latex y=-3x+b$. Para encontrar o valor de b, usamos o ponto (0, 1) na equação:
$latex y=-3x+b$
$latex 1=-3(0)+b$
$latex b=1$
A equação da reta tangente no ponto (0, 1) é $latex y=-3x+1$.
EXERCÍCIO 9
Encontre as equações das duas retas tangentes a $latex f(x)=x^2-5x+4$ nos pontos onde a função intercepta o eixo x.
Solução
Os pontos onde a função intercepta o eixo x são os zeros da função. Então, começamos encontrando os zeros:
$latex x^2-5x+4=0$
$latex (x-4)(x-1)=0$
A função corta o eixo x quando $latex x=4$ e $latex x=1$. Além disso, os valores de y nesses pontos são 0, então temos (4, 0) e (1, 0).
Agora, encontramos a derivada e avaliamos $latex f'(4)$ e $latex f'(1)$ para determinar os declives das retas tangentes.
$latex f(x)=x^2-5x+4$
$latex f'(x)=2x-5$
$latex f'(4)=2(4)-5=3$
$latex f'(1)=2(1)-5=-3$
Agora, encontramos os valores de b usando a forma $latex y=mx+b$ com os declives encontrados e as coordenadas de cada ponto.
$latex 0=3(4)+b_{1}$
$latex b_{1}=-12$
$latex 0=-3(1)+b_{2}$
$latex b_{2}=3$
Assim, as equações das retas tangentes são $latex y=3x-12$ e $latex y=-3x+3$.
EXERCÍCIO 10
Encontre as duas retas tangentes à função $latex f(x)=x^2$ nos pontos onde $latex y=9$.
Solução
A declaração nos diz que as retas são tangentes nos pontos onde $latex y=9$. Então, temos que encontrar os valores de x quando $latex y=9$:
$latex x^2=9$
$latex x=\pm \sqrt{9}$
$latex x=3~~$ ou $latex ~~x=-3$
Agora, usamos a derivada da função para encontrar os declives das retas avaliando $latex f'(3)$ e $latex f'(-3)$.
$latex f(x)=x^2$
$latex f'(x)=2x$
$latex f'(3)=2(3)=6$
$latex f'(-3)=2(-3)=-6$
Usando a forma $latex y=mx+b$ com os declives encontrados e as coordenadas de cada ponto (os valores de y são 9 em ambos os casos), podemos encontrar os valores de b:
$latex 9=6(3)+b_{1}$
$latex b_{1}=-9$
$latex 9=-6(-3)+b_{2}$
$latex b_{2}=-9$
Assim, as equações das retas tangentes são $latex y=6x-9$ e $latex y=-6x-9$.
Exercícios de reta tangente à curva para resolver
Temos a função $latex f(x)=\frac{9}{x}$. Encontre a reta tangente quando $latex x=-3$.
Escreva a equação na caixa.
Veja também
Interessado em aprender mais sobre equações de retas tangentes e normais a funções? Você pode olhar para estas páginas: