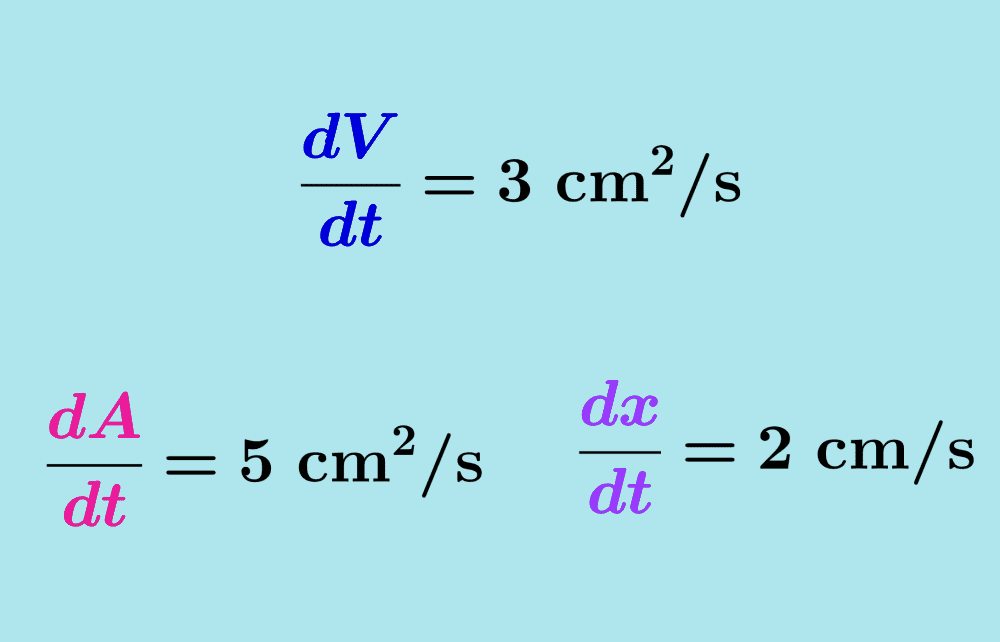Taxa de variação com derivadas – Exercícios resolvidos

Para resolver este problema, temos de começar por encontrar uma equação para a área da peça quadrada de metal.

Se representarmos os lados da peça de metal com $latex x$, sua área é $latex A=x^2$.

Temos que a taxa de variação do comprimento de um lado em relação ao tempo, ou seja, $latex \dfrac{dx}{dt}$, é de 0,1 cm/s.

Queremos encontrar a taxa de variação da área em relação ao tempo, ou seja, $latex \dfrac{dA}{dt}$.

Se derivarmos $latex A=x^2$, temos $latex {dA}{dx}=2x$. Além disso, como $latex \dfrac{dx}{dt}=0,1$, podemos usar a regra da cadeia:

$$\dfrac{dA}{dt}=\dfrac{dA}{dx}\dfrac{dx}{dt}$$

$latex =2x \times 0,1$

$$\dfrac{dA}{dt}=0,2x$$

A taxa de variação da área é de $latex 0,2x$ cm²/s.

Mais uma vez, começamos por encontrar uma equação para a área do quadrado em termos de seus lados.

Se representarmos os lados do quadrado com $latex x$, sua área é $latex A=x^2$.

A partir da pergunta, sabemos a taxa de variação do comprimento de um lado em relação ao tempo, ou seja, $latex \dfrac{dx}{dt}=$ é 5 cm/s.

Para encontrar a taxa de variação da área, ou seja, $latex \dfrac{dA}{dt}$, derivamos $latex A=x^2$ e usamos a regra da cadeia:

$$\dfrac{dA}{dt}=\dfrac{dA}{dx}\dfrac{dx}{dt}$$

$latex =2x \times 5$

$$\dfrac{dA}{dt}=10x$$

Quando o comprimento de um lado é 10 cm, a taxa de variação da área do quadrado é $latex 10(10)=100$ cm²/s.

Neste caso, temos um círculo. A equação da área em relação ao raio do círculo é $latex A=\pi r^2$.

Se derivarmos $latex A=\pi r^2$ em relação ao raio, teremos $latex \dfrac{dA}{dr}=2\pi r$.

Agora, a partir da pergunta, sabemos que a taxa de variação do raio do círculo em relação ao tempo, ou seja, $latex \dfrac{dr}{dt}$, é $latex \frac{1}{3}$ cm /s.

Assim, para encontrar a taxa de variação da área em relação ao tempo, ou seja, $latex \dfrac{dA}{dt}$, podemos usar a regra da cadeia:

$$\dfrac{dA}{dt}=\dfrac{dA}{dr}\dfrac{dr}{dt}$$

$latex =2\pi r \times \frac{1}{3}$

$$\dfrac{dA}{dt}=\frac{2\pi r}{3}$$

Quando o raio é de 5 cm, a taxa de variação da área do círculo é $latex \frac{2\pi (5)}{3}=\frac{10\pi}{3}$ cm²/s .

Como já sabemos, a área de um quadrado em relação aos seus lados pode ser representada pela equação $latex A=x^2$, onde x é um lado.

Agora, resolvendo para $latex x$, temos $latex x=\sqrt{A}$. Ao diferenciar, temos $latex \dfrac{dx}{dA}=\frac{1}{2\sqrt{A}}$.

Nesse caso, temos que a taxa de variação da área do quadrado em relação ao tempo, ou seja, $latex \dfrac{dA}{dt}$, é de 7 cm²/s.

Assim, encontramos a taxa de variação do comprimento de um lado em relação ao tempo, ou seja, $latex \dfrac{dx}{dt}$, usando a regra da cadeia:

$$\dfrac{dx}{dt}=\dfrac{dA}{dt}\dfrac{dx}{dA}$$

$$=7 \times \frac{1}{2\sqrt{A}}$$

$$\dfrac{dx}{dt}=\frac{7}{2\sqrt{A}}$$

Quando a área é de 100 cm², a taxa de variação de um lado do quadrado é $latex \frac{7}{2\sqrt{100}}=\frac{7}{20}$ cm/s.

Podemos representar a área de um círculo em relação ao raio com a equação $latex A=\pi r^2$.

Quando derivamos esta equação em relação a $latex r$, temos $latex \dfrac{dA}{dr}=2 \pi r$.

Temos que a taxa de variação da área do círculo em relação ao tempo, ou seja, $latex \dfrac{dA}{dt}$, é (4π) cm²/s.

Agora, para encontrar a taxa de variação do raio em relação ao tempo, ou seja, $latex \dfrac{dr}{dt}$, usamos a regra da cadeia:

$$\dfrac{dr}{dt}=\dfrac{dA}{dt}\dfrac{dr}{dA}$$

Notamos que $latex \dfrac{dr}{dA}$ é o recíproco de $latex \dfrac{dA}{dr}$. Então temos:

$$\dfrac{dr}{dt}=4\pi \times \dfrac{1}{2 \pi r}$$

$$\dfrac{dr}{dt}=\frac{2}{r}$$

Quando o raio é $latex \frac{1}{2}$ cm, a taxa de variação do raio do círculo é $latex \frac{2}{\frac{1}{2}}=4$ cm/ s.

Se usarmos $latex x$ para representar os lados do cubo, seu volume é $latex V=x^3$.

Resolvendo para $latex x$, temos $latex x=\sqrt[3]{V}$. Derivando, temos $latex \dfrac{dx}{dV}=\frac{1}{3\sqrt[3]{V}}$.

Como a questão nos diz que o volume do cubo está aumentando a uma taxa de 18 cm³/s, temos $latex \dfrac{dV}{dt}=18$ cm³/s.

Assim, encontramos a taxa de variação de um lado do cubo em relação ao tempo, $latex \dfrac{dx}{dt}$, aplicando a regra da cadeia:

$$\dfrac{dx}{dt}=\dfrac{dV}{dt}\dfrac{dx}{dV}$$

$latex =18 \times \frac{1}{3\sqrt[3]{V}}$

$$\dfrac{dA}{dt}=\frac{18}{3\sqrt[3]{V}}$$

Quando o volume é 125 cm³, a taxa de variação de um lado do cubo é $latex \frac{18}{3\sqrt[3]{125}}=\frac{6}{25}$ cm/s.

Se representarmos o raio por $latex r$ e o volume por $latex V$, temos $latex V=\frac{4}{3}\pi r^3$. Então sua derivada é:

$$\dfrac{dV}{dr}=4\pi r^2$$

Da pergunta, temos $latex \dfrac{dV}{dt}=3$. Então, usando a regra da cadeia, temos:

$$\dfrac{dV}{dt}=\dfrac{dV}{dr}\dfrac{dr}{dt}$$

$$3=4\pi r^2 \times \dfrac{dr}{dt}$$

$$\dfrac{dr}{dt}=\frac{3}{4\pi r^2}$$

Quando $latex r=2$, temos:

$$\frac{dr}{dt}\Big|_{r=2}=\frac{3}{4\pi (2)^2}=\frac{3}{16\pi}$$

A taxa de variação do raio quando o raio é de 2 cm é $latex \frac{3}{16\pi}$ cm/s.

Quando representamos o raio por $latex r$ e a área de superfície por $latex As_{s}$, temos $latex As_{s}=4\pi r^2$.

Como conhecemos a área da superfície, precisamos escrever uma equação de $latex r$ em relação a A: $latex r=\sqrt{\frac{A_{s}}{4\pi}}$. Sua derivada é:

$$\dfrac{dr}{dA_{s}}=\frac{1}{4\sqrt{\pi A_{s}}}$$

Temos a informação $latex \dfrac{dA_{s}}{dt}=2$. Assim, aplicando a regra da cadeia, temos:

$$\dfrac{dr}{dt}=\dfrac{dA_{s}}{dt}\dfrac{dr}{dA_{s}}$$

$$=2 \times \frac{1}{4\sqrt{\pi A_{s}} }$$

$$\dfrac{dr}{dt}=\frac{1}{2\sqrt{\pi A_{s}}}$$

Quando $latex A_{s}=100\pi$, temos:

$$\frac{dr}{dt}\Big|_{A_{s}=2}=\frac{1}{2\sqrt{100\pi^2}}=\frac{1}{20\pi}$$

A taxa de variação do raio quando a área da superfície é 100π é $latex \frac{1}{20\pi}$ cm/s.

Representando o raio por $latex r$ e a área de superfície por $latex A_{s}$, temos $latex V=\frac{4}{3}\pi r^3$ e $latex A_{s}=4 \pi r^2$. Então suas derivadas são:

$$\dfrac{dV}{dr}=4\pi r^2$$

$$\dfrac{dA_{s}}{dr}=8\pi r$$

Sabemos que $latex \dfrac{dV}{dt}=10$. Então, usando a regra da cadeia, temos:

$$\dfrac{dA_{s}}{dt}=\dfrac{dV}{dt}\dfrac{dA_{s}}{dr}\dfrac{dr}{dV}$$

$$=10 \times 8\pi r \times \frac{1}{4\pi r^2}$$

$$\dfrac{dA_{s}}{dt}=\frac{20}{r}$$

Quando $latex r=5$, temos:

$$\frac{dA_{s}}{dt}\Big|_{r=5}=\frac{20}{5}=4$$

A taxa de variação da área da superfície quando o raio é de 5 cm é de 4 cm²/s.

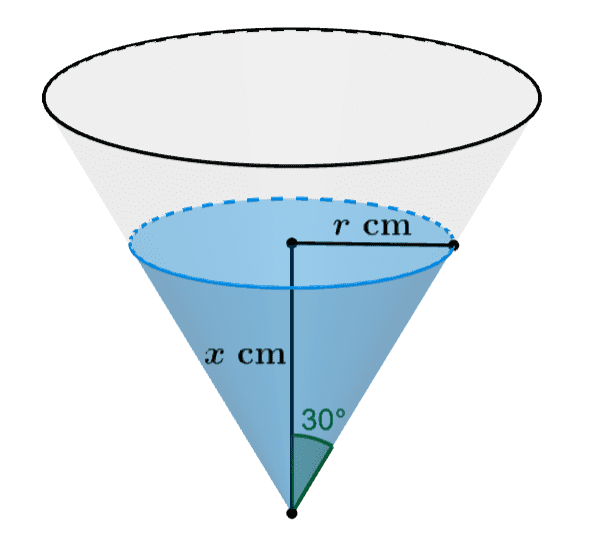
Podemos usar o seguinte diagrama para facilitar a resolução:

A profundidade da água no cone é representada por $latex x$. Então, o raio $látex r$ da seção transversal da água é dado por:

$$\tan(30^{\circ})=\frac{r}{x}$$

$$r=x\tan(30^{\circ})$$

$$=\frac{x}{\sqrt{3}}$$

O volume de água no cone é dado por:

$$V=\frac{1}{3}\pi r^2x$$

$$=\frac{1}{3}\pi \left(\frac{x}{\sqrt{3}}\right)^2x$$

$$=\frac{1}{9}\pi x^3$$

Assim, a derivada do volume em relação a $latex x$ é:

$$\dfrac{dV}{dx}\pi x^2$$

Pela pergunta, sabemos que $latex \dfrac{dV}{dt}=5$. Além disso, pela regra da cadeia, temos:

$$\dfrac{dV}{dt}=\dfrac{dV}{dx} \dfrac{dx}{dt}$$

Então,

$$ 5= \frac{1}{3}\pi x^2 \dfrac{dx}{dt}$$

$$ \dfrac{dx}{dt}= \frac{15}{\pi x^2}$$

Quando $latex x=10$, temos:

$$\dfrac{dx}{dt}=\frac{15}{\pi (10)^2}=\frac{3}{20\pi}$$

A taxa de variação de profundidade quando a profundidade é de 10 cm é $latex \frac{3}{20\pi}$ cm/s.