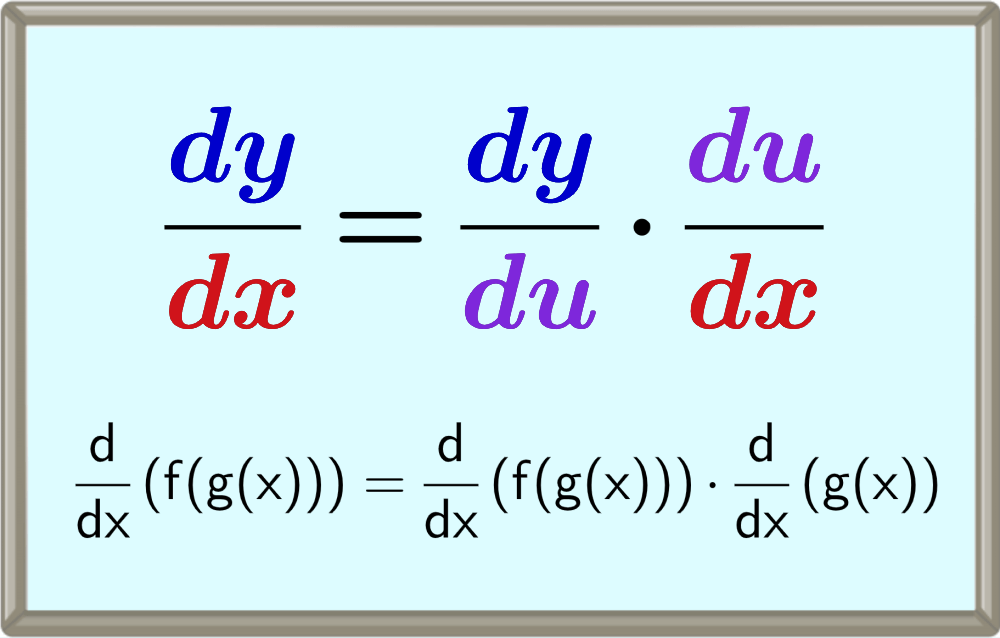A Regra da Cadeia é uma das técnicas das derivadas mais comuns aplicadas no Cálculo Diferencial (ou Cálculo I). Esta regra é usada para derivar uma composição de funções. A regra da cadeia pode ser provada usando um dos pilares do cálculo, os limites.
Neste artigo, exploraremos tudo sobre a regra da cadeia. Abordaremos sua definição, fórmula e aplicações. Também veremos alguns exemplos e problemas práticos para aplicar os princípios da regra da cadeia.
- A regra da cadeia e a sua fórmula
- Como utilizar a regra de cadeia, um tutorial passo-a-passo
- Regra da cadeia – Exemplos com respostas
- Regra da cadeia derivada – Problemas práticos
- Veja também
- A regra da cadeia e sua fórmula
- A diferença entre a regra da cadeia e a regra da potência
- Provas da regra da cadeia
- Quando usar a regra da cadeia para encontrar derivadas
- Como usar a regra da cadeia, um tutorial passo a passo
- Regra da cadeia – Exemplos com respostas
- Regra da cadeia – Problemas de prática
- Veja também
A regra da cadeia e a sua fórmula
O que é a regra da cadeia de derivadas?
A regra da cadeia é definida como a derivada de uma composição de pelo menos dois tipos diferentes de funções como, por exemplo:
$$y’ = \frac{d}{dx}[f \left( g(x) \right)]$$
onde g(x) é o domínio da função f(u).
Também podemos chamar a função f como a função externa e a função g como a função interna. Nesta composição, f(x) e g(x) devem ser dois tipos diferentes de funções que não podem ser avaliadas algebricamente num único tipo de função.
Lembre-se de que uma composição de funções pode ser considerada uma função dentro de uma função ou como uma função de outra função.
A fórmula da regra da cadeia das derivadas
A fórmula da regra da cadeia pode ser expressa verbalmente como a derivada da função externa f multiplicada pela derivada da função interna g. A função interna g é o domínio da derivada da função externa f.
A fórmula da regra da cadeia pode ser ilustrada da seguinte forma:
$$\frac{d}{dx} (f(g(x))) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{dx}(g(x))$$
onde derivamos f(g(x)) usando o método da função f e usando g(x) como domínio da função f e depois multiplicando a derivada da função f pela derivada de g(x).
De outra forma, também pode ser ilustrado como:
$$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$$
onde
- $latex f(u) =$ a função externa
- $latex u = g(x)$, o domínio da função externa $latex f(u)$
- $latex \frac{dy}{du} =$ a derivada da função externa $latex f(u)$ em termos de $latex u$
- $latex \frac{du}{dx} =$ la derivada da função interna $latex g(x)$ em termos de $latex x$
Para mais informações sobre como provar a regra da cadeia usando limites, visite o nosso artigo sobre como provar a regra da cadeia.
Como utilizar a regra de cadeia, um tutorial passo-a-passo
Suponhamos que temos de derivar
$latex H(x) = \sin{(x^3)}$
Como se pode ver, esta dada função pode ser considerada uma função composta. Portanto, podemos utilizar a fórmula da regra da cadeia para derivar este problema.
1. Escrevemos a fórmula para a regra da cadeia como uma referência:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Pode utilizar qualquer forma da fórmula da regra da cadeia.
2. Identificar as funções externas e internas.
Se considerarmos a função interna como $latex g(x) = u=x^3$, então
$latex f(g(x)) = f(u)$
$latex f(u) = \sin{(u)}$
3. Aplicar a fórmula da regra da cadeia.
$$\frac{d}{dx} H(x) = \frac{d}{du}(f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(\sin{(u)}) \cdot \frac{d}{dx}(x^3)$$
$$\frac{d}{dx} H(x) = (\cos{(u)}) \cdot (3x^2)$$
4. Substituir a função interna $latex g(x)=u=x^3$ na equação derivada:
$$\frac{d}{dx} H(x) = (\cos{(x^3)}) \cdot (3x^2)$$
5. Simplificar a derivada obtida:
$$\frac{d}{dx} H(x) = 3x^2 \cdot \cos{(x^3)}$$
$latex H'(x) = 3x^2 \cos{(x^3)}$
Regra da cadeia – Exemplos com respostas
EXEMPLO 1
Derivar a seguinte função:
$latex H(x) = (12x+6)^{24}$
Solução
Passo 1: Escrever a fórmula para a regra da cadeia como referência:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Passo 2: Reconhecendo as duas funções, temos
Se $latex g(x) = u=12x+6$, então
$latex f(g(x)) = f(u)$
$latex f(u) = u^{24}$
Passo 3: Vamos agora aplicar a fórmula da regra da cadeia:
$$\frac{d}{dx} H(x) = \frac{d}{du}(f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(u^{24}) \cdot \frac{d}{dx}(12x+6)$$
$$\frac{d}{dx} H(x) = (24u^{23}) \cdot (12)$$
Passo 4: Substituir a função interna $latex g(x)$ na equação derivada:
$$\frac{d}{dx} H(x) = (24(12x+6)^{23}) \cdot (12)$$
Passo 5: Simplificar algebricamente:
$$\frac{d}{dx} H(x) = 288 \cdot (12x+6)^{23}$$
$latex H'(x) = 288(12x+6)^{23}$
EXEMPLO 2
Encontrar a derivada da função dada.
$latex f(x) = \sqrt[12]{6x-3}$
Solução
Passo 1: Lista a fórmula da regra da cadeia como uma referência:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Passo 2: Se $latex g(x) = u=6x-3$, então
$latex f(g(x)) = f(u)$
$latex f(u) = \sqrt[12]{u}$
$latex f(u) = u^{\frac{1}{12}}$
Passo 3: Vamos agora aplicar a fórmula da regra da cadeia:
$$\frac{d}{dx} H(x) = \frac{d}{du}(f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(u^{\frac{1}{12}}) \cdot \frac{d}{dx}(6x-3)$$
$$\frac{d}{dx} H(x) = \left(\frac{1}{12}u^{-\frac{11}{12}} \right) \cdot (6)$$
Passo 4: Substituir a função interna $latex g(x)=u=6x-3$ na equação derivada.:
$$\frac{d}{dx} H(x) = \left(\frac{1}{12} \cdot (6x-3)^{-\frac{11}{12}} \right) \cdot (6)$$
Passo 5: Simplificar algebricamente:
$$\frac{d}{dx} H(x) = \frac{6}{12 \cdot (6x-3)^{\frac{11}{12}}}$$
$$\frac{d}{dx} H(x) = \frac{1}{2 \cdot (6x-3)^{\frac{11}{12}}}$$
$$H'(x) = \frac{1}{2 \sqrt[12]{(6x-3)^{11}}}$$
em forma radical
EXEMPLO 3
Derivar a seguinte função:
$latex \cos{(12x^2+6x-3)}$
Solução
Passo 1: Começamos com a fórmula da regra da cadeia:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Passo 2: Neste exemplo, temos $latex g(x) = u=12x^2+6x-3$, portanto
$latex f(g(x)) = f(u)$
$latex f(u) = \cos{(u)}$
Passo 3: Vamos agora aplicar a fórmula da regra da cadeia:
$$\frac{d}{dx} H(x) = \frac{d}{du}(f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(\cos{(u)}) \cdot \frac{d}{dx}(12x^2+6x-3)$$
$$\frac{d}{dx} H(x) = (-\sin{(u)}) \cdot (24x+6)$$
Passo 4: Substituir a função interna $latex g(x)=u$ na equação derivada:
$$\frac{d}{dx} H(x) = (-\sin{(12x^2+6x-3)}) \cdot (24x+6)$$
Passo 5: Simplificar algebricamente:
$$\frac{d}{dx} H(x) = -(24+6) \cdot \sin{(12x^2+6x-3)}$$
$$H'(x) = – (24 + 6) \sin{(12x^2+6x-3)}$$
EXEMPLO 4
Qual é a derivada da função dada?
$latex \csc{\ln{(12x+6)}}$
Solução
Passo 1:A fórmula para a regra da cadeia é:
$$ \frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Passo 2: Identificar quantas funções tem no problema. Neste exemplo, há três. Ao separarmos estas três funções, temos
Se $latex g(h(x)) = u$, então
$latex f(g(h(x))) = f(u)$
$latex f(u) = \csc{(u)}$
Se $latex g(h(x)) = v$, então
$latex g(h(x)) = g(v)$
$latex g(v) = \ln{(v)}$
$latex v = h(x) = 12x+6$
Se $latex f(g(h(x))) = f(u)$, então
$$\frac{d}{dx} [f(g(h(x)))] = \frac{d}{du} [f(u)]$$
Se $latex g(h(x)) = g(v)$, então
$$\frac{d}{dx} [g(h(x))] = \frac{d}{dv} [g(v)]$$
Passo 3: Vamos agora aplicar a fórmula da regra da cadeia:
$$f_{1…n}'(x) = f_1′ \left( f_{2…n}(x) \right) \cdot f_2′ \left( f_{3…n}(x) \right)\cdots f_{n-1}’ \left(f_{n…n}(x)\right) \cdot f_n'(x)$$
$$\frac{d}{dx} H(x) = \frac{d}{du} f(u) \cdot \frac{d}{dv} g(v) \cdot \frac{d}{dx} h(x)$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(\csc{(u)}) \cdot \frac{d}{dv}(\ln{(v)}) \cdot \frac{d}{dx}(12x+6)$$
$$\frac{d}{dx} H(x) = (-\csc{(u)} \cot{(u)}) \cdot (\frac{1}{v}) \cdot {12}$$
Passo 4: Substituir $latex g(h(x))$ e $latex h(x)$ em $latex u$ e $latex v$:
$$\frac{d}{dx} H(x) = (-\csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})})\cdot (\frac{1}{12x+6}) \cdot {12}$$
Passo 5: Simplificar:
$$\frac{d}{dx} H(x) = \frac{-12 \csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})}}{12x+6}$$
$$\frac{d}{dx} H(x) = \frac{-12 \csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})}}{6(x+2)}$$
$$\frac{d}{dx} H(x) = \frac{-2 \csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})}}{(x+2)}$$
$$H'(x) = -\frac{2 \csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})}}{(x+2)}$$
EXEMPLO 5
Deriva o seguinte:
$latex e^{\sin^{2}{(6x-3)}}$
Solução
Passo 1: Escreva a fórmula da regra da cadeia como referência:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Passo 2: Identificar quantas funções tem no problema. Neste exemplo, há quatro. Ao listar estas quatro funções, temos
Se $latex f(g(h(j(x)))) = u$, então
$latex f(g(h(j(x)))) = f(u)$
$latex f(u) = e^u$
Se $latex g(h(j(x))) = v$, então
$latex g(h(j(x))) = g(v)$
$latex g(v) = v^2$
Se $latex h(j(x)) = w$, então
$latex h(j(x)) = h(w)$
$latex h(w) = \sin{(w)}$
$latex w = j(x) = 6x-3$
Se $latex f(g(h(j(x)))) = f(u)$, então
$$\frac{d}{dx} [f(g(h(j(x))))] = \frac{d}{du} [f(u)]$$
Se $latex g(h(j(x))) = g(v)$, então
$$\frac{d}{dx} [g(h(j(x)))] = \frac{d}{dv} [g(v)]$$
Se $latex h(j(x)) = h(w)$, então
$$\frac{d}{dx} [h(j(x))] = \frac{d}{dw} [h(w)]$$
Passo 3: Vamos agora aplicar a fórmula da regra da cadeia:
$$f_{1…n}'(x) = f_1′ \left( f_{2…n}(x) \right) \cdot f_2′ \left( f_{3…n}(x) \right)\cdots f_{n-1}’ \left(f_{n…n}(x)\right) \cdot f_n'(x)$$
$$\frac{d}{dx} H(x) = \frac{d}{du} f(u) \cdot \frac{d}{dv} g(v) \cdot \frac{d}{dw} h(w) \cdot \frac{d}{dx} j(x)$$
$$\frac{d}{dx} H(x) = \frac{d}{du} (e^u) \cdot \frac{d}{dv} (v^2)\cdot \frac{d}{dw} (\sin{(w)}) \cdot \frac{d}{dx} (6x-3)$$
$$\frac{d}{dx} H(x) = (e^u) \cdot (2v) \cdot (\cos{(w)}) \cdot (6)$$
Passo 4: Substituir $latex g(h(j(x)))$, $latex h(j(x))$, e $latex j(x)$ em $latex u$, $latex v$, e $latex w$:
$$\frac{d}{dx} H(x) = (e^{\sin^{2}{(6x-3)}}) \cdot (2(\sin{(6x-3)}))\cdot (\cos{(6x-3)}) \cdot (6)$$
Passo 5: Simplificar:
$$\frac{d}{dx} H(x) = 12 \cdot \sin{(6x-3)} \cdot \cos{(6x-3)} \cdot e^{\sin^{2}{(6x-3)}}$$
$$H'(x) = 12 \sin{(6x-3)} \cos{(6x-3)} e^{\sin^{2}{(6x-3)}}$$
Regra da cadeia derivada – Problemas práticos
Obtenha a derivada de $latex f(x) = \ln{(e^x)}$
Escreva a resposta na caixa.
Veja também
Interessado em aprender mais sobre a regra da cadeia? Dê uma olhada nessas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
