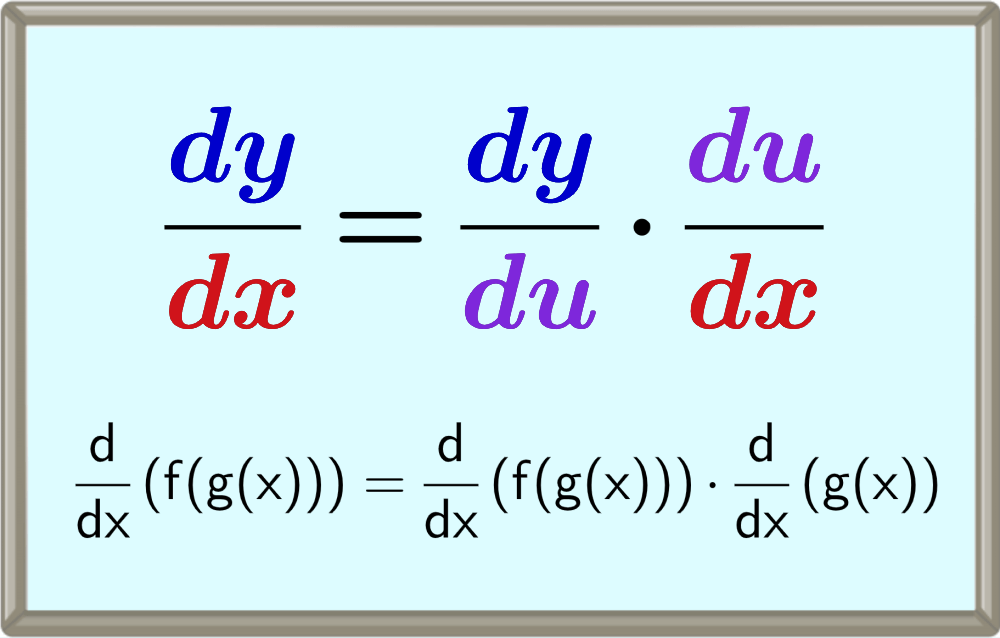Prova da Regra da Cadeia das Derivadas

O que é a regra da cadeia?

A regra da cadeia é definida como a derivada da composição de pelo menos dois tipos diferentes de funções. Esta regra pode ser usada para derivar uma composição de funções como:

$$y’ = \frac{d}{dx}[f \left( g(x) \right)]$$

onde g(x) é um domínio da função f. Nesta composição, as funções f e g devem ser dois tipos diferentes de funções, que não podem ser avaliadas algebricamente em apenas um tipo de função.

Mas como exatamente derivamos essa determinada função usando a regra da cadeia?

A regra da cadeia afirma que a derivada de uma composição de pelo menos dois tipos diferentes de funções é igual à derivada da função externa f multiplicada pela derivada de sua função interna g. A função g será o domínio da derivada da função exterior f.

Para melhor ilustrar, temos

$$\frac{d}{dx} (f(g(x))) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$

onde derivamos a função externa f usando o método da derivada da função f enquanto compomos a forma original da função g como seu domínio e então multiplicamos a quantidade total pela derivada da função interna g ou g(x).

Também podemos ilustrar a fórmula da regra da cadeia como:

$$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$$

onde

• $latex f(u) =$ a função externa
• $latex u = g(x)$, o domínio da função externa $latex f(u)$
• $latex \frac{dy}{du}=$ a derivada da função externa $latex f(u)$ em termos de $latex u$
• $latex \frac{du}{dx} =$ a derivada da função interna $latex g(x)$ em termos de $latex x$

Na maioria das vezes, esta forma de fórmula é usada para iniciantes. Embora tenha mais etapas, mostrou-se mais conveniente e menos confuso. Este formulário usa um método de substituição na fórmula da regra da cadeia para derivar as funções externas.

Algo fácil, certo? Mas não devemos tomar esta fórmula levianamente se afirmamos conseguir derivar qualquer composição de funções. Para aprender e entender os conceitos por trás do desenvolvimento desta fórmula da regra da cadeia, devemos estar familiarizados com qualquer prova que satisfaça a declaração da regra da cadeia.

Prova da regra da cadeia

Para entender esta prova, é recomendável que você esteja familiarizado com os tópicos Declive de uma reta tangente e Derivadas usando limites.

Podemos lembrar que uma derivada pode ser expressa em termos de limites da seguinte forma:

$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$

Agora suponha que temos a seguinte função:

$latex H(x) = f(g(x))$

Então, se tirarmos a derivada, temos,

$$H'(x) = \frac{d}{dx} \left( f(g(x)) \right)$$

Podemos usar a diferenciação em termos de limites:

$$H'(x) = \lim \limits_{h \to 0} {\frac{H(x+h)-H(x)}{h}}$$

Substituindo a equação $latex H(x) = f(g(x))$, temos

$$H'(x) = \lim \limits_{h \to 0} {\frac{f(g(x+h)) – f(g(x))}{h}}$$

Que manipulações podemos fazer nesse limite para chegar à fórmula da regra da cadeia?

Em nosso limite, podemos multiplicar a função por

$$\frac{g(x+h)-g(x)}{g(x+h)-g(x)}$$

que é basicamente igual a um. Portanto, isso não mudará nosso limite em nada. Ao fazer isso, temos

$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left( {\frac{f(g(x+h)) – f(g(x))}{h}} \cdot \frac{g(x+h)-g(x)}{g(x+h)-g(x)} \right)$$

Como temos um produto de duas frações em nossa equação, podemos aplicar a propriedade comutativa da multiplicação em seus denominadores. Ao fazer isso, temos

$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left( {\frac{f(g(x+h)) – f(g(x))}{g(x+h)-g(x)}} \cdot \frac{g(x+h)-g(x)}{h} \right)$$

Aplicando as propriedades dos limites, temos

$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left(\frac{f(g(x+h)) – f(g(x))}{g(x+h)-g(x)} \right) \cdot \lim \limits_{h \to 0} \left(\frac{g(x+h)-g(x)}{h} \right)$$

A segunda parte do lado direito é simplesmente a derivada de g(x) escrita em limites. Então temos

$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left(\frac{f(g(x+h)) – f(g(x))}{g(x+h)-g(x)} \right) \cdot \frac{d}{dx}(g(x))$$

Podemos usar as leis dos limites para reorganizar nosso limite assim:

$$ \frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left(\frac{1}{g(x+h)-g(x)} \right) \cdot \lim \limits_{h \to 0} \Big( f(g(x+h)) – f(g(x)) \Big) \cdot \frac{d}{dx}(g(x))$$

Marcamos esta equação como $latex EQ.01$

Mas antes de avaliarmos $latex EQ.01$, vamos usar

$latex \gamma = g(x+h)-g(x)$

Marcamos esta equação como $latex EQ.02$

Igualando $latex EQ.02$ em termos de $latex g(x+h)$, temos

$latex g(x+h) = g(x) + \gamma$

Marcamos esta equação como $latex EQ.03$

Se avaliarmos

$$\lim \limits_{h \to 0} \left( \frac{1}{g(x+h)-g(x)} \right)$$

Vamos marcar esta expressão como $latex ex.01$

de $latex EQ.01$, temos

$$\lim \limits_{h \to 0} \left( \frac{1}{g(x+h)-g(x)} \right) = \lim \limits_{h \to 0} \left( \frac{1}{\gamma} \right) $$

$$\lim \limits_{h \to 0} \left( \lim \limits_{h \to 0} \left( \frac{1}{\gamma} \right)\right) = \lim \limits_{h \to 0} \left( \lim \limits_{h \to 0} \left( \frac{1}{0} \right)\right) $$

E se avaliarmos o limite de $latex ex.01$ em termos de $latex \gamma \to 0$, temos

$$\lim \limits_{\gamma \to 0} \left( \lim \limits_{h \to 0} \left( \frac{1}{\gamma} \right) \right)= \lim \limits_{\gamma \to 0} \left( \lim \limits_{h \to 0} \left( \frac{1}{0} \right) \right)$$

Devido a isso, podemos concluir que

$latex h \to 0 = \gamma \to 0$

Portanto, agora podemos avaliar $latex EQ.01$ em termos de $latex \gamma \to 0$ em vez de $latex h \to 0$ para resolver nossos limites restantes. Então temos

$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{\gamma \to 0} \left( \frac{1}{g(x+h)-g(x)} \right) \cdot \lim \limits_{\gamma \to 0} \Big( f(g(x+h))– f(g(x)) \Big) \cdot \frac{d}{dx}(g(x))$$

Marcamos esta equação como $latex EQ.04$

Substituindo $latex EQ.02$ e $latex EQ.03$ em $latex EQ.04$, temos

$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{\gamma \to 0} \left( \frac{1}{\gamma} \right) \cdot \lim \limits_{\gamma \to 0} \Big( f(g(x) + \gamma) – f(g(x)) \Big) \cdot \frac{d}{dx}(g(x))$$

Multiplicando a equação acima, obtemos

$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{\gamma \to 0} \left( {\frac{f(g(x) + \gamma) – f(g(x))}{\gamma}} \right) \cdot \frac{d}{dx}(g(x))$$

Resolvendo o limite restante, temos

$$\frac{d}{dx} \left( f(g(x)) \right) = \frac{d}{dx} \left( f(g(x)) \right) \cdot \frac{d}{dx}(g(x))$$

ou pode ser simplesmente ilustrado como

$$H'(x) = \left( f(g(x)) \right)’ \cdot g'(x)$$

que agora é a fórmula da regra da cadeia.

Finalmente, provamos a fórmula da regra da cadeia aplicando os conceitos de limites.

Veja também

Interessado em aprender mais sobre a regra da cadeia? Dê uma olhada nessas páginas:

• Regra da Cadeia das Derivadas – Fórmula e Exemplos
• Regra da Cadeia das Derivadas – Exercícios Resolvidos
• Calculadora de derivadas