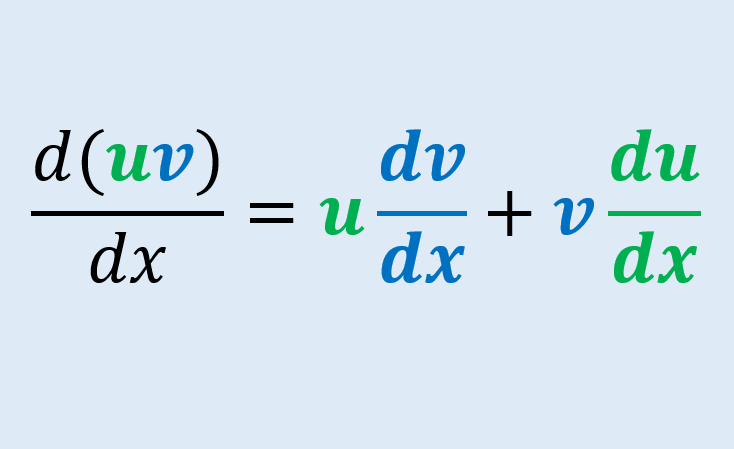Prova da Regra do Produto das Derivadas

O que é a regra do produto?

A regra do produto é definida como a derivada do produto de pelo menos duas funções. A regra do produto pode ser usada para derivar qualquer produto de funções como:

$latex (fg)'(x) = \frac{d}{dx}(f(x) \cdot g(x))$

onde f(x) e g(x) podem ser equivalentes a qualquer tipo de função.

Mas como exatamente derivamos essa função usando a regra do produto?

A regra do produto afirma que a derivada de um produto de duas funções é igual à primeira função f(x) em sua forma original multiplicada pela derivada da segunda função g(x) e adicionada à forma original da segunda função g(x) multiplicado pela derivada da primeira função f(x).

Para ilustrar melhor, quando queremos obter a derivada de fg(x) ou a derivada do produto de f(x) e g(x), temos:

$latex (fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)$

Fácil, certo? Mas não devemos tomar esta fórmula levianamente se afirmamos conseguir derivar qualquer produto de funções. Para aprender e entender os conceitos por trás do desenvolvimento desta fórmula de regra do produto, devemos estar familiarizados com qualquer prova que satisfaça a regra do produto.

Prova da regra do produto usando limites

Para esta prova, é recomendado que você se familiarize com os tópicos Declive de uma reta tangente e Derivadas usando limites, como pré-requisitos para melhor compreensão desta prova.

Podemos lembrar que

$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$

Aplicando limites, podemos derivar uma função f(x). Mas que tal um produto de duas funções f(x) e g(x)?

Por exemplo, temos duas funções f(x) e g(x) e então nos pedem para encontrar a derivada de fg(x). Ou seja, temos

$$(fg)'(x) = \frac{d}{dx}(f(x) \cdot g(x))$$

Para derivar o produto dessas duas funções usando limites, suponha que temos

$latex \Upsilon(x) = f(x) \cdot g(x)$

Então,

$$\Upsilon'(x) = \frac{d}{dx}(f(x) \cdot g(x))$$

e podemos derivar isso da seguinte forma:

$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{\Upsilon(x+h)-\Upsilon(x)}{h}}$$

Substituindo a equação $latex \Upsilon(x) = f(x) \cdot g(x)$, temos:

$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x+h) – f(x) \cdot g(x)}{h}}$$

que pode ser escrito como:

$$\frac{d}{dx}(f(x) \cdot g(x)) =\lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x+h) – f(x) \cdot g(x)}{h}}$$

Isso representa a derivada de um produto em termos de limites. Agora, essa equação não pode ser facilmente manipulada algebricamente para chegar à fórmula da regra do produto que estamos tentando provar.

No entanto, podemos adicionar e subtrair $latex f(x+h) \cdot g(x)$ ao numerador. Portanto, temos

$$\frac{d}{dx}(f(x) \cdot g(x)) =\lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x+h) – f(x+h) \cdot g(x) + f(x+h) \cdot g(x) – f(x) \cdot g(x)}{h}}$$

Como $latex + f(x+h) \cdot g(x) – f(x+h) \cdot g(x) = 0$, não alteramos a expressão.

Agora, podemos fatorar $latex f(x+h)$ dos dois primeiros termos e $latex g(x)$ dos dois últimos termos. Então, podemos dividir a expressão em duas partes e, simplificando, temos,

$$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot (g(x+h)-g(x))}{h}+\lim \limits_{h \to 0} \frac{g(x) \cdot (f(x+h)-f(x))}{h}}$$

$$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {f(x+h) \cdot \frac{g(x+h)-g(x)}{h}+\lim \limits_{h \to 0} g(x) \cdot \frac{f(x+h)-f(x)}{h}}$$

Aplicando as propriedades dos limites para resolver a equação, temos

$$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {f(x+h)} \cdot \lim \limits_{h \to 0} {\frac{g(x+h)-g(x)}{h}}+ \lim \limits_{h \to 0} {g(x)} \cdot \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$

Os limites $latex \lim \limits_{h \to 0} {f(x+h)}$ e $latex \lim \limits_{h \to 0} {g(x)}$ podem ser facilmente resolvidos. À medida que h se aproxima de zero, obteremos simplesmente $latex f(x)$ e $latex g(x)$ respectivamente.

Os limites $latex \lim \limits_{h \to 0} {\frac{g(x+h)-g(x)}{h}}$ e $latex \lim \limits_{h \to 0} {\ frac{f(x+h)-f(x)}{h}}$ parecem mais complicados, mas são simplesmente as derivadas de $latex g(x)$ e $latex h(x)$ expressas em limites. Portanto, temos:

$$\frac{d}{dx}(f(x) \cdot g(x)) = f(x) \cdot \frac{d}{dx}(g(x)) + g(x) \cdot \frac{d}{dx}(f(x))$$

ou podemos expressar isso simplesmente como

$latex (fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)$

que agora é a fórmula da regra do produto.

Prova da regra do produto usando a regra da cadeia

Este método de prova torna a regra do produto mais fácil de testar e formular. Portanto, é recomendável que você se familiarize com os tópicos A Regra da Cadeia, A Soma/Diferença das Derivadas como pré-requisito para entender melhor essa prova.

Podemos lembrar que a fórmula da regra da cadeia é

$$\frac{d}{dx}[(f(x))^n] = n \cdot (f(x))^{n-1} \cdot \frac{d}{dx}(f(x))$$

Para facilitar a derivação da regra do produto, podemos considerar a seguinte expressão:

$latex \Upsilon(x) = {{(f+g)}^2}$

onde f e g são duas funções válidas.

Vamos derivar $latex \Upsilon(x)$ usando a regra da cadeia. Portanto, temos:

$latex \Upsilon'(x)= 2(f+g)(f’+g’)$

Se multiplicarmos e expandirmos os parênteses, teremos:

$latex \Upsilon'(x)= 2(ff’+fg’+gf’+gg’)$

$latex = 2ff’+2fg’+2gf’+2gg’$

Agora, em vez de usar a regra da cadeia, podemos expandir a expressão $latex {{(f+g)}^2}$ para obter:

$latex \Upsilon(x) = {{f}^2}+fg+{{g}^2}$

Derivando termo por termo, obtemos:

$latex \Upsilon'(x)= 2ff’+2(fg)’+2gg’)$

Como as duas expressões que obtivemos para $latex \Upsilon'(x)$ são equivalentes, temos:

$$2ff’+2(fg)’+2gg’)= 2ff’+2fg’+2gf’+2gg’$$

$latex (fg)’= fg’+gf’$

Claramente chegamos à regra do produto.

Prova da regra do produto usando diferenciação logarítmica

Um terceiro método que podemos usar para provar a regra do produto é usar a diferenciação logarítmica e a diferenciação implícita. Este é um método mais rápido, mas requer que você esteja familiarizado com ambos os tópicos.

Podemos começar escrevendo a seguinte expressão:

$latex y=f(x)g(x)$

Agora, podemos tomar o logaritmo natural de ambos os lados:

$latex \ln(y)=\ln(f(x)g(x))$

Usando as leis dos logaritmos do lado direito, podemos escrever:

$latex \ln(y)=\ln f(x)+\ln g(x)$

Derivando de ambos os lados, temos:

$$\frac{y’}{y}=\frac{f'(x)}{f(x)}+\frac{g'(x)}{g(x)}$$

Resolvendo para $latex y’$, temos:

$$y’=y\left(\frac{f'(x)}{f(x)}+\frac{g'(x)}{g(x)}\right)$$

Agora, podemos substituir $latex y=f(x)g(x)$ para obter:

$$(fg)’=f(x)g(x)\left(\frac{f'(x)}{f(x)}+\frac{g'(x)}{g(x)}\right)$$

Se multiplicarmos e expandirmos os parênteses, teremos:

$latex (fg)’=g(x)f'(x)+f(x)g'(x)$

Chegamos à regra do produto.

Veja também

Interessado em saber mais sobre a regra do produto? Dê uma olhada nessas páginas:

• Regra do Produto das Derivadas – Fórmula e Exemplos
• Regra do Produto das Derivadas – Exercícios Resolvidos
• Calculadora de derivadas