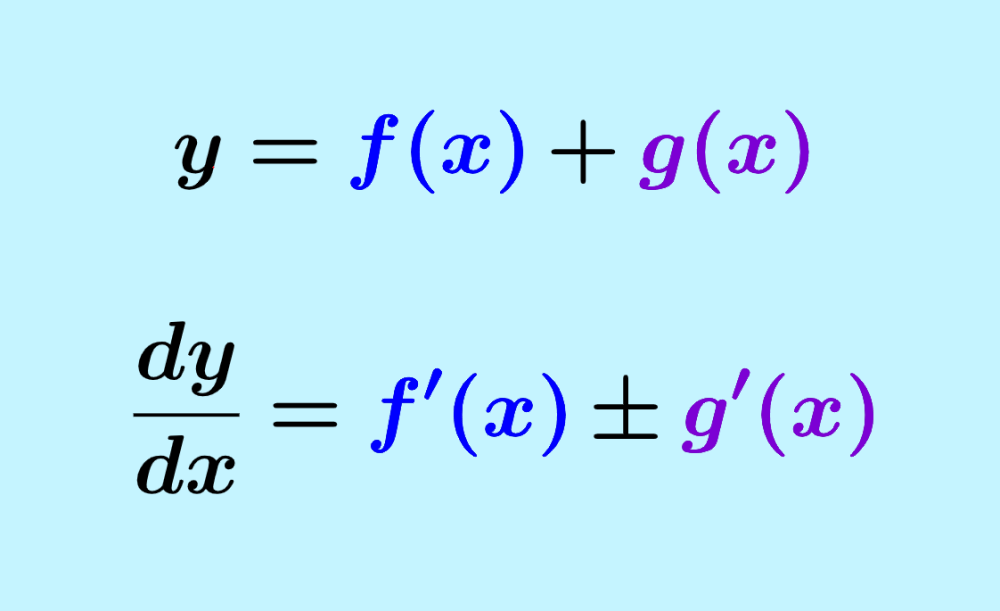Para derivar uma adição ou subtração de funções, temos que diferenciar cada termo da função separadamente. Isso significa que podemos simplesmente aplicar a regra da potência ou outra regra relevante para diferenciar cada termo e encontrar a derivada de toda a função.
A seguir, vamos resolver 10 exercícios sobre derivadas da adição e subtração de funções. Além disso, exploraremos problemas para praticar a diferenciação dessas funções.
CÁLCULO
Relevante para…
Resolver exercícios de derivadas de adição e subtração de funções.
CÁLCULO
Relevante para…
Resolver exercícios de derivadas de adição e subtração de funções.
Definição e fórmula da regra de adição e subtração de funções em derivadas
A regra para derivadas de adição ou subtração de funções nos diz que quando $latex y$ é composto por mais de uma função, podemos encontrar sua derivada diferenciando cada função uma a uma.
A regra de adição e subtração de funções em derivadas nos permite encontrar a derivada de funções como as seguintes:
$latex y=f(x)+g(x)$
Então, sua derivada é igual a:
$$\frac{dy}{dx}=f'(x) \pm g'(x)$$
Isso se aplica à soma ou diferença de qualquer número de funções.
Para derivar cada uma das funções ou cada um dos termos, usamos a regra da potência, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, ou qualquer outra regra de derivada aplicável.
Passos para derivar uma adição ou subtração de duas ou mais funções
Suponha que temos que derivar
$latex f(x) = x^2+5x$
Temos uma função que é uma adição de dois termos. Assim, podemos derivar seguindo estes passos:
1. Use as leis dos expoentes para transformar radicais ou expressões racionais para forma exponencial.
Neste caso, não temos radicais ou expressões racionais. Nota: Um exemplo seria escrever $latex \sqrt{x}$ como $latex x^{\frac{1}{2}}$.
2. Aplique a fórmula da regra de potência, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, ou outras regras aplicáveis a cada termo na adição ou subtração:
$$f'(x) = 2x+5$$
3. Simplifique a expressão resultante.
Nesse caso, não podemos mais simplificar. Nota: Um exemplo seria escrever $latex x^{-\frac{1}{2}}$ como $latex \frac{1}{\sqrt{x}}$.
Você pode usar $latex f'(x), y’,$ ou $latex \frac{d}{dx}(f(x))$ como o símbolo da derivada no lado esquerdo da resposta final.
Exercícios resolvidos de derivadas de adição e subtração de funções
EXERCÍCIO 1
Encontre a derivada de $latex f(x)=x^4+5x$.
Solução
Passo 1: Começamos convertendo expressões radicais ou racionais para sua forma exponencial. Neste caso, não temos radicais nem variáveis escritas na forma racional.
Passo 2: Usamos a fórmula da regra da potência, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, para diferenciar os dois termos da função:
$latex f(x)=x^4+5x$
$latex f'(x)=4(x^{4-1})+5(x^{1-1})$
$latex f'(x)=4x^3+5$
Passo 3: Simplificamos se possível. Neste caso, não.
EXERCÍCIO 2
Qual é a derivada da função $latex f(x)=-5x^3+10x^2$?
Solução
Passo 1: A função não tem radicais ou expressões racionais.
Passo 2: Vamos derivar usando a regra da potência, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, para derivar os dois termos da função:
$latex f(x)=-5x^3+10x^2$
$latex f(x)=3(-5x^{3-1})+2(10x^{2-1})$
$latex f'(x)=-15x^2+20x$
Passo 3: A função agora está simplificada.
EXERCÍCIO 3
Encontre a derivada da função $latex f(x)=7x^8+5x^{-3}$.
Solução
Passo 1: Ambos os termos possuem variáveis com expoentes numéricos.
Passo 2: Temos um expoente negativo, mas simplesmente usamos a regra da potência para derivar os dois termos:
$latex f(x)=7x^8+5x^{-3}$
$latex f(x)=8(7x^{8-1})+(-3)(5x^{-3-1})$
$latex f'(x)=56x^7-15x^{-4}$
Passo 3: Usando as leis dos expoentes, podemos escrever da seguinte forma:
$$f'(x)=56x^7-\frac{15}{x^4}$$
EXERCÍCIO 4
Encontre a derivada da função $latex f(x)=3x^{-5}-2x^{-2}$.
Solução
Passo 1: Temos expoentes negativos, mas não há radicais ou variáveis com expressões racionais.
Passo 2: Usamos a fórmula da regra da potência, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, para diferenciar os dois termos da função:
$latex f(x)=3x^{-5}-2x^{-2}$
$latex f(x)=-5(3x^{-5-1})-2(-2x^{-2-1})$
$latex f'(x)=-15x^{-6}+4x^{-3}$
Passo 3: Usamos as leis dos expoentes para simplificar:
$$f'(x)=-\frac{15}{x^6}+\frac{4}{x^3}$$
EXERCÍCIO 5
Qual é a derivada da função $latex f(x)=-5x^4+ \frac{1}{x}$?
Solução
Passo 1: Usando as leis dos expoentes, podemos escrever da seguinte forma:
$latex f(x)=-5x^4+ x^{-1}$
Passo 2: Agora que temos apenas expoentes numéricos, usamos a fórmula da regra da potência, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, em ambos os termos da função:
$latex f(x)=-5x^4+ x^{-1}$
$latex f'(x)=-20x^3-x^{-2}$
Passo 3: Com as leis dos expoentes, podemos escrever da seguinte forma:
$$f'(x)=-20x^3-\frac{1}{x^2}$$
EXERCÍCIO 6
Qual é a derivada de $latex f(x)=4x^3+2x^2+\frac{2}{x^3}$?
Solução
Passo 1: Começamos convertendo a expressão racional para uma expressão com um expoente numérico:
$latex f(x)=4x^3+2x^2+2x^{-3}$
Passo 2: Usando a regra da potência para os três termos, temos:
$latex f(x)=4x^3+2x^2+2x^{-3}$
$latex f'(x)=12x^2+4x-6x^{-4}$
Passo 3: Usamos as leis dos expoentes novamente para escrever da seguinte forma:
$$f'(x)=12x^2+4x-\frac{6}{x^4}$$
EXERCÍCIO 7
Determine a derivada de $latex f(x)=3x^2+\frac{2}{3x^2}+ x^{ \frac{1}{2}}$.
Solução
Passo 1: Usamos as leis dos expoentes para escrever a função assim:
$$f(x)=3x^2+\frac{2}{3}x^{-2}+ x^{-\frac{1}{2}}$$
Passo 2: Usando a regra da potência nos três termos da função, temos:
$$f(x)=3x^2+\frac{2}{3}x^{-2}+ x^{-\frac{1}{2}}$$
$$f'(x)=6x-\frac{4}{3}x^{-3}-\frac{1}{2}x^{-\frac{3}{2}}$$
Passo 3: Simplificamos escrevendo da seguinte forma:
$$f'(x)=6x-\frac{4}{3x^3}-\frac{1}{2x^{\frac{3}{2}}}$$
$$f'(x)=6x-\frac{4}{3x^3}-\frac{1}{2\sqrt{x^3}}$$
EXERCÍCIO 8
Encontre a derivada da função $latex f(x)=\sqrt{x}+ \frac{3}{x^3} $.
Solução
Passo 1: Aplicando as leis dos expoentes, podemos escrever da seguinte forma:
$$f(x)=x^{\frac{1}{2}}+3x^{-3}$$
Passo 2: Aplicamos a regra da potência para derivar ambos os termos:
$$f(x)=x^{\frac{1}{2}}+3x^{-3}$$
$$f'(x)=\frac{1}{2}x^{-\frac{1}{2}}-9x^{-4}$$
Passo 3: Usando as leis dos expoentes novamente, podemos escrever da seguinte forma:
$$f'(x)=\frac{1}{2x^{\frac{1}{2}}}-\frac{9}{x^4}$$
$$f'(x)=\frac{1}{2\sqrt{x}}-\frac{9}{x^4}$$
EXERCÍCIO 9
Encontre a derivada de $latex f(x)=5x^{-5}+\frac{1}{\sqrt{x}}$.
Solução
Passo 1: Começamos escrevendo da seguinte forma:
$$f(x)=5x^{-5}+x^{-\frac{1}{2}}$$
Passo 2: Derivando ambos os termos com a regra da potência, temos:
$$f(x)=5x^{-5}+x^{-\frac{1}{2}}$$
$$f'(x)=-25x^{-6}-\frac{1}{2}x^{-\frac{3}{2}}$$
Passo 3: Simplificamos a expressão resultante usando as leis dos expoentes:
$$f'(x)=-\frac{25}{x^6}-\frac{1}{2x^{\frac{3}{2}}}$$
$$f'(x)=-\frac{25}{x^6}-\frac{1}{2\sqrt{x^3}}$$
EXERCÍCIO 10
Encontre a derivada de $latex f(x)=\frac{2}{3x^2}+ \frac{1}{\sqrt[3]{x^2}}- \frac{5}{x}$.
Solução
Passo 1: Começamos usando as leis dos expoentes para escrever assim:
$$f(x)=\frac{2}{3}x^{-2}+ x^{\frac{2}{3}}- 5x^{-1}$$
Passo 2: Usamos a regra da potência para derivar os termos:
$$f(x)=\frac{2}{3}x^{-2}+ x^{-\frac{2}{3}}- 5x^{-1}$$
$$f'(x)=-\frac{4}{3}x^{-3}- \frac{2}{3}x^{-\frac{5}{3}}+ 5x^{-2}$$
Passo 3: Finalmente, simplificamos da seguinte forma:
$$f'(x)=-\frac{4}{3x^3}- \frac{2}{3x^{\frac{5}{3}}}+ \frac{5}{x^2}$$
$$f'(x)=-\frac{4}{3x^3}- \frac{2}{3\sqrt[3]{x^5}}+ \frac{5}{x^2}$$
Exercícios de derivadas de adição e subtração de funções para resolver
Encontre o valor de $latex f'(5)$ se tivermos a seguinte função: $$f(x)=4x^3-6x^2+3x-10$$
Escreva o resultado na caixa.
Veja também
Interessado em aprender mais sobre derivadas? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
