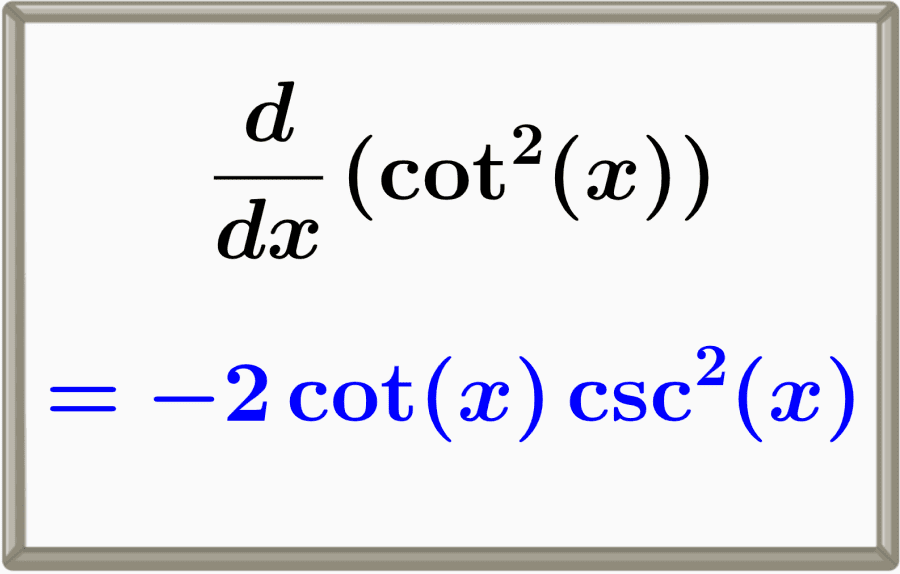A derivada da cotangente ao quadrado é igual a menos dois cotangente multiplicado pela cossecante ao quadrado, -2cot(x)csc2(x). Esta derivada pode ser encontrada usando a regra da cadeia e as derivadas das funções trigonométricas fundamentais.
Aqui, aprenderemos como provar esta derivada, veremos uma comparação gráfica da cotangente quadrado e da sua derivada e resolveremos alguns exercícios.
Prova da derivada da cotangente ao quadrado usando a regra da cadeia
Como pré-requisito, você pode revisar a fórmula da regra da cadeia e sua prova consultando este artigo: Regra da cadeia. Da mesma forma, você pode revisar a prova da derivada da função cotangente visitando este artigo: Derivada da Cotangente, cot(x).
Vamos lembrar disso
$latex \cot^{2}{(x)} \neq \cot{(x^2)}$
Por ser uma função composta, a fórmula da regra da cadeia é usada como uma ferramenta mais direta para provar a derivada da função cotangente ao quadrado.
Então, começamos com a função:
$latex F(x) = \cot^{2}{(x)}$
Para uma melhor representação, podemos reescrever como
$latex F(x) = \cot^{2}{(x)}$
$latex F(x) = (\cot{(x)})^2$
É evidente que a função potência dada é a função externa a ser considerada, enquanto a função cotangente, sendo elevada pela função potência dada, é a função interna. Podemos configurar a função externa da seguinte forma:
$latex f(u) = u^2$
onde
$latex u = \cot{(x)}$
A função cotangente trigonométrica, como função interna de f(u), será denotada como g(x).
$latex f(u) = f(g(x))$
$latex u = g(x)$
$latex g(x) = \cot{(x)}$
Derivando a função externa f(u) usando a regra da potência em termos de u, temos
$latex f(u) = u^2$
$latex f'(u) = 2u$
Derivando a função interna g(x) usando a fórmula derivada da função trigonométrica cotangente em termos de x, temos
$latex g(x) = \cot{(x)}$
$latex g'(x) = -\csc^{2}{(x)}$
Multiplicando algebricamente a derivada da função externa $latex f'(u)$ pela derivada da função interna $latex g'(x)$, temos
$latex \frac{dy}{dx} = f'(u) \cdot g'(x)$
$latex \frac{dy}{dx} = (2u) \cdot (-\csc^{2}{(x)})$
Substituindo u em f‘(u), temos
$latex \frac{dy}{dx} = (2(\cot{(x)})) \cdot (-\csc^{2}{(x)})$
$latex \frac{dy}{dx} = – 2\cot{(x)} \cdot \csc^{2}{(x)}$
o que nos leva à fórmula da derivada da cossecante ao quadrado x
$latex \frac{d}{dx} \cot^{2}{(x)} = -2\cot{(x)}\csc^{2}{(x)}$
Por que a derivada da cotangente quadrado e a cossecante quadrado são iguais?
Você pode estar se perguntando por que a derivada de ambas as funções
$latex \cot^{2}{(x)}$
e
$latex \csc^{2}{(x)}$
são as mesmas.
A identidade trigonométrica pitagórica para cotangentes e cossecantes nos diz que
$latex \csc^{2}{(x)} = 1 + \cot^{2}{(x)}$
Se derivarmos ambos os lados desta fórmula, temos:
$latex \frac{d}{dx} (\csc^{2}{(x)}) = \frac{d}{dx}(1) + \frac{d}{dx}(\cot^{2}{(x)})$
Agora, vemos que no lado direito temos uma derivada de uma constante, que é igual a zero. Então,
$latex \frac{d}{dx} (\csc^{2}{(x)}) = 0 + \frac{d}{dx}(\cot^{2}{(x)})$
$latex \frac{d}{dx} (\csc^{2}{(x)}) = \frac{d}{dx}(\cot^{2}{(x)})$
É por isso que tanto a cotangente ao quadrado quanto a cossecante ao quadrado têm a mesma derivada.
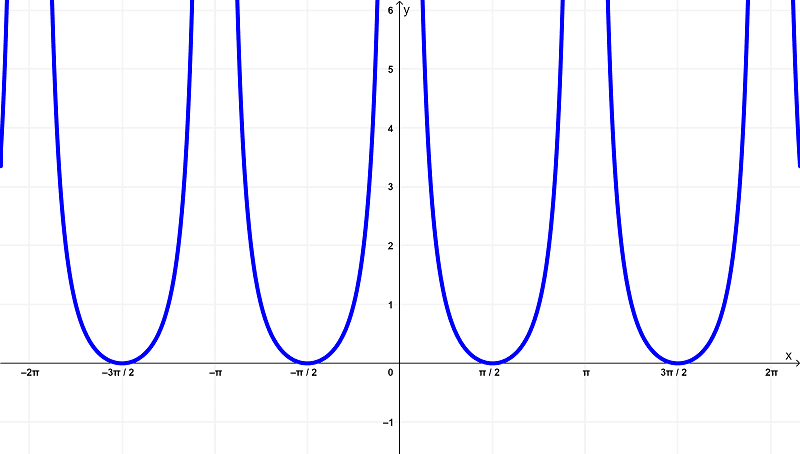
Gráfico de cotangente quadrado x VS. a derivada da cotangente ao quadrado x
O gráfico da
$latex f(x) = \cot^{2}{(x)}$
é
Diferenciando para a função $latex f(x) = \cot^{2}{(x)}$, temos
$latex f'(x) = -2\cot{(x)}\csc^{2}{(x)}$
seu gráfico é
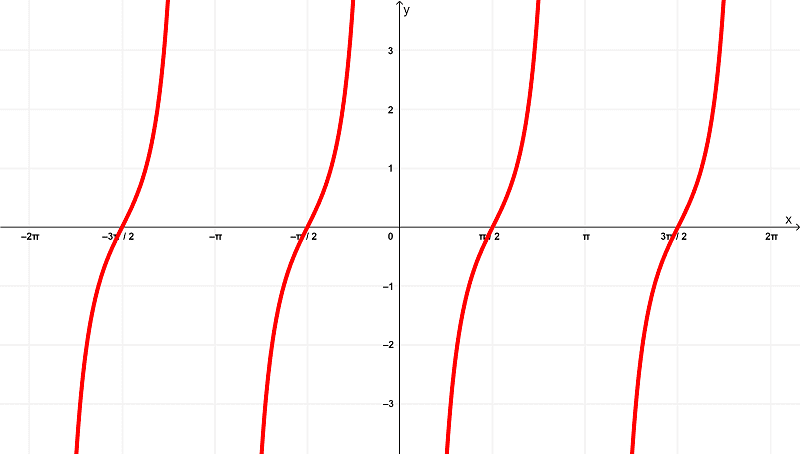
Comparando seus gráficos, temos:
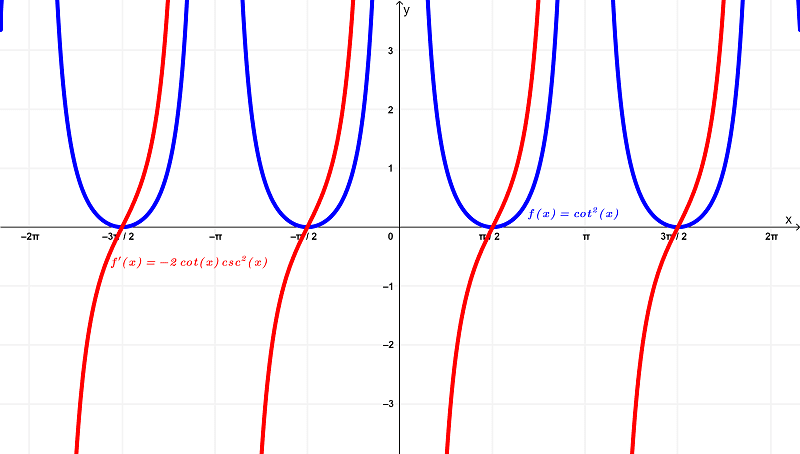
Usando seus gráficos, vemos que a função original $latex f(x) = \cot^{2}{(x)}$ tem um domínio de
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
dentro dos intervalos finitos de
$latex (-2\pi,2\pi)$
e está dentro da imagem de
$latex [0,\infty)$
enquanto a derivada $latex f'(x) = -2\cot{(x)}\csc^{2}{(x)}$ tem um domínio de
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
dentro dos intervalos finitos de
$latex (-2\pi,2\pi)$
e está dentro da imagem de
$latex (-\infty,\infty)$
Exemplos
Os exemplos seguintes mostram como encontrar a derivada da cotangente quadrado composta.
EXEMPLO 1
Determine a derivada da função $latex f(x) = \cot^2(7x)$.
Solução
Para derivar esta função, temos de utilizar a regra da cadeia, uma vez que se trata de uma função cotangente quadrado composta.
Então, se considerarmos $latex u=7x$ como a função interna, podemos escrever $latex f(u)=\cot^2(u)$. Usando a regra da cadeia, temos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-2\cot(u)\csc^2(u) \times 7$$
Agora, substituímos $latex u=7x$ de volta à função e temos:
$$\frac{dy}{dx}=-14\cot(7x)\csc^2(7x)$$
EXEMPLO 2
Qual é a derivada da função $latex F(x) = \cot^2(3x^3-5x)$?
Solução
Aqui, a função interna é $latex u=3x^3-5x$. Assim, a função externa é $latex f (u) = \cot^2(u)$.
Agora, começamos por encontrar a derivada da função externa:
$$\frac{d}{du} ( \cot^2(u) ) = -2\cot(u)\csc^2(u)$$
A seguir, encontramos a derivada da função interior e temos:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(3x^3-5x)$$
$$\frac{d}{dx}(g(x)) = 9x^2-5$$
Pela regra da cadeia, multiplicamos a derivada de $latex f(u)$ pela derivada de $latex g(x)$ e temos:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = -2\cot(u)\csc^2(u) \cdot (9x^2-5)$$
Finalmente, aplicamos a substituição $latex u=3x^3-5x$ e simplificamos:
$$\frac{dy}{dx} = -2\cot(3x^3-5x)\csc^2(3x^3-5x) \cdot (9x^2-5)$$
$$\frac{dy}{dx} = -(18x^2-10)\cot(3x^3-5x)\csc^2(3x^3-5x)$$
Prática de derivadas de funções cotangente quadrado
Veja também
Interessado em aprender mais sobre derivadas de funções trigonométricas ao quadrado? Veja estas páginas:
- Derivada de cosseno quadrado, cos^2(x) – Demonstração e gráficos
- Derivada de seno quadrado, seno^2(x) – Demonstração e gráficos
- Derivada de tangente quadrado, tan^2(x) – Demonstração e gráficos
- Derivada da secante quadrado, sec^2(x) – Demonstração e gráficos
- Derivada de cossecante quadrado, csc^2(x) – Demonstração e gráficos
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
