A derivada da função cotangente é igual a menos cossecante ao quadrado, -csc²(x). Esta derivada pode ser provada usando limites e identidades trigonométricas.
Neste artigo, vamos aprender como derivar a função trigonométrica cotangente. Veremos como provar esta derivada, uma comparação gráfica de cotangente e alguns exemplos.
Prova da derivada da função cotangente
A função trigonométrica cotangente de um ângulo é definida como a razão entre o lado adjacente e o lado oposto de um ângulo em um triângulo retângulo. Ilustrando-o através de uma figura, temos
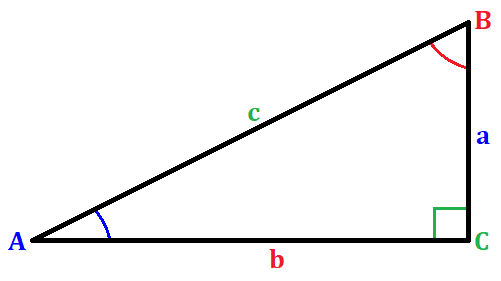
onde C é 90°. Para o triângulo retângulo da amostra, a obtenção da cotangente do ângulo A pode ser avaliada como
$latex \cot{(A)} = \frac{b}{a}$
onde A é o ângulo, b é o lado adjacente e a é o lado oposto.
Antes de aprender a prova da derivada da função cotangente, recomenda-se aprender o teorema de Pitágoras, Soh-Cah-Toa & Cho-Sha-Cao, e o princípio dos limites como pré-requisitos.
Para revisar, qualquer função pode ser diferenciada definindo-a igual ao limite de
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Suponha que temos que encontrar a derivada de
$latex f(x) = \cot{(x)}$
então temos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cot{(x+h)} – \cot{(x)} }{h}}$$
Analisando nossa equação, podemos ver que tanto o primeiro quanto o segundo termos no numerador do limite são cotangentes de uma soma de dois ângulos x e h e uma cotangente do ângulo x. Com essa observação, podemos tentar aplicar as identidades de relacionamento definidoras para cotangente, cosseno e seno. Aplicando isso, temos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \frac{\cos{(x+h)}}{\sin{(x+h)}} – \frac{\cos{(x)}}{\sin{(x)}} }{h}}$$
Reorganizando algebricamente aplicando algumas regras de fração, temos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \frac{\cos{(x+h)}\sin{(x)} – \sin{(x+h)}\cos{(x)}}{\sin{(x+h)}\sin{(x)}} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x)}\cos{(x+h)} – \cos{(x)}\sin{(x+h)} }{h\sin{(x+h)}\sin{(x)}}}$$
Observando o numerador rearranjado, podemos tentar aplicar as identidades de soma e diferença para seno e cosseno, também chamadas de identidades ptolomaicas.
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x-(x+h))} }{h\sin{(x+h)}\sin{(x)}}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x-x-h)} }{h\sin{(x+h)}\sin{(x)}}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(-h)} }{h\sin{(x+h)}\sin{(x)}}}$$
Com base nas identidades trigonométricas de um seno de um ângulo negativo, é igual ao seno negativo desse mesmo ângulo, mas na forma positiva. Aplicando isso ao nosso numerador, temos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ -\sin{(h)} }{h\sin{(x+h)}\sin{(x)}}}$$
Reorganizando aplicando o limite do produto de duas funções, temos
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ \sin{(h)} }{h} \cdot \frac{-1}{\sin{(x+h)}\sin{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ \sin{(h)} }{h} \cdot \left(-\frac{1}{\sin{(x+h)}\sin{(x)}}\right) \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ \sin{(h)} }{h} \right)} \cdot \lim \limits_{h \to 0} {\left(-\frac{1}{\sin{(x+h)}\sin{(x)}} \right)}$$
De acordo com os limites das funções trigonométricas, o limite da função trigonométrica $latex \sin{(\theta)}$ para $latex \theta$ quando $latex \theta$ se aproxima de zero é igual a um. O mesmo pode ser aplicado a $latex \sin{(h)}$ sobre $latex h$. Aplicando temos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {1} \cdot \lim \limits_{h \to 0} {\left(-\frac{1}{\sin{(x+h)}\sin{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left(-\frac{1}{\sin{(x+h)}\sin{(x)}} \right)}$$
Finalmente, avaliamos o limite do que resta na equação. Substituindo o valor aproximado de $latex por h$, temos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left(-\frac{1}{\sin{(x+h)}\sin{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left(-\frac{1}{\sin{(x+(0))}\sin{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left(-\frac{1}{\sin{(x)}\sin{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = -\frac{1}{\sin{(x)}\sin{(x)}}$$
Sabemos pelas identidades recíprocas que a função trigonométrica recíproca do seno é cossecante. Aplicando, temos
$$\frac{d}{dx} f(x) = – \left( \frac{1}{\sin{(x)}} \cdot \frac{1}{\sin{(x)}} \right)$$
$$\frac{d}{dx} f(x) = – (\csc{(x)} \cdot \csc{(x)})$$
$$\frac{d}{dx} f(x) = -(\csc^{2}{(x)})$$
$$ \frac{d}{dx} f(x) = -\csc^{2}{(x)}$$
Portanto, a derivada da função trigonométrica ‘cotangente’ é:
$$\frac{d}{dx} (\cot{(x)}) = -\csc^{2}{(x)}$$
Gráfico da cotangente de x vs. a derivada da cotangente de x
Dada a função
$latex f(x) = \cot{(x)}$
seu gráfico é
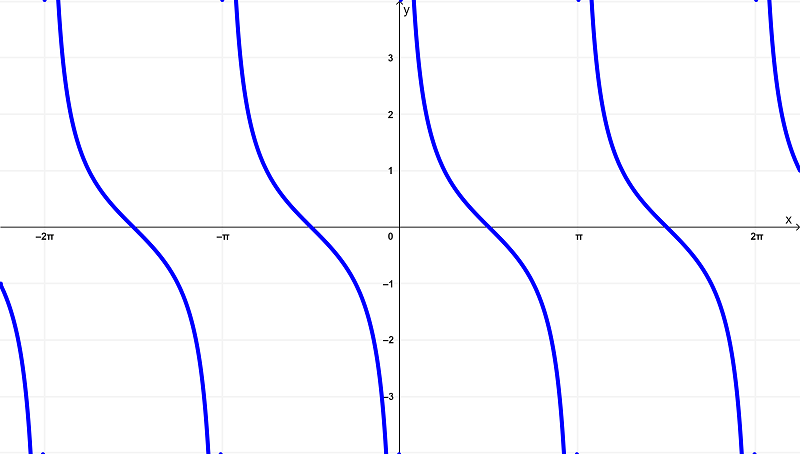
Derivando para a função $latex f(x) = \cot{(x)}$, obtemos
$latex f'(x) = -\csc^{2}{(x)}$
e seu gráfico é
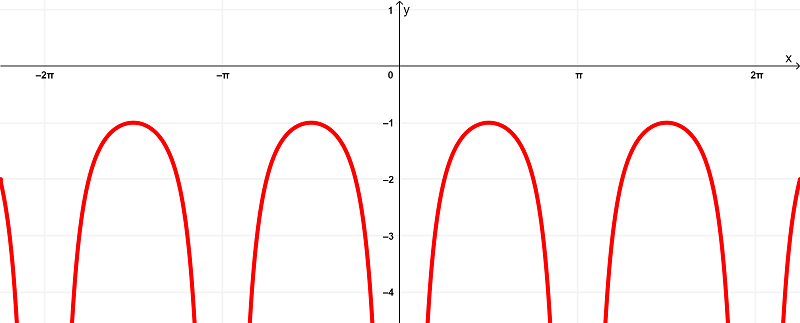
Comparando seus gráficos, temos
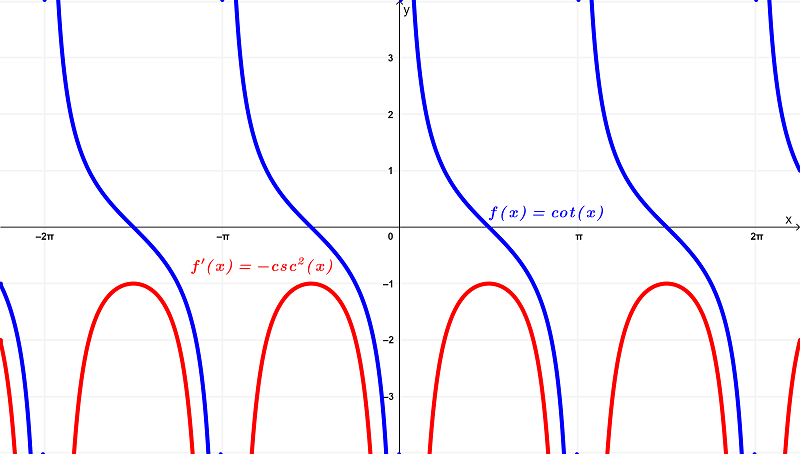
Analisando as diferenças dessas funções nesses gráficos, você vemos que a função original $latex f(x) = \cot{(x)}$ tem domínio de
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
dentro dos intervalos finitos de
$latex (-2\pi,2\pi)$
e existe dentro da imagem de
$latex (-\infty,\infty)$ ou todos os números reais
enquanto a derivada $latex f'(x) = -\csc^{2}{(x)}$ tem domínio de
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
dentro dos intervalos finitos de
$latex (-2\pi,2\pi)$
e existe dentro da imagem de
$latex (-\infty,-1]$ or $latex y \leq -1$
Exemplos
Abaixo estão alguns exemplos de como derivar uma função cotangente composta.
EXEMPLO 1
Qual é a derivada de $latex f(x) = \cot(9x)$?
Solução
Para derivar esta função, consideramos que temos uma função composta, pois a cotangente é aplicada a $latex 9x$.
Considerando $latex u=9x$ como função interna, temos $latex f(u)=\cot(u)$ e usando a regra da cadeia, temos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\csc^2(u) \times 9$$
Por fim, substituímos $latex u=9x$ de volta na função e temos:
$$\frac{dy}{dx}=-9\csc^2(9x)$$
EXEMPLO 2
Derivar a função $latex F(x) = \cot(7x^2-7)$
Solução
Esta função pode ser derivada usando a regra da cadeia porque é uma função composta cotangente.
Então, vamos começar escrevendo a função cotangente como $latex f (u) = \cot(u)$, onde $latex u = 7x^2-7$.
Agora, vamos encontrar a derivada da função externa $latex f(u)=\cot(u)$:
$$\frac{d}{du} ( \cot(u) ) = -\csc^2(u)$$
Depois, encontramos a derivada da função interna $latex u=g(x)=7x^2-7$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(7x^2-7)$$
$$\frac{d}{dx}(g(x)) = 14x$$
Para usar a regra da cadeia, multiplicamos a derivada da função externa pela derivada da função interna:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = -\csc^2(u) \cdot 14x$$
Finalmente, substituímos $latex u=7x^2-7$ de volta:
$$\frac{dy}{dx} = -\csc^2(7x^2-7) \cdot 14x$$
$$\frac{dy}{dx} = -14x\csc^2(7x^2-7)$$
EXEMPLO 3
Encontre a derivada de $latex f(x) = \cot(\sqrt{x})$
Solução
Para derivar esta função, usamos a regra da cadeia e consideramos $latex u=\sqrt{x}$ como a função interna.
Assim, podemos encontrar a derivada $latex \frac{du}{dx}$ escrevendo $latex u=\sqrt{x}$ como $latex u=x^{\frac{1}{2}}$:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Agora, consideramos que $latex f(u)=\cot(u)$ e usamos a regra da cadeia:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\csc^2(u) \times \frac{1}{2}x^{-\frac{1}{2}}$$
Substituindo $latex u=\sqrt{x}$ de volta e simplificando, temos:
$$\frac{dy}{dx}=-\csc^2(\sqrt{x}) \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=-\frac{1}{2\sqrt{x}}\csc^2(\sqrt{x})$$
Prática de derivadas de funções cotangentes compostas
Veja também
Interessado em aprender mais sobre derivadas de funções trigonométricas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
