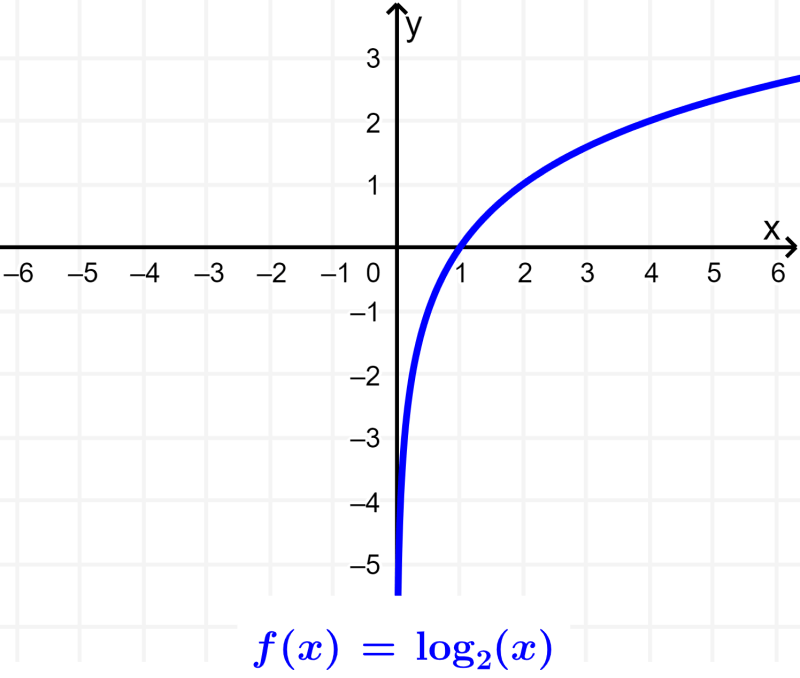
Existem várias aplicações de funções logarítmicas na vida cotidiana. As funções logarítmicas nos permitem modelar certas situações da vida real. Por exemplo, podemos usar escalas logarítmicas para medir intensidades de terremotos (escala de Ritcher) e para criar a escala de decibéis do som e a escala de pH. Também podemos obter modelos para solução tampão e entropia de informação.
Aplicações importantes de funções logarítmicas
As funções logarítmicas têm aplicações em diversas áreas. A seguir estão alguns dos mais importantes:
Álgebra e Cálculo
As funções logarítmicas são usadas em cálculo para resolver problemas envolvendo crescimento e decaimento exponencial. Por exemplo, elas podem ser usadas para encontrar a taxa instantânea de variação de uma função ou para resolver equações diferenciais envolvendo funções exponenciais.
Física
As funções logarítmicas descrevem fenômenos como intensidade do som e terremotos. Por exemplo, a escala de decibéis, que é usada para medir a intensidade do som, é baseada em uma função logarítmica.
Em sismologia, a escala Richter, que mede a magnitude dos terremotos, também se baseia em uma função logarítmica.
Engenharia
As funções logarítmicas são usadas para projetar e analisar circuitos eletrônicos, sistemas de controle e sistemas mecânicos. Por exemplo, na engenharia eletrônica, as funções logarítmicas são usadas para projetar e analisar amplificadores, filtros e osciladores.
Em sistemas de controle, as funções logarítmicas são usadas para modelar o comportamento do sistema e projetar controladores.
Na engenharia mecânica, as funções logarítmicas são usadas para analisar o comportamento de estruturas e projetar sistemas mecânicos.
Informática
Na ciência da computação, as funções logarítmicas ajudam na análise de algoritmos e no projeto de algoritmos eficientes. Um exemplo é a análise da complexidade temporal e espacial dos algoritmos.
Muitos algoritmos, como a pesquisa binária e o algoritmo quicksort, têm complexidade de tempo logarítmica, tornando-os altamente eficientes para grandes conjuntos de dados.
Economia
O crescimento econômico pode ser analisado com funções logarítmicas e isso permite analisar as tendências do mercado. Por exemplo, eles são usados para modelar o crescimento do PIB e a propagação da inflação.
Química
As funções logarítmicas podem ser usadas para descrever o comportamento das reações químicas. Por exemplo, eles são usados para descrever a taxa de reações químicas, a qual é geralmente medida em termos da mudança na concentração de um reagente ou produto ao longo do tempo.
Astronomia
As funções logarítmicas nos permitem descrever o brilho das estrelas e a distância das galáxias. Por exemplo, a escala de magnitude, que é usada para medir o brilho das estrelas, é baseada em uma função logarítmica.
As funções logarítmicas também são usadas para estimar a distância das galáxias, que podem ser muito grandes.
Meteorologia
Com o uso de funções logarítmicas, é possível descrever o comportamento da pressão atmosférica e da temperatura. Por exemplo, essas funções são usadas para modelar o comportamento da pressão atmosférica e da temperatura em diferentes altitudes.
Magnitude de um terremoto
Uma das aplicações das funções logarítmicas é a medição de intensidades de terremotos (escala de Ritcher), som (decibéis) e bases e ácidos (pH). Vamos analisar a medição da intensidade do terremoto.
Em 1935, Charles Ritcher definiu a magnitude de um terremoto com a fórmula:
$latex M=\log \left( \frac{I}{S}\right)$
onde I é a intensidade do terremoto medida pela amplitude de um sismômetro tomado 100 km do epicentro e S é a intensidade de um terremoto padrão, que é definido com uma amplitude de 1 micrômetro ou $latex {{10}^{- 4 }}$ cm.
Isso significa que a magnitude de um terremoto padrão é:
$latex M=\log \left( \frac{S}{S}\right)=\log (1)=0$
Um dos maiores terremotos já registrados teve uma magnitude de 8,9 na escala de Ritcher. Isso seria equivalente a uma intensidade de 800 milhões, então a escala de Ritcher nos permite obter números mais gerenciáveis.
Cada aumento de um número na escala de Ritcher indica um aumento de 10 vezes na intensidade. Por exemplo, um terremoto de magnitude 6 é dez vezes mais forte do que um terremoto de magnitude 5. Um terremoto de magnitude 8 é 100 vezes mais forte do que um terremoto de magnitude 6.
EXEMPLO
Na virada do século, um terremoto na Califórnia registrou 8,3 na escala de Ritcher. No mesmo ano, outro terremoto foi registrado na América do Sul, que foi 4 vezes mais forte. Qual foi a magnitude do terremoto registrado na América do Sul?
Solução: Formamos uma equação com os dados fornecidos na primeira frase:
$latex M_{C}=\log \left( \frac{I_{C}}{S}\right)=8.3$
$latex 8.3=\log \left( \frac{I_{C}}{S}\right)$
Agora, usamos os dados da segunda frase para formar a segunda equação:
$latex M_{SA}=\log \left( \frac{I_{SA}}{S}\right)$
$latex M_{SA}=\log \left( \frac{4I_{C}}{S}\right)$
Agora, resolvemos para $latex M_{SA}$:
$latex M_{SA}=\log \left( \frac{4I_{C}}{S}\right)$
$latex =\log (4I_{C})-\log (S)$
$latex =\log (4)+\log (I_{C})-\log (S)$
$latex =\log (4)+(\log (I_{C})-\log (S))$
$latex =\log (4)+\frac{\log (I_{C})}{\log (S)}$
$latex =\log (4)+8.3$
$latex =0.602+8.3$
$latex =8.902$
$latex M_{SA}=8.9$
Portanto, a intensidade do terremoto na América do Sul foi de 8,9 na escala de Ritcher.
Solução tampão
Os sistemas químicos conhecidos como soluções tampão ou tampões químicos têm a capacidade de se adaptar a pequenas mudanças na acidez para manter uma faixa de valores de pH. As soluções tampão têm uma ampla variedade de aplicações, desde a manutenção do aquário até a regulação dos níveis de pH no sangue.
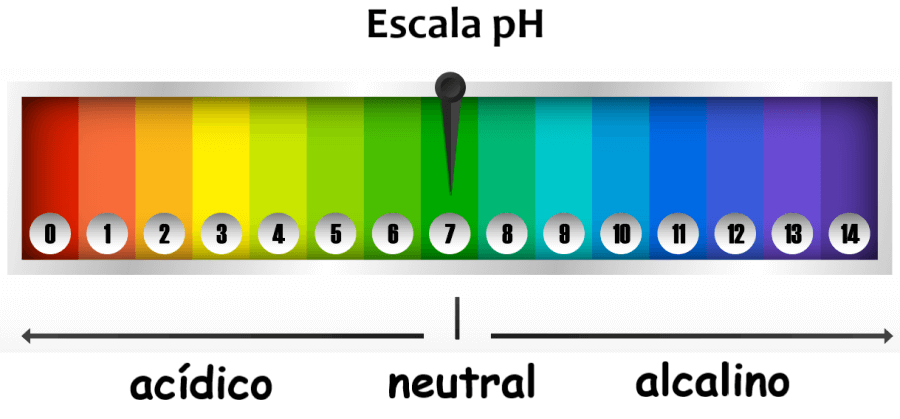
EXEMPLO
O sangue é uma solução tampão. Quando o dióxido de carbono é absorvido pelas correntes sanguíneas, ele produz ácido carbônico e reduz os níveis de pH. O corpo compensa produzindo bicarbonato, que é uma base fraca, para neutralizar o ácido. A equação de Henderson-Hasselbalch pode ser usada para calcular o pH de uma solução tampão.
Hasselbalch estava estudando o dióxido de carbono que se dissolve no sangue e o modelo de pH do sangue nesta situação é $latex \text{pH}=6.1+ \log (\frac{800}{x})$, onde x é a pressão parcial de dióxido de carbono nas artérias, medido em torr.
Encontre a pressão parcial do dióxido de carbono nas artérias se o pH for 7,2.
Solução: Usamos $latex \text{pH}=7.2$ na equação logarítmica fornecida e obtemos:
$latex 7.2=6.1+\log \left( \frac{800}{x} \right)$
$latex 1.1=\log \left( \frac{800}{x} \right)$
Resolvendo isso para x, encontramos:
$latex x=\frac{800}{{{10}^{1.1}}}=63.55$
Portanto, a pressão parcial de dióxido de carbono nas artérias é de 63,55 torr.
Entropia de informação
Outra aplicação das funções logarítmicas é com a entropia da informação. A entropia da informação H, em bits, de uma senha gerada aleatoriamente com L caracteres é dada por $latex L \log_{2}(N)$, onde N é o número de símbolos possíveis para cada caractere da senha. Em geral, quanto maior a entropia, mais forte é a senha.
EXEMPLO
- Se uma senha de 8 caracteres diferencia maiúsculas de minúsculas, ou seja, maiúsculas e minúsculas são consideradas caracteres diferentes, ela é composta apenas por letras e números, encontre a entropia da informação.
Solução: Existem 26 letras no alfabeto, 52 se maiúsculas e minúsculas forem contadas separadamente. Existem 10 dígitos de 0 a 9. Isso equivale a um total de $latex N = 61$ símbolos. Como a senha deve ter 8 caracteres, temos $latex L=8$. Portanto:
$latex H=8\log_{2}(61)$
$latex H=\frac{8\ln(61)}{\ln(2)}=47.45$
- Quantos símbolos por caractere precisamos para produzir uma senha de 6 caracteres com entropia de 40 bits?
Solução: Temos $latex L=6$ e $latex H=40$ e temos que encontrar N. Então, temos:
$latex 40=6\log_{2}(N)$
⇒ $latex N={{2}^{\frac{40}{6}}}=101.6$
Portanto, precisaríamos de 102 caracteres para obter uma senha com entropia de 40 bits.
Veja também
Você quer aprender mais sobre aplicações de funções? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
