Os ângulos suplementares são um par de ângulos que, quando adicionados, medem 180 graus. Por exemplo, os ângulos 140° e 40° são complementares, pois somados obtemos 180 graus. Quando unimos dois ângulos suplementares, formamos uma linha reta.
A seguir, veremos uma definição mais detalhada dos ângulos suplementares junto com diagramas para ilustrar os conceitos. Além disso, aprenderemos a encontrar esses ângulos e veremos alguns exercícios onde aplicaremos o que aprendemos.
O que é um ângulo suplementar?
Os ângulos suplementares são pares de ângulos em que a soma de seus ângulos é igual a 180 graus. Esses ângulos sempre vêm em pares, então um ângulo é o complemento de outro ângulo.
Embora a medida de um ângulo em linha reta seja de 180 graus, não é considerado um ângulo suplementar, pois não aparece em pares. Da mesma forma, não podemos ter três ângulos ou mais ângulos suplementares, embora sua soma possa ser igual a 180 graus.
EXEMPLOS
A seguir estão alguns exemplos de ângulos suplementares:
- Dois ângulos, cada um medindo 90 graus.
- Ângulos que medem 50 e 130 graus.
- Ângulos que medem 1 e 179 graus.
Podemos ter vários tipos de ângulos suplementares. Por exemplo, é possível ter ângulos adjacentes, ângulos não adjacentes e ângulos retos.
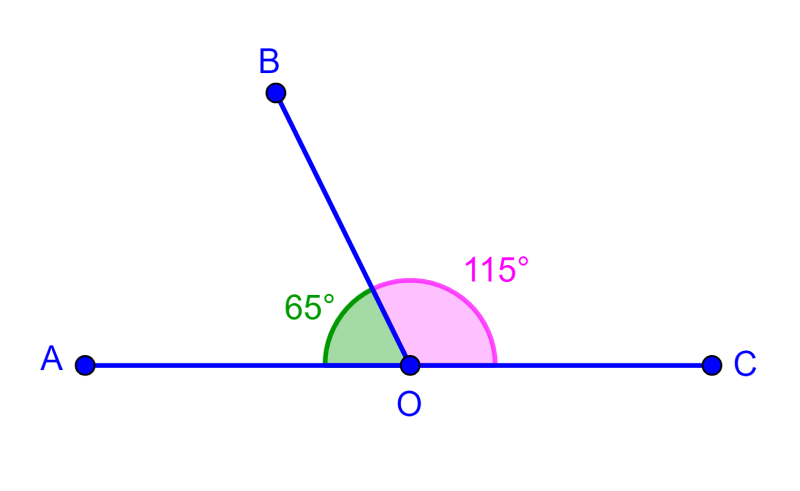
Ângulos suplementares adjacentes
Dois ângulos suplementares com um vértice comum e um segmento comum são chamados de ângulos suplementares adjacentes. Um exemplo desses ângulos é o diagrama a seguir, onde os ângulos compartilham o segmento OB e também somam 180 graus.
Ângulos suplementares não adjacentes
Esses ângulos têm a característica de serem complementares, mas não adjacentes. Isso significa que eles não compartilham um vértice ou um segmento. No exemplo a seguir, podemos ver que os ângulos não têm um vértice comum ou um segmento comum. No entanto, esses ângulos são complementares, pois somam 180° e formam uma linha reta quando unidos.
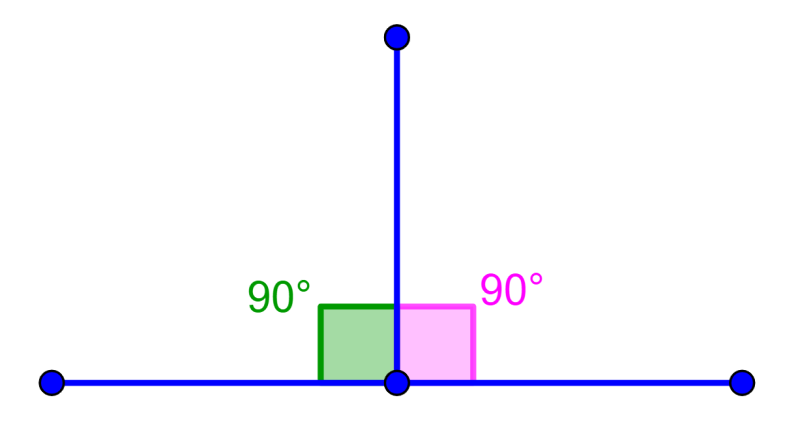
Ângulos suplementares retos
Um ângulo suplementar pode ser formado por dois ângulos retos. Lembre-se de que os ângulos retos têm um ângulo de 90° como no diagrama a seguir.
Como encontrar um ângulo suplementar?
Quando a soma de dois pares de ângulos é igual a 180 graus, chamamos esse par de ângulos de suplementos um ao outro. Portanto, sabemos que a soma de dois ângulos suplementares é de 180 graus e cada um deles é chamado de suplemento do outro. Isso significa que o suplemento de um ângulo é encontrado subtraindo esse ângulo de 180 graus.
Em termos gerais, se tivermos o ângulo x°, seu suplemento é (180-x)°. Por exemplo, o suplemento do ângulo de 75° é obtido subtraindo-o de 180°. Portanto, seu suplemento é (180-75)° = 105°.
Propriedades dos ângulos suplementares
A seguir estão algumas das propriedades fundamentais dos ângulos suplementares:
- Dois ângulos são complementares se somam 180 graus.
- Três ou mais ângulos não podem ser complementares, mesmo se a soma deles for 180 graus.
- Os ângulos suplementares podem ser adjacentes ou não adjacentes.
- Quando unimos dois ângulos suplementares, formamos uma linha reta.
- Se dois ângulos são suplementares, cada ângulo é denominado “suplemento” ou “ângulo suplementar” do outro ângulo.
Exercícios de ângulos suplementares resolvidos
Os conceitos aprendidos sobre ângulos suplementares são aplicados para resolver os exercícios a seguir. Cada exercício tem sua respectiva solução, onde são detalhados o processo e o raciocínio utilizado.
EXERCÍCIO 1
Determine se os ângulos 132° e 48° são ângulos suplementares.
Solução
Sabemos que os ângulos suplementares somam 180°. Portanto, verificamos se os ângulos dados são complementares, adicionando-os:
132° + 48° = 180°
Vemos que obtivemos 180°, portanto os ângulos dados são complementares.
EXERCÍCIO 2
Se tivermos o ângulo de 57°, qual é o seu ângulo suplementar?
Solução
Podemos encontrar o ângulo suplementar subtraindo o ângulo dado de 180°. Então, temos:
180° – 57° = 123°
O ângulo suplementar de 57° é 123°.
EXERCÍCIO 3
Encontre os ângulos suplementares que têm uma diferença de 28°.
Solução
Vamos usar x para representar um dos ângulos. Como são complementares, o outro ângulo será (180-x) °. A diferença entre esses ângulos é 28, então temos:
(180°-x)-x = 28°
180°-2x = 28°
2x = 152°
x = 76°
⇒ 180°-x = 180°-76°
= 104°
Os dois ângulos suplementares são 76° e 104°.
EXERCÍCIO 4
Qual é o ângulo suplementar de $latex \frac{2}{3}$ de 120°?
Solução
Temos que começar calculando o ângulo dado:
$latex 120^{\circ}\times \frac{2}{3} =80^{\circ}$
⇒ $latex 180^{\circ}-80^{\circ}=100^{\circ}$
Portanto, o ângulo suplementar é de 100°.
EXERCÍCIO 5
Encontre o ângulo que é 68° menor que seu suplemento.
Solução
Novamente, vamos usar x para representar o ângulo que queremos encontrar. Isso significa que o ângulo suplementar é $latex (180^{\circ} -x)$. Pela pergunta, sabemos que a diferença entre o ângulo e seu suplemento é de 68°, então temos:
$latex (180-x)-x=68$
$latex 180-2x=68$
$latex -2x=68-180$
$latex -2x=-112$
$latex x=56$
O ângulo é de 56°.
Exercícios de ângulos suplementares para resolver
Coloque em prática o que você aprendeu sobre ângulos suplementares para resolver os exercícios a seguir. Se precisar de ajuda com isso, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre ângulos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
