Ângulos alternos internos são os ângulos formados quando uma transversal cruza duas linhas paralelas ou não paralelas. Esses ângulos estão localizados no interior das linhas paralelas, mas em lados opostos da transversal. A transversal atravessa as duas linhas, que são coplanares, em pontos diferentes. Esses ângulos representam se as duas linhas fornecidas são paralelas entre si ou não. Se esses ângulos forem iguais, então as linhas cruzadas pela transversal são paralelas.
Exploraremos esses ângulos com mais detalhes a seguir. Usaremos diagramas para ilustrar os conceitos e aprenderemos sobre algumas de suas propriedades mais importantes. Além disso, aprenderemos sobre o teorema dos ângulos alternos internos e veremos seu teste.
O que são ângulos alternos internos?
Ângulos alternos internos são ângulos formados quando duas linhas paralelas ou não paralelas são interceptadas por uma transversal. Esses ângulos estão localizados nos cantos internos das interseções e em lados opostos da transversal.
Esses ângulos são iguais se as linhas interceptadas pela transversal forem paralelas. Por outro lado, os ângulos alternos internos formados quando uma transversal cruza duas linhas não paralelas não têm relação geométrica.
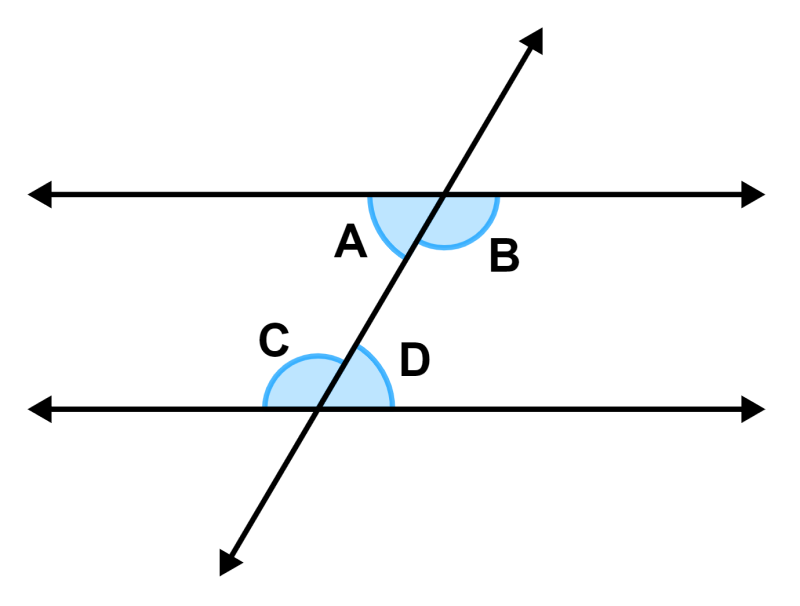
Vamos considerar o seguinte diagrama:
Podemos ver que as duas linhas paralelas são interceptadas por uma transversal. Isso significa que os ângulos alternados dentro das linhas paralelas serão iguais. Ou seja, temos:
∠A = ∠D e ∠B = ∠C
Propriedades de ângulos alternos internos
A seguir estão algumas das propriedades importantes de ângulos alternos internos:
- Se as duas linhas são paralelas, os ângulos são congruentes.
- Os ângulos internos consecutivos são complementares, ou seja, somam 180°.
- No caso de linhas não paralelas, ângulos alterenos internos não têm propriedades específicas.
Teorema dos ângulos alternos internos
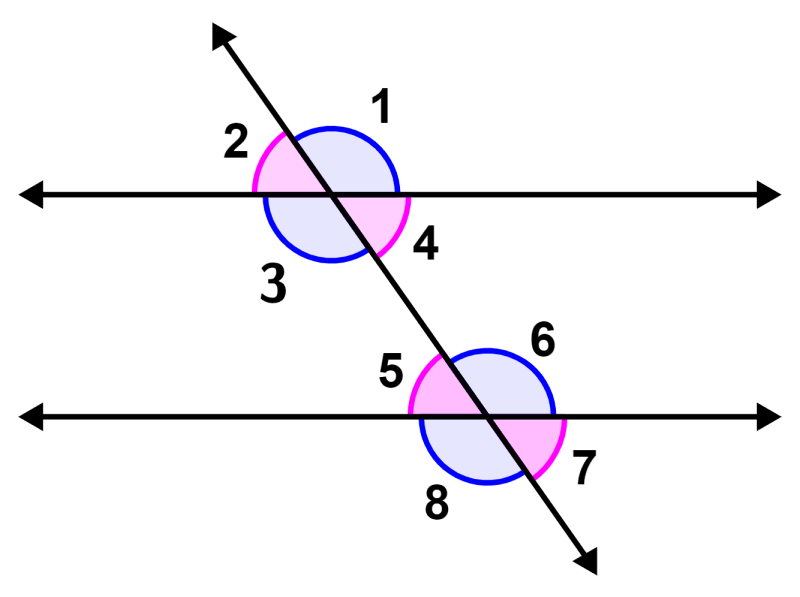
Este teorema indica que, “se uma transversal cruza duas linhas paralelas, os ângulos alternos internos são congruentes.” Para provar este teorema, considere o seguinte diagrama:
Pelas propriedades das linhas paralelas, sabemos que se uma transversal cruza duas linhas paralelas, os ângulos correspondentes e os ângulos verticais opostos são iguais. Então, temos:
∠2 = ∠5 (ângulos correspondentes)
∠2 = ∠4 (ângulos verticais opostos)
A partir dessas duas igualdades, podemos concluir que:
∠4 = ∠5 (ângulos alternos internos)
Da mesma forma, também temos:
∠3 = ∠6 (ângulos alternos internos)
Ângulos co-internos
Os ângulos co-interiores são os ângulos que estão do mesmo lado da transversal. Os ângulos co-internos somam 180°. Isso significa que os ângulos internos, que estão do mesmo lado da transversal, são complementares.
Os ângulos co-internos têm a forma de um “C” e esses ângulos não são iguais entre si. Esses ângulos também são conhecidos como ângulos internos consecutivos ou ângulos internos do mesmo lado.
Exercícios de ângulos alternos internos resolvidos
EXEMPLO 1
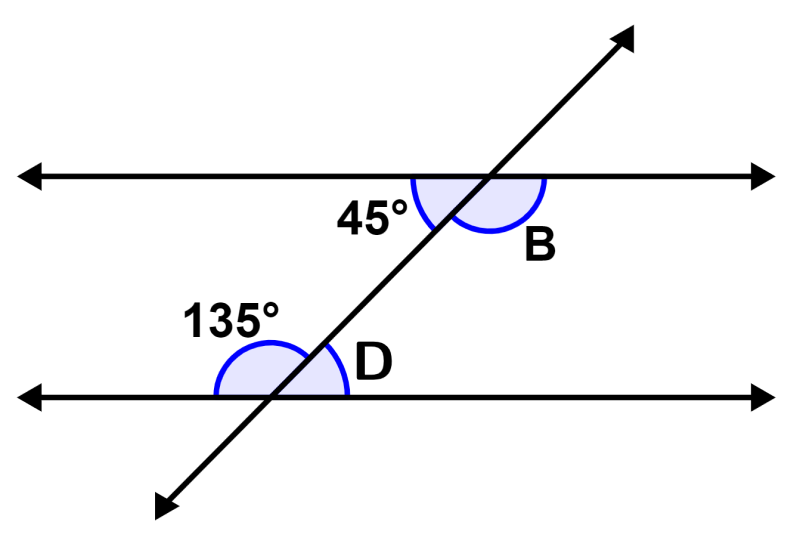
Encontre o valor de B e D na figura a seguir:
Solução: Uma vez que o ângulo de 45° e D são ângulos internos alternados, sabemos que eles são congruentes, então temos:
D = 45°
Da mesma forma, o ângulo de 135° e B são ângulos alternos internos, então temos:
B = 135°
EXEMPLO 2
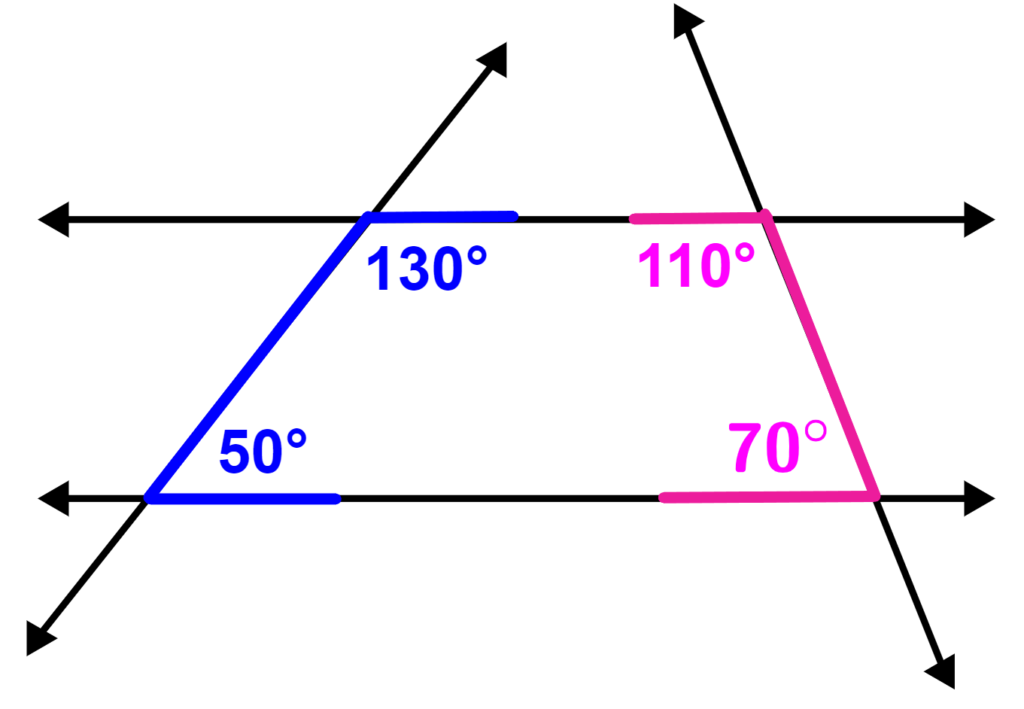
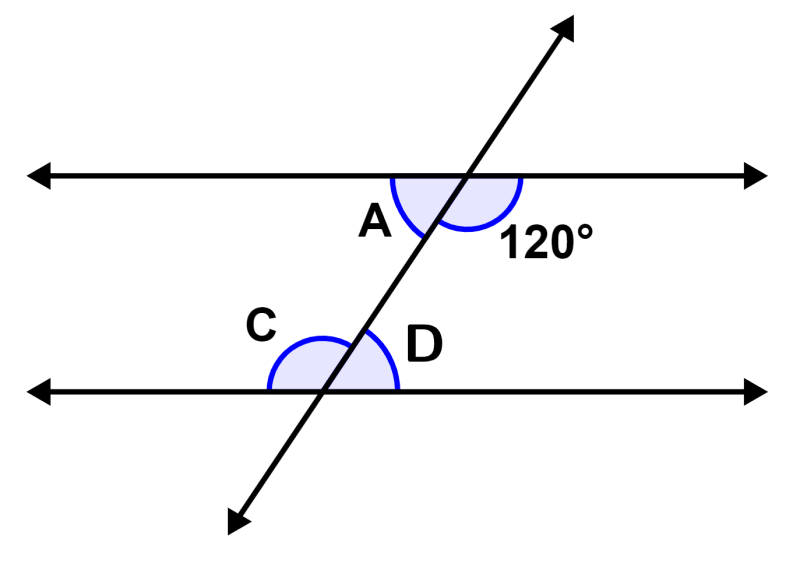
Encontre o valor de A, C e D na figura a seguir:
Solução: Os ângulos ∠A, 120°, ∠C e ∠D são ângulos internos, então sabemos que temos:
∠C = 120°
Pelo teorema dos ângulos suplementares, sabemos que temos:
∠C+∠D = 180°
∠D = 180° – ∠C = 180° – 120° = 60°
EXEMPLO 3
Se tivermos que os ângulos (4x-19)° e (3x + 16)° são ângulos alternos internos congruentes, qual é o valor de x?
Solução: Os ângulos são congruentes, então temos:
4x-19 = 3x+16
4x-3x = 16+19
x = 35
Isso significa que os ângulos fornecidos são iguais a:
4(35)-19 = 121°
EXEMPLO 4
Dois ângulos internos consecutivos são (2x + 10)° e (x + 5)°. Encontre a medida dos ângulos.
Solução: Ângulos internos consecutivos são complementares, então temos:
(2x+10) + (x+5) = 180
3x+15 = 180
3x = 165
x = 55
Portanto, os ângulos internos consecutivos são:
2x+10 = 2(55)+10 = 120°
x+5 = 55+5 = 60°
Veja também
Você quer aprender mais sobre ângulos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
