Os ângulos alternos externos são um par de ângulos formados do lado de fora de duas linhas que são cruzadas por uma terceira linha. Os ângulos alternos estão localizados em lados opostos da linha transversal. Dependendo da natureza das linhas, os ângulos terão algumas características. Por exemplo, se as duas linhas são paralelas, os ângulos alternos externos serão iguais.
Exploraremos esses tipos de ângulos com mais detalhes a seguir. Ilustraremos os conceitos usando diagramas e conheceremos as propriedades fundamentais desses ângulos. Além disso, aprenderemos sobre o teorema dos ângulos alternos externos e veremos alguns exercícios resolvidos.
O que são ângulos alternos externos?
Ângulos externos alternativos são ângulos criados quando três linhas se cruzam. Quando uma linha cruzada cruza as outras duas linhas, ela cria um exterior e um interior para as linhas paralelas. Esses ângulos são criados no espaço fora das linhas paralelas em lados alternados.
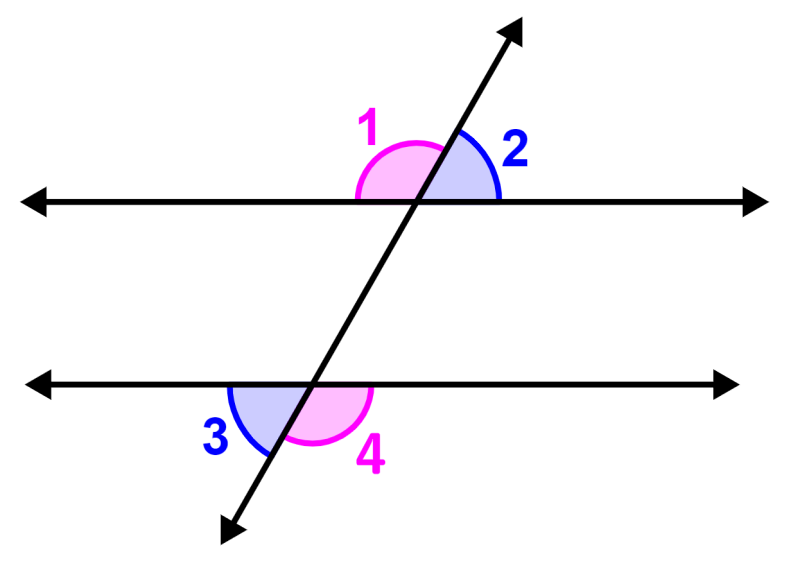
No diagrama a seguir, temos duas linhas paralelas que são cruzadas por uma linha transversal. Podemos listar os vértices externos da seguinte maneira:
Portanto, temos os quatro ângulos externos:
- ∠1
- ∠2
- ∠3
- ∠4
Ângulos alternos externos são pares que aparecem fora das linhas cruzadas e em linhas diferentes. Neste caso, os ângulos alternos externos são:
- ∠1 e ∠4
- ∠2 e ∠3
Propriedades de ângulos alternos externos
A seguir estão as propriedades fundamentais dos ângulos alternos externos:
- Quando as duas linhas são paralelas, os ângulos alternos externos são congruentes (eles têm a mesma medida).
- Os ângulos externos consecutivos são complementares (somam 180°).
- Quando as duas linhas não são paralelas, os ângulos alternos externos não têm propriedades específicas.
Teorema dos ângulos alternos externos
Quando duas linhas são paralelas, a transversal cria ângulos alternos externos. O teorema diz: “Se um par de linhas paralelas é cruzado por uma transversal, então os ângulos alternos externos são congruentes.”
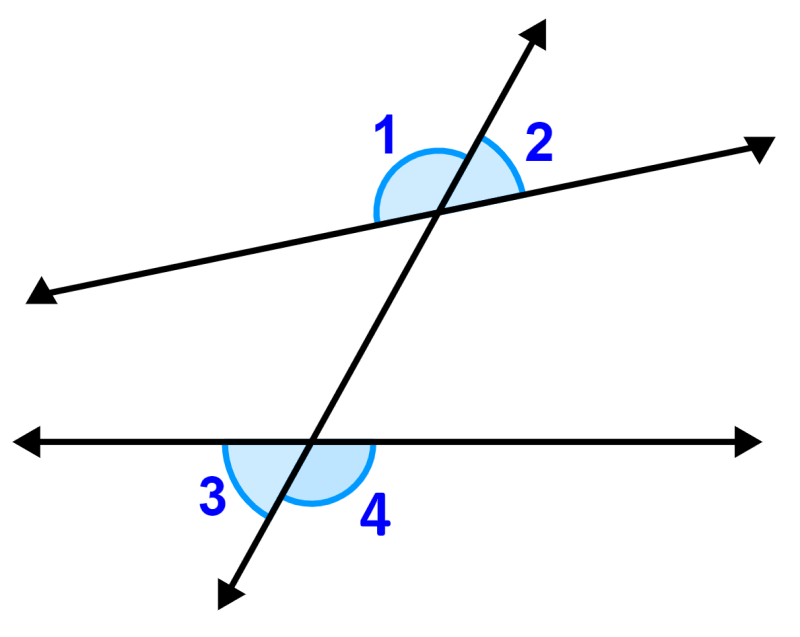
No diagrama a seguir, temos um par de linhas paralelas que são cruzadas por uma transversal.
Temos os mesmos ângulos externos:
- ∠1
- ∠2
- ∠3
- ∠4
Usando o teorema dos ângulos alternos externos, sabemos que os ângulos alternos externos formados por linhas paralelas são congruentes, então temos:
- ∠1 = ∠4
- ∠2 = ∠3
Teorema inverso dos ângulos alternos externos
O oposto do teorema dos ângulos alternos externos também é verdadeiro: “Se os ângulos alternos externos de duas linhas cruzadas por uma transversal são congruentes, então as linhas são paralelas.”
Então, se tivermos que os ângulos ∠1 e ∠4 são iguais, sabemos automaticamente que as linhas devem ser paralelas.
Exercícios de ângulos alternos externos resolvidos
EXEMPLO 1
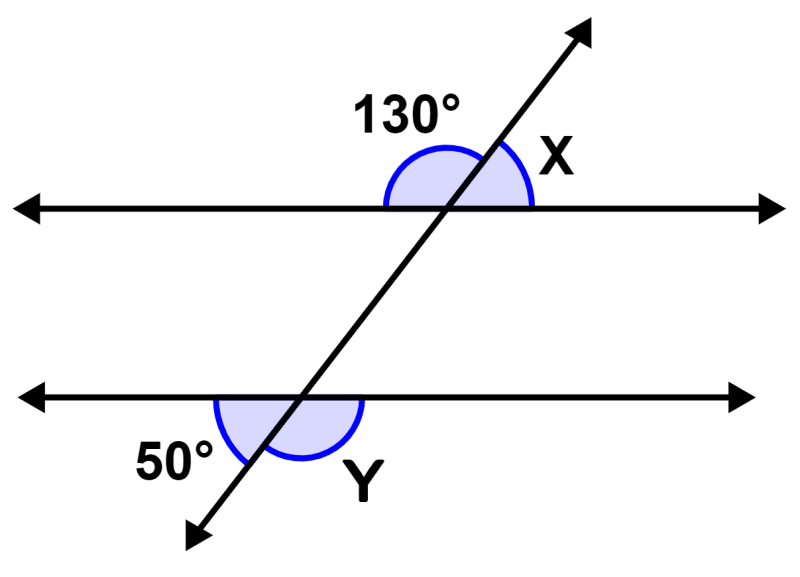
Qual é o valor de X e Y na figura a seguir?
Solução: Os ângulos 50° e Y são ângulos alternos externos. Uma vez que as linhas são paralelas, sabemos que temos :
Y = 50°
Da mesma forma, os ângulos 130° e Y são ângulos externos alternados, então temos:
X = 130°
EXEMPLO 2
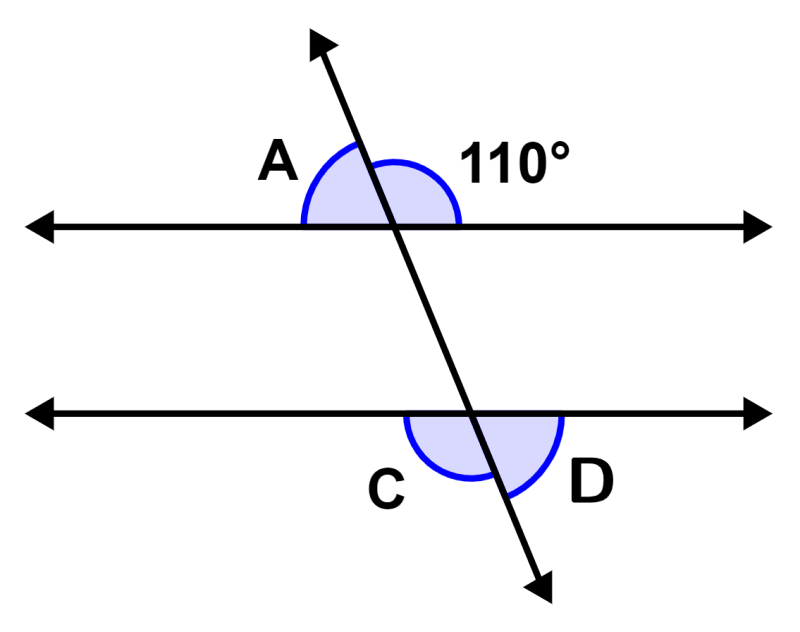
Qual é o valor dos ângulos ausentes no diagrama?
Solução: Os ângulos ∠A, 110°, ∠C e ∠D são ângulos externos. Uma vez que as linhas são paralelas, temos:
∠C = 110°
Além disso, sabemos que ângulos consecutivos são suplementares, então temos:
∠C+∠D = 180°
∠D = 180° – ∠C = 180° – 110° = 70°
EXEMPLO 3
Temos que os ângulos (5x-25)° e (3x+35)° são ângulos alternos externos congruentes. Qual é o valor de x?
Solução: Sabemos que ângulos congruentes têm a mesma medida, então temos:
5x-25 = 3x+35
5x-3x = 25+35
2x = 60
x = 30
Portanto, os ângulos dados são:
5(30)-25 = 125°
EXEMPLO 4
Temos os ângulos exteriores consecutivos (3x-10)° e (x + 30)°. Encontre a medida dos ângulos.
Solução: Sabemos que ângulos externos consecutivos são complementares, então podemos formar a seguinte equação:
(3x-10) + (x+30) = 180
4x+20 = 180
4x = 160
x = 40
Então, os ângulos são:
3x-10 = 3(40)-10 = 110°
x+30 = 40+30 = 70°
Veja também
Você quer aprender mais sobre ângulos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
