Os pontos máximos, mínimos e de inflexão são chamados de pontos estacionários de uma função. As coordenadas desses pontos podem ser encontradas usando a derivada da função. O declive nos pontos máximo, mínimo e de inflexão é igual a zero. Então, temos que encontrar as raízes da derivada.
A seguir, aprenderemos sobre pontos de máximo, mínimo e inflexão de funções. Além disso, conheceremos como encontrar as coordenadas desses pontos com exemplos.
- Definição do ponto máximo de uma função
- Encontrar as coordenadas do ponto de máximo de uma função
- Definição do ponto mínimo de uma função
- Encontrar as coordenadas do ponto mínimo de uma função
- Definindo os pontos de inflexão de uma função
- Encontrar as coordenadas dos pontos de inflexão de uma função
- Veja também
Definição do ponto máximo de uma função
Os pontos máximos são pontos em que os valores de y da função são os mais altos possíveis que a função pode alcançar. Ou seja, não há nenhum outro ponto na função que tenha um valor maior de y.
O ponto de máximo de uma função é um dos pontos estacionários da função. Nesses pontos, o declive da reta tangente é igual a zero. Isso significa que temos $latex \frac{dy}{dx}=0$.
Podemos usar o seguinte diagrama para ter uma representação gráfica de um ponto de máximo de uma função:

À esquerda de um ponto de máximo, o declive é positivo e à direita do ponto de máximo, o declive é negativo. Ou seja, a função aumenta até atingir o ponto de máximo e depois diminui. Então temos:
- No lado esquerdo de P: $latex \frac{dy}{dx}>0$
- No ponto P: $latex \frac{dy}{dx}=0$
- Do lado direito de P: $latex \frac{dy}{dx}<0$
Como o declive (o valor da derivada) vai de positiva para negativa perto do ponto de máximo, a segunda derivada da função em um ponto de máximo é negativa (a primeira derivada diminui).
Encontrar as coordenadas do ponto de máximo de uma função
Podemos encontrar as coordenadas de um ponto de máximo usando a derivada da função. Para isso, consideramos que o declive em um ponto de máximo é igual a zero.
Então, formamos uma equação com a derivada e encontramos suas raízes (os valores de x). Em seguida, usamos a segunda derivada para identificar qual desses valores é o ponto máximo.
Se conhecermos a função, podemos encontrar seu ponto máximo com os seguintes passos:
Passo 1: Calcule a derivada da função.
Passo 2: Encontre os pontos estacionários com a derivada. Para fazer isso, formamos uma equação com a derivada e resolvemos para x. Ou seja, temos $latex \frac{dy}{dx}=0$.
Passo 3: Determine qual dos pontos do passo 2 é o ponto máximo. Para isso, usamos a segunda derivada.
Quando temos um ponto máximo, devemos ter $latex \frac{d^2y}{dx^2}<0$. Ou seja, a segunda derivada nesse ponto deve ser negativa.
Passo 4: Determine a coordenada y do ponto máximo usando a coordenada x do passo 3.
EXEMPLO
Encontre as coordenadas do ponto máximo de $latex f(x)=\frac{1}{3}x^3+x^2-3x$.
Solução
Passo 1: Começamos encontrando a derivada da função:
$latex f(x)=\frac{1}{3}x^3+x^2-3x$
$latex f'(x)=x^2+2x-3$
Passo 2: Agora, usamos a derivada para encontrar os pontos estacionários:
$latex x^2+2x-3=0$
$latex (x+3)(x-1)=0$
$latex x=-3~~$ ou $latex ~~x=1$
Passo 3: Determinamos qual é o ponto máximo usando a segunda derivada:
$latex f^{\prime \prime}(x)=2x+2$
Quando $latex x=-3$, temos $latex f^{\prime \prime}(x)<0$ e quando $latex x=1$, temos $latex f^{\prime \prime}(x )> 0$. Portanto, o ponto máximo está em $latex x=-3$.
Passo 4: A coordenada y do ponto máximo é:
$latex f(x)=\frac{1}{3}x^3+x^2-3x$
$latex f(x)=\frac{1}{3}(-3)^3+(-3)^2-3(-3)$
$latex y=9$
O ponto máximo tem as coordenadas (-3, 9).
Definição do ponto mínimo de uma função
Os pontos mínimos das funções são os pontos onde os valores de y da função são os mínimos possíveis. Isso significa que não há nenhum outro ponto na função que tenha um valor de y menor que o ponto mínimo.
Pontos mínimos são pontos estacionários de uma função. Nesses pontos, o declive da reta tangente é igual a zero. Ou seja, em um ponto mínimo temos $latex \frac{dy}{dx}=0$.
O diagrama a seguir é uma representação gráfica de um ponto mínimo em uma função:

À esquerda de um ponto mínimo, o declive é negativo e à direita do ponto mínimo, o declive é positivo. Ou seja, a função diminui até atingir o ponto mínimo e depois aumenta. Então temos:
- Do lado esquerdo de P: $latex \frac{dy}{dx}<0$
- No ponto P: $latex \frac{dy}{dx}=0$
- Do lado direito de P: $latex \frac{dy}{dx}>0$
Como o declive (o valor da derivada) vai de negativa a positiva perto do ponto máximo, a segunda derivada da função em um ponto mínimo é positiva (a primeira derivada aumenta).
Encontrar as coordenadas do ponto mínimo de uma função
As coordenadas de um ponto mínimo de uma função são encontradas usando a derivada da função. Lembramos que nesses pontos o declive é igual a zero.
Então, formamos uma equação com a derivada e encontramos suas raízes. Em seguida, usamos a segunda derivada para identificar os pontos mínimos.
Se conhecermos a função, podemos seguir estes passos para determinar seu ponto mínimo:
Passo 1: Obtenha a derivada da função.
Passo 2: Encontre os pontos estacionários usando a derivada. Então, formamos a equação $latex \frac{dy}{dx}=0$ e encontramos os valores de x.
Passo 3: Use a segunda derivada para identificar o ponto mínimo. Para que um ponto estacionário seja mínimo, devemos ter $latex \frac{d^2y}{dx^2}>0$.
Passo 4: Use a coordenada x do passo 3 para encontrar a coordenada y do ponto mínimo.
EXEMPLO
Quais são as coordenadas do ponto mínimo da função $latex f(x)=2x^3-6x$?
Solução
Passo 1: Começamos encontrando a derivada da função:
$latex f(x)=2x^3-6x$
$latex f'(x)=6x^2-6$
Passo 2: Determinamos os valores de x a partir da equação formada pela derivada:
$latex 6x^2-6=0$
$latex x=\sqrt{1}$
$latex x=\pm 1$
$latex x=1~~$ ou $latex ~~x=-1$
Passo 3: Usamos a segunda derivada para determinar a natureza dos pontos estacionários encontrados:
$latex f^{\prime \prime}(x)=12x$
Quando $latex x=1$, temos $latex f^{\prime \prime}(x)>0$ e quando $latex x=-1$, temos $latex f^{\prime \prime}(x ) < 0$. Isso significa que $latex x=1$ é o ponto mínimo.
Passo 4: A coordenada y do ponto mínimo é:
$latex y=2x^3-6x$
$latex y=2(1)^3-6(1)$
$latex y=-4$
O ponto mínimo da função é (1, -4).
Definindo os pontos de inflexão de uma função
Os pontos de inflexão de uma função são pontos estacionários onde o declive é igual a zero. Ou seja, em um ponto de inflexão temos $latex \frac{dy}{dx}=0$.
A diferença entre os pontos de inflexão e os pontos de mínimo ou máximo é que nos pontos de inflexão, o declive tem o mesmo sinal em ambos os lados do ponto.
No diagrama a seguir, podemos ver uma representação gráfica de ambos os casos dos pontos de inflexão de uma função:
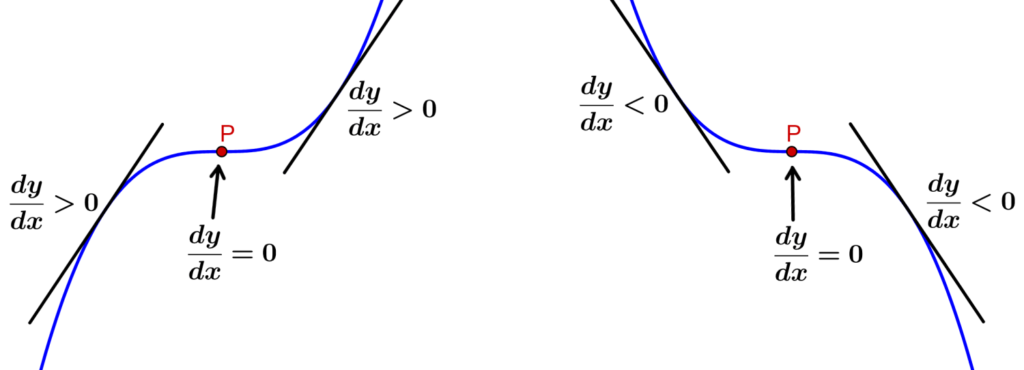
No ponto de inflexão esquerdo, a função cresce em ambos os lados do ponto de inflexão. Ou seja, o declive é positivo em ambos os lados, então temos o seguinte:
- Do lado esquerdo de P: $latex \frac{dy}{dx}>0$
- No ponto P: $latex \frac{dy}{dx}=0$
- Do lado direito de P: $latex \frac{dy}{dx}>0$
No ponto de inflexão à direita, a função diminui em ambos os lados do ponto de inflexão. Ou seja, o declive é negativa em ambos os lados, então temos o seguinte:
- Do lado esquerdo de P: $latex \frac{dy}{dx}<0$
- No ponto P: $latex \frac{dy}{dx}=0$
- Do lado direito de P: $latex \frac{dy}{dx}<0$
Encontrar as coordenadas dos pontos de inflexão de uma função
As coordenadas dos pontos de inflexão podem ser encontradas usando a derivada da função. Para isso consideramos que o declive nos pontos de inflexão é igual a zero.
Então, formamos uma equação com a derivada da função e encontramos os valores de x. Em seguida, usamos a segunda derivada para determinar qual dos pontos é um ponto de inflexão.
Se conhecemos a função, podemos seguir estes passos para determinar as coordenadas dos pontos de inflexão:
Passo 1: Calcule a derivada da função.
Passo 2: Use a derivada para encontrar os pontos estacionários da função. Para isso, formamos a equação $latex \frac{dy}{dx}=0$ e determinamos os valores de x.
Passo 3: Use a segunda derivada para identificar pontos de inflexão. Quando temos um ponto de inflexão, devemos ter $latex \frac{d^2y}{dx^2}=0$.
No entanto, os pontos máximos ou pontos mínimos também podem ter uma segunda derivada igual a zero. Por esta razão, devemos verificar os sinais de cada lado dos pontos de inflexão.
Para que um ponto estacionário seja um ponto de inflexão, o declive deve ter o mesmo sinal em ambos os lados do ponto. Ou seja, a derivada deve ter o mesmo sinal.
Passo 4: Use as coordenadas x do passo 3 para encontrar as coordenadas y dos pontos de inflexão.
EXEMPLO
Encontre as coordenadas do ponto de inflexão da função $latex f(x)=x^3-9x^2+27x-29$.
Solução
Passo 1: Segue a derivada da função:
$latex f(x)=x^3-9x^2+27x-29$
$latex f'(x)=3x^2-18x+27$
Passo 2: Usando a derivada, encontramos os pontos estacionários:
$latex 3x^2-18x+27=0$
$latex 3(x^2-6x+9)=0$
$latex 3(x-3)(x-3)=0$
$latex x=3$
Passo 3: Usamos a segunda derivada para determinar se o ponto é um ponto de inflexão:
$latex f^{\prime \prime}(x)=6x-18$
Quando $latex x=3$, temos $latex f^{\prime \prime}(x)=0$.
Além disso, quando usamos $latex x=3,1$ (direita do ponto) e $late x=2,9$ (esquerda do ponto) na primeira derivada, obtemos dois valores positivos, confirmando assim que é um ponto de inflexão.
Passo 4: A coordenada y do ponto de inflexão é:
$latex y=x^3-9x^2+27x-29$
$latex y=(3)^3-9(3)^2+27(3)-29$
$latex y=-2$
As coordenadas do ponto de inflexão são (3, -2).
Veja também
Interessado em aprender mais sobre derivadas e pontos estacionários? Você pode olhar para estas páginas:




