As coordenadas dos pontos de inflexão de uma função são encontradas usando a derivada da função. Depois, encontramos as raízes da derivada e analisamos a natureza desses pontos. Nos pontos de inflexão, o declive tem o mesmo sinal em ambos os lados do ponto.
A seguir, aprenderemos sobre pontos de inflexão de funções. Vamos saber como encontrar esses pontos e resolver alguns exercícios práticos.
Quais são os pontos de inflexão de uma função?
Os pontos de inflexão de uma função são pontos estacionários que têm como principal característica o declive ter o mesmo sinal em ambos os lados do ponto.
Os pontos estacionários das funções são os pontos onde o declive é igual a zero. Isso significa que nos pontos de inflexão temos $latex \frac{dy}{dx}=0$.
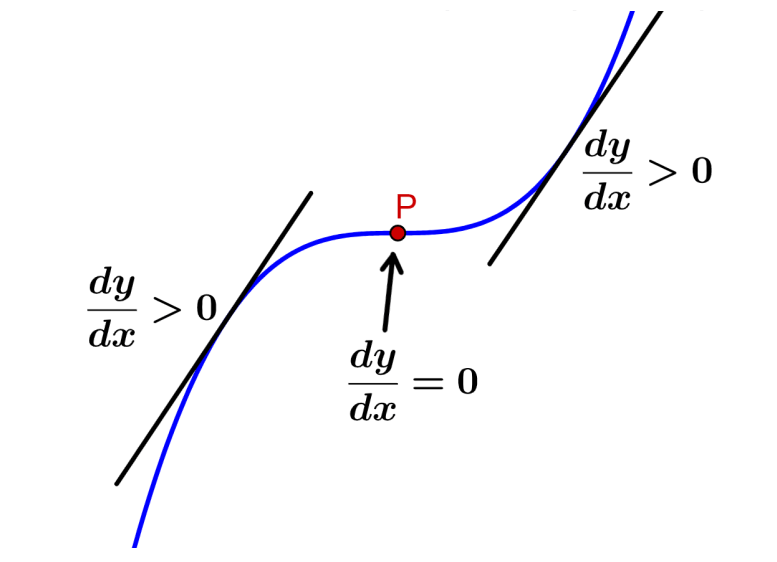
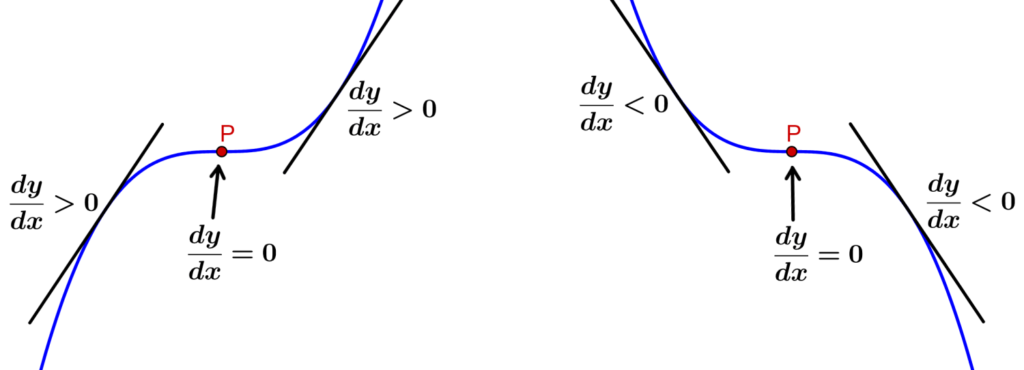
No diagrama a seguir, podemos observar os dois casos de pontos de virada:
No ponto de inflexão à esquerda, o declive é positivo em ambos os lados do ponto de inflexão. Ou seja, a função cresce da esquerda para a direita, então temos o seguinte:
- No lado esquerdo de P: $latex \frac{dy}{dx}>0$
- No ponto P: $latex \frac{dy}{dx}=0$
- Do lado direito de P: $latex \frac{dy}{dx}>0$
No ponto de inflexão à direita, o declive é negativo em ambos os lados do ponto de inflexão. Ou seja, a função diminui da esquerda para a direita, então temos o seguinte:
- Do lado esquerdo de P: $latex \frac{dy}{dx}<0$
- No ponto P: $latex \frac{dy}{dx}=0$
- Do lado direito de P: $latex \frac{dy}{dx}<0$
Como encontrar os pontos de inflexão de uma função?
Para encontrar os pontos de inflexão, usamos a derivada da função para encontrar os pontos estacionários. Depois, podemos diferenciar os pontos de inflexão com a segunda derivada ou com os sinais da derivada em cada lado do ponto.
Lembre-se de que os pontos estacionários são caracterizados pelo fato de o declive nesses pontos ser igual a zero. Então, usamos a derivada da função para formar uma equação e encontrar suas raízes.
Seguimos os seguintes passos para encontrar os pontos de inflexão de uma função:
Passo 1: Obtenha a derivada da função.
Passo 2: Encontre os pontos estacionários usando a derivada. Para isso, formamos a equação $latex \frac{dy}{dx}=0$ e encontramos os valores de x.
Passo 3: Determine quais dos pontos estacionários são pontos de inflexão. Quando temos um ponto de inflexão, devemos ter $latex \frac{d^2y}{dx^2}=0$.
No entanto, a segunda derivada também pode ser zero em um ponto máximo ou mínimo. Portanto, a melhor maneira de identificar pontos de virada é examinar o sinal da derivada em cada lado do ponto.
Para que um ponto estacionário seja um ponto de inflexão, o declive deve ter o mesmo sinal em ambos os lados do ponto.
Passo 4: Use as coordenadas x dos pontos de inflexão para encontrar as coordenadas y dos pontos.
Exercícios resolvidos dos pontos de inflexão de uma função
EXERCÍCIO 1
Encontre o ponto de inflexão da função $latex f(x)=x^3+2$.
Solução
Passo 1: A derivada da função é:
$latex f(x)=x^3+2$
$latex f'(x)=3x^2$
Passo 2: Usando a derivada, formamos uma equação e encontramos os valores de x:
$latex 3x^2=0$
$latex x=0$
Passo 3: Usamos a segunda derivada para verificar que o ponto é um ponto de inflexão:
$latex f^{\prime \prime}(x)=6x$
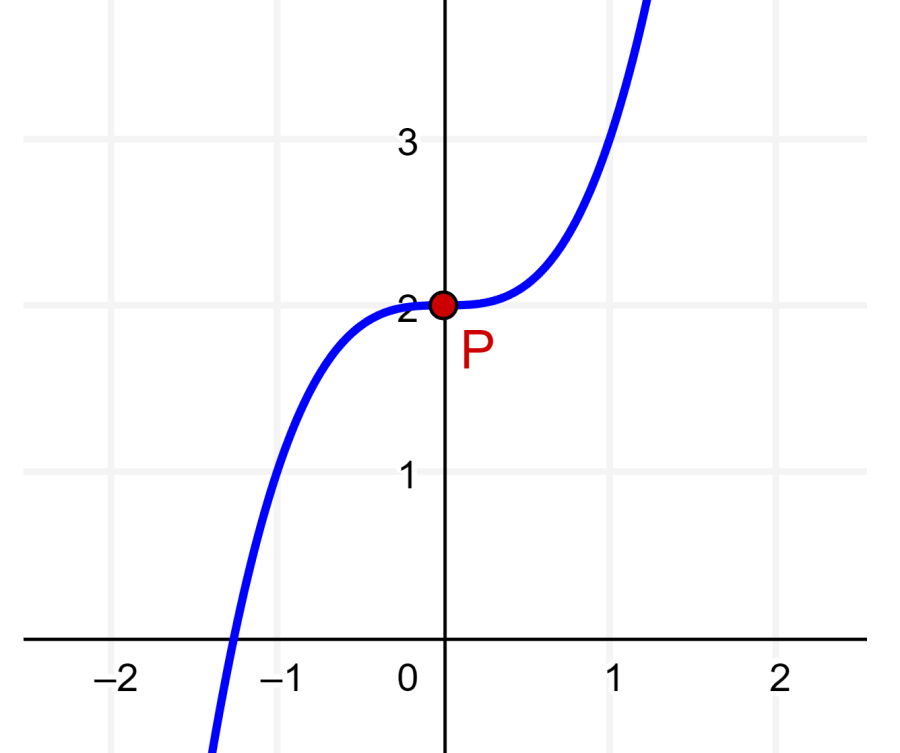
Quando $latex x=0$, temos $latex f^{\prime \prime}(x)=0$. Então, o ponto é um ponto de virada. Podemos usar seu gráfico para verificar completamente:
Passo 4: Usando $latex x=0$ na função, encontramos a coordenada y do ponto:
$latex y=x^3+2$
$latex y=(0)^3+2$
$latex y=2$
As coordenadas do ponto de inflexão são (0, 2).
EXERCÍCIO 2
Quais são as coordenadas do ponto de inflexão da função $latex f(x)=x^5-4$?
Solução
Passo 1: Começamos encontrando a derivada da função:
$latex f(x)=x^5-4$
$latex f'(x)=5x^4$
Passo 2: Encontramos os valores de x na equação formada pela derivada:
$latex 5x^4=0$
$latex x=0$
Passo 3: Verificamos se o ponto é um ponto de inflexão usando a segunda derivada:
$latex f^{\prime \prime}(x)=20x^3$
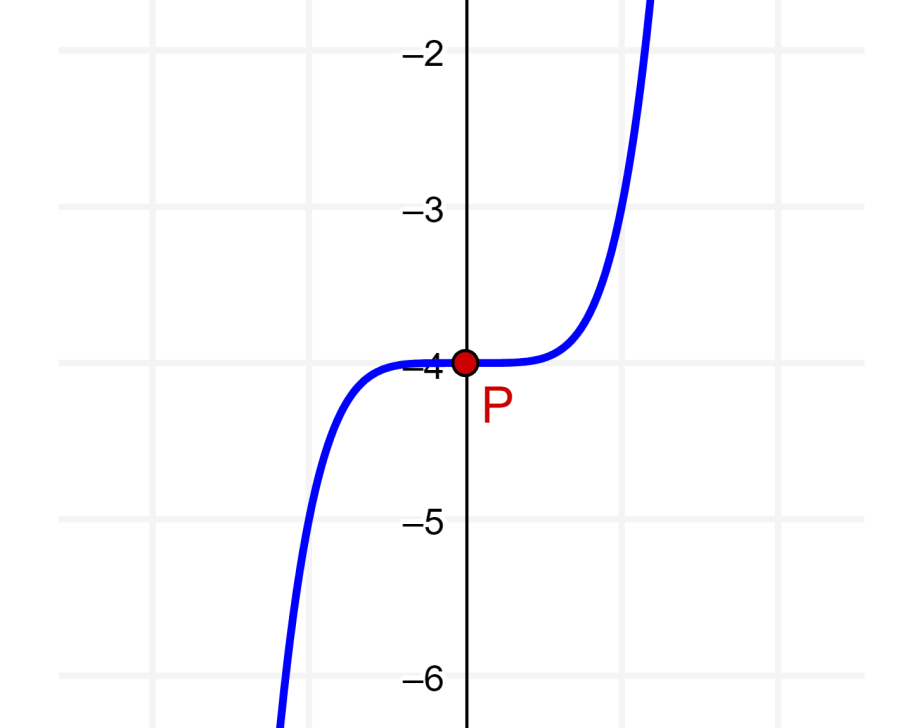
Quando $latex x=0$, temos $latex f^{\prime \prime}(x)=0$. Então, o ponto é um ponto de virada. Podemos usar seu gráfico para verificar completamente:
Passo 4: Encontramos a coordenada y do ponto usando $latex x=0$ na função:
$latex y=x^5-4$
$latex y=(0)^5-4$
$latex y=-4$
As coordenadas do ponto de inflexão são (0, -4).
EXERCÍCIO 3
Encontre o ponto de inflexão da função $latex f(x)=x^3-9x^2+27x-29$.
Solução
Passo 1: Começamos encontrando a derivada da função:
$latex f(x)=x^3-9x^2+27x-29$
$latex f'(x)=3x^2-18x+27$
Passo 2: Formamos uma equação com a derivada para encontrar os valores de x dos pontos estacionários:
$latex 3x^2-18x+27=0$
$latex 3(x^2-6x+9)=0$
$latex 3(x-3)(x-3)=0$
$latex x=3$
Passo 3: Verifique se o ponto é um ponto de inflexão com a segunda derivada:
$latex f^{\prime \prime}(x)=6x-18$
Quando $latex x=3$, temos $latex f^{\prime \prime}(x)=0$.
Além disso, quando usamos $latex x=3,1$ (direita do ponto) e $latex x=2,9$ (esquerda do ponto) na primeira derivada, obtemos dois valores positivos, confirmando assim que é um ponto de inflexão.
Passo 4: Usando $latex x=3$ na função, encontramos a coordenada y do ponto:
$latex y=x^3-9x^2+27x-29$
$latex y=(3)^3-9(3)^2+27(3)-29$
$latex y=-2$
As coordenadas do ponto de inflexão são (3, -2).
EXERCÍCIO 4
Encontre as coordenadas do ponto de inflexão da função $latex f(x)=x^4+4x^3+1$.
Solução
Passo 1: Derivando a função, temos:
$latex f(x)=x^4+4x^3+1$
$latex f'(x)=4x^3+12x^2$
Passo 2: Os valores de x dos pontos estacionários são:
$latex 4x^3+12x^2=0$
$latex 4x^2(x+3)=0$
$latex x=0~~$ ou $latex ~~x=-3$
Passo 3: Usamos a segunda derivada para determinar qual ponto é um ponto de inflexão:
$latex f^{\prime \prime}(x)=12x^2+24x$
Quando $latex x=0$, temos $latex f^{\prime \prime}(x)=0$ e quando $latex x=-3$, temos $latex f^{\prime \prime}(x )> 0$. Então o ponto $latex x=0$ pode ser um ponto de virada.
Usando os valores $latex x=0,1$ e $latex x=-0,1$ na primeira derivada, obtemos declives com o mesmo sinal, então o ponto é de fato um ponto de inflexão.
Passo 4: Usando $latex x=0$ na função, encontramos a coordenada y do ponto:
$latex y=x^4+4x^3+1$
$latex y=(0)^4+4(0)^3+1$
$latex y=1$
As coordenadas do ponto de inflexão são (0, 1).
EXERCÍCIO 5
Quais são os pontos de inflexão da função $latex f(x)=x^4 – 4x^2 + 4$?
Solução
A derivada e a segunda derivada da função são:
$latex f(x)=x^4 – 4x^2 + 4$
$latex f^{\prime}(x)=4x^3-8x$
$latex f^{\prime \prime}(x)=12x^2-8$
Agora, utilizamos a segunda derivada para formar uma equação e encontrar os valores x:
$latex f^{\prime \prime}(x)=12x^2-8=0$
$$x^2=\frac{2}{3}$$
$$x=\pm \sqrt{\frac{2}{3}}$$
Assim, os pontos de inflexão ocorrem nos pontos $latex x=\pm \sqrt{\frac{2}{3}}$.
Agora, usamos esses valores de x para encontrar as coordenadas y:
$$y_{1}=\left(\sqrt{\frac{2}{3}}\right)^4 – 4\left(\sqrt{\frac{2}{3}}\right)^2 + 4$$
$$y_{1}=\frac{4}{3}$$
$$y_{2}=\left(-\sqrt{\frac{2}{3}}\right)^4 – 4\left(-\sqrt{\frac{2}{3}}\right)^2 + 4$$
$$y_{2}=\frac{4}{3}$$
As coordenadas dos pontos de inflexão são $latex \left(\sqrt{\frac{2}{3}}, \frac{4}{3}\right)$ e $latex \left(-\sqrt{\frac{2}{3}}, \frac{4}{3}\right)$.
Pontos de inflexão de uma função – Exercícios para resolver
Quais são as coordenadas do ponto de inflexão na função $latex f(x)=x^3-3x^2+x$?
Escreva as coordenadas na caixa.
Veja também
Interessado em aprender mais sobre derivadas e pontos estacionários? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
