Gráficos de funções podem ser usados para determinar o domínio e a imagem. Os gráficos nos dão uma ideia de quais valores de x e quais valores de y estão sendo tomados. Muitas vezes, isso pode ser suficiente para determinar totalmente o domínio e a imagem. No entanto, haverá momentos em que teremos que usar álgebra para verificar ou ser mais específicos.
A seguir, aprenderemos como determinar o domínio e a imagem de um gráfico de uma função. Veremos vários exemplos para ilustrar essas idéias.
Como encontrar o domínio e a imagem?
Domínio
Lembramos que o domínio de uma função é o conjunto de todos os valores possíveis da variável independente. Ou seja, o domínio é o conjunto de todos os valores de x que resultarão em valores reais de y.
Para encontrar o domínio, devemos lembrar que:
- O denominador de uma fração não pode ser igual a zero.
- O número sob uma raiz quadrada não pode ser um número negativo.
Determinamos o domínio encontrando todos os valores da variável independente que podemos usar e excluindo os valores que não resultam em saídas reais da função.
Imagem
Lembramos que a imagem de uma função é o conjunto de todos os valores possíveis da variável dependente. Ou seja, a imagem é o conjunto de todos os valores de y resultantes ao usar o domínio como entrada.
A imagem pode ser determinada encontrando os valores máximos ou mínimos de y. Além disso, podemos substituir diferentes valores de x e analisar que tipo de valores de y obtemos. Os gráficos são particularmente úteis para determinar a imagem.
Exemplos de domínio e imagem de um gráfico
EXEMPLO 1
Encontre o domínio e a imagem da função f que possui o seguinte gráfico:
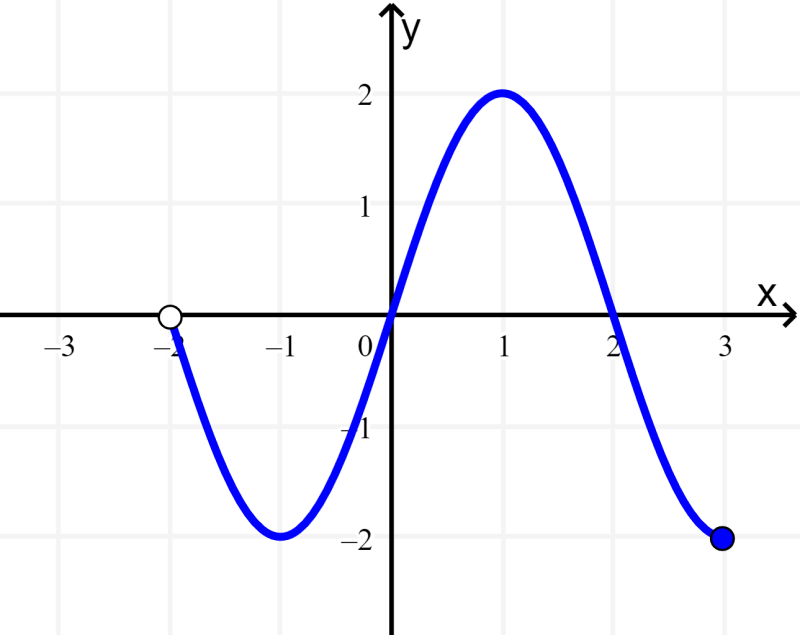
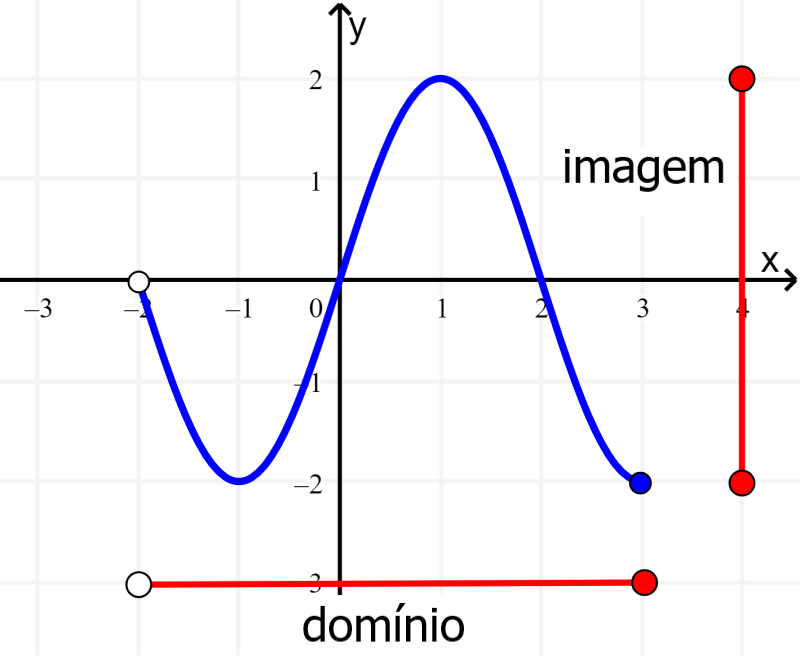
Solução: Podemos ver que o gráfico se estende horizontalmente de -2 a 3, mas o -2 não está incluído. Portanto, o domínio é (-2, 3].
Além disso, vemos que o gráfico se estende verticalmente de 2 a -2, portanto, a imagem é [-2, 2].
EXEMPLO 2
O gráfico a seguir representa a função $latex f(x)=\frac{1}{x+5}$. Determine sua imagem e domínio.
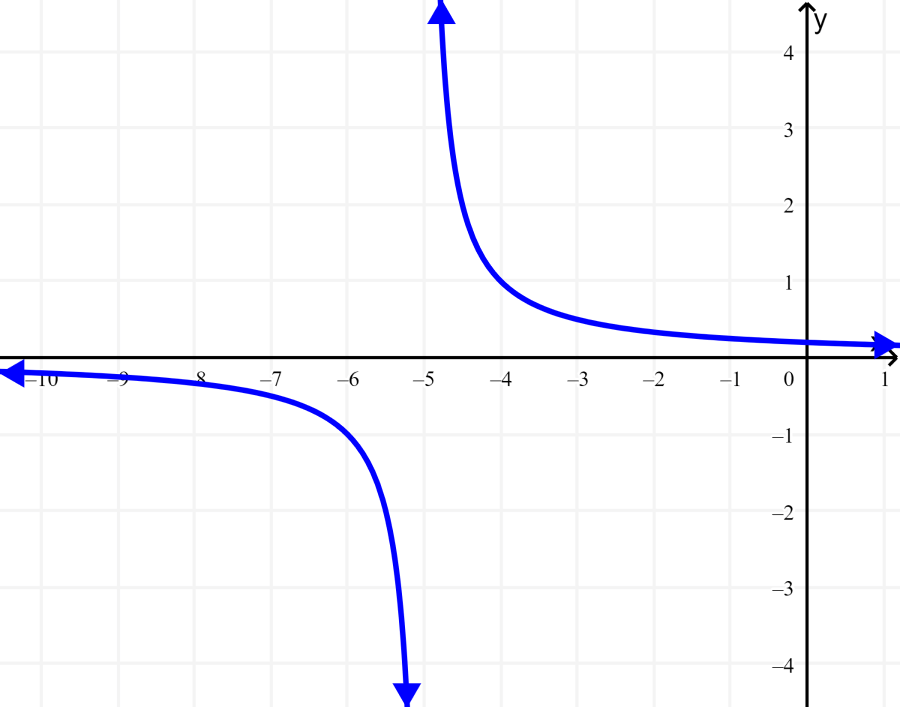
Solução: Podemos ver que o gráfico se estende horizontalmente além do que podemos ver no gráfico, portanto, podemos assumir que se estende do infinito negativo ao infinito positivo.
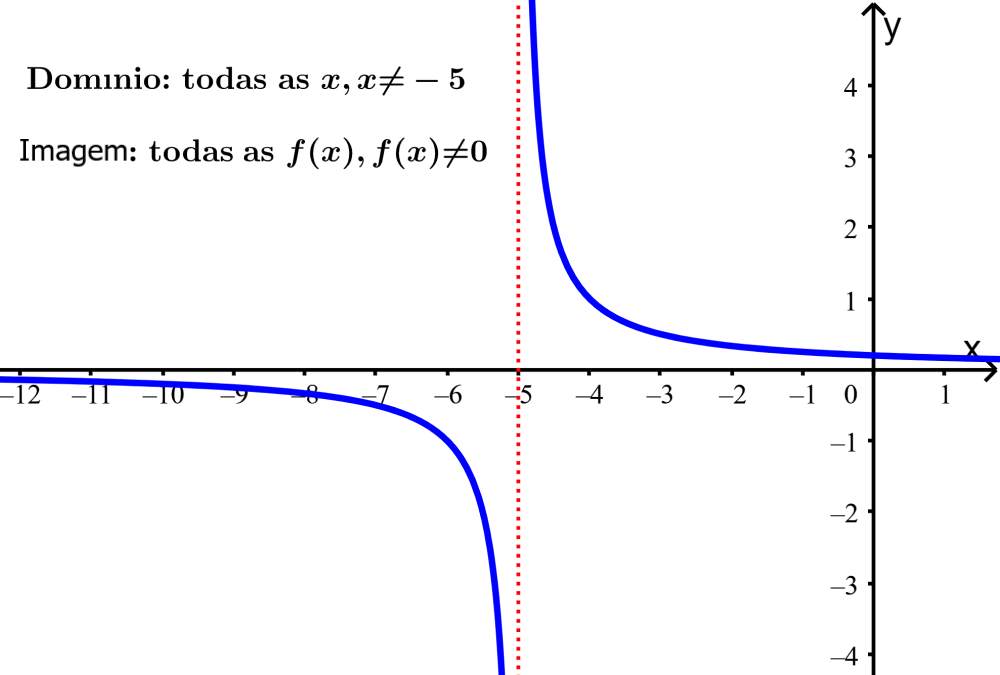
No entanto, podemos ver que o gráfico nunca tem um valor de -5 em x, portanto, temos que excluir esse valor do domínio. Portanto, o domínio são todos os números reais de x e $latex x \neq -5$.
Da mesma forma, vemos que o gráfico se estende verticalmente além do que podemos ver no gráfico, então dizemos que ele se estende do infinito negativo ao infinito positivo. Aqui, vemos que os valores de y nunca chegam a zero, portanto, os excluímos da imagem.
Portanto, a imagem é composto por todos os valores reais de $latex f(x)$ e $latex f(x \neq 0)$.
EXEMPLO 3
O gráfico a seguir representa a função $latex f(x)={{x}^2}+5$. Determine sua imagem e domínio.
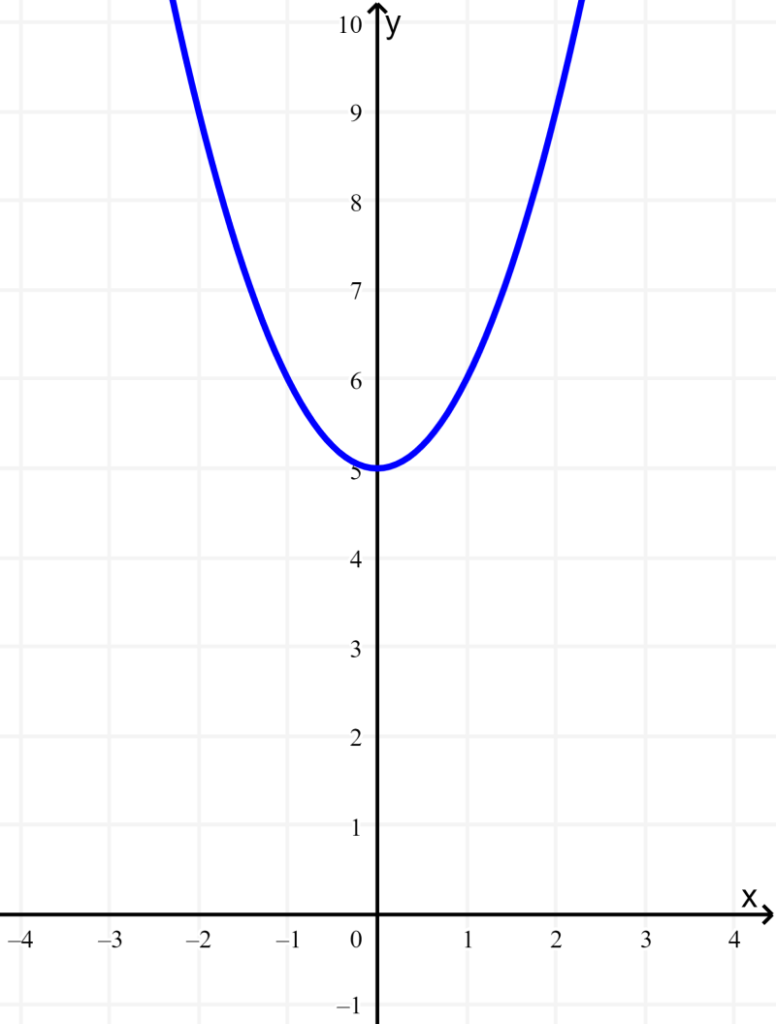
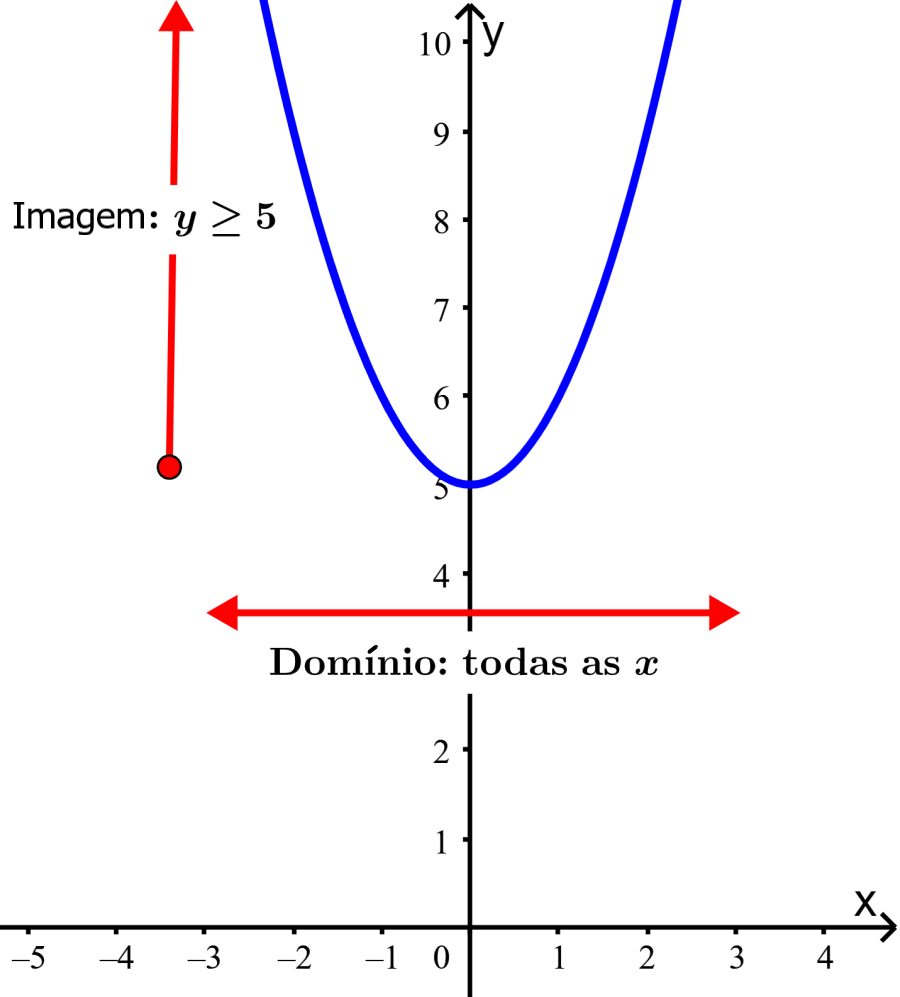
Solução: Este é um gráfico quadrático, portanto, se estende horizontalmente do infinito negativo ao infinito positivo. Isso significa que o domínio é composto de todos os números reais em x.
Também vemos que o gráfico se estende verticalmente de 5 ao infinito positivo. Portanto, a imagem é composto por todos os números reais de y e $latex y ≥ 5$.
EXEMPLO 4
A seguir está o gráfico da função $latex \sqrt{-t+2}$. Qual é o seu domínio e sua imagem?
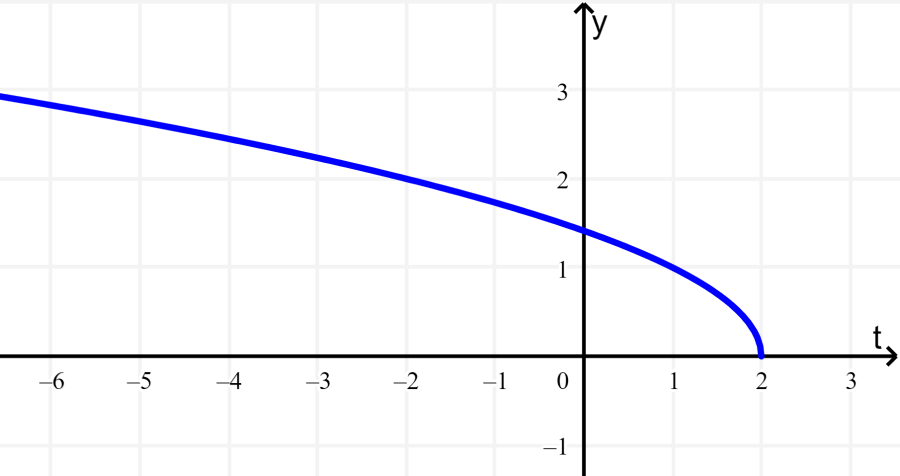
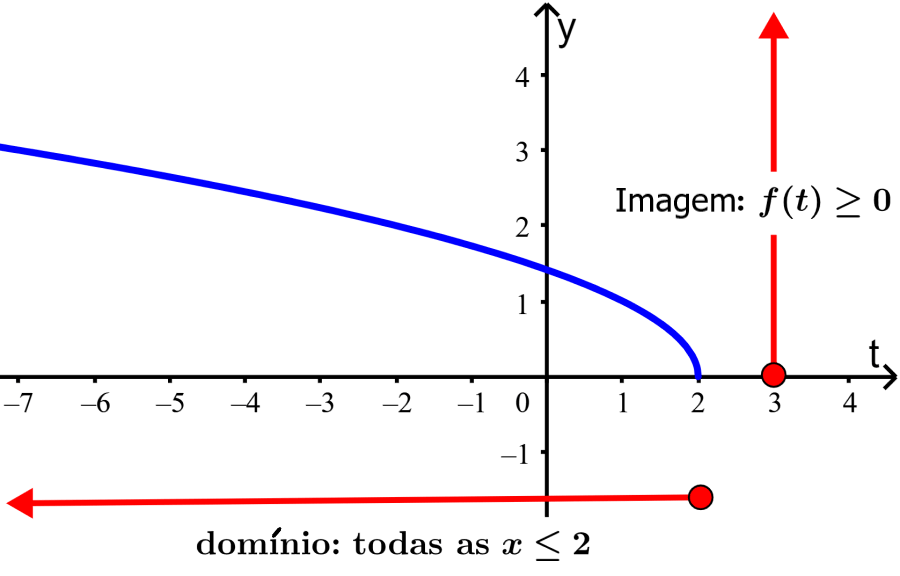
Solução: Vemos que a função se estende indefinidamente para a esquerda e leva valores até 2. Então, seu domínio são todos os números reais de t, onde $latex t \leq 2$.
No caso da imagem, vemos que a função apenas assume valores positivos e se estende para cima indefinidamente. Portanto, a imagem é composta por todos os números reais de $latex f(t)$ e $latex f(t)≥0$.
EXEMPLO 5
Encontre o domínio e a imagem da seguinte função:
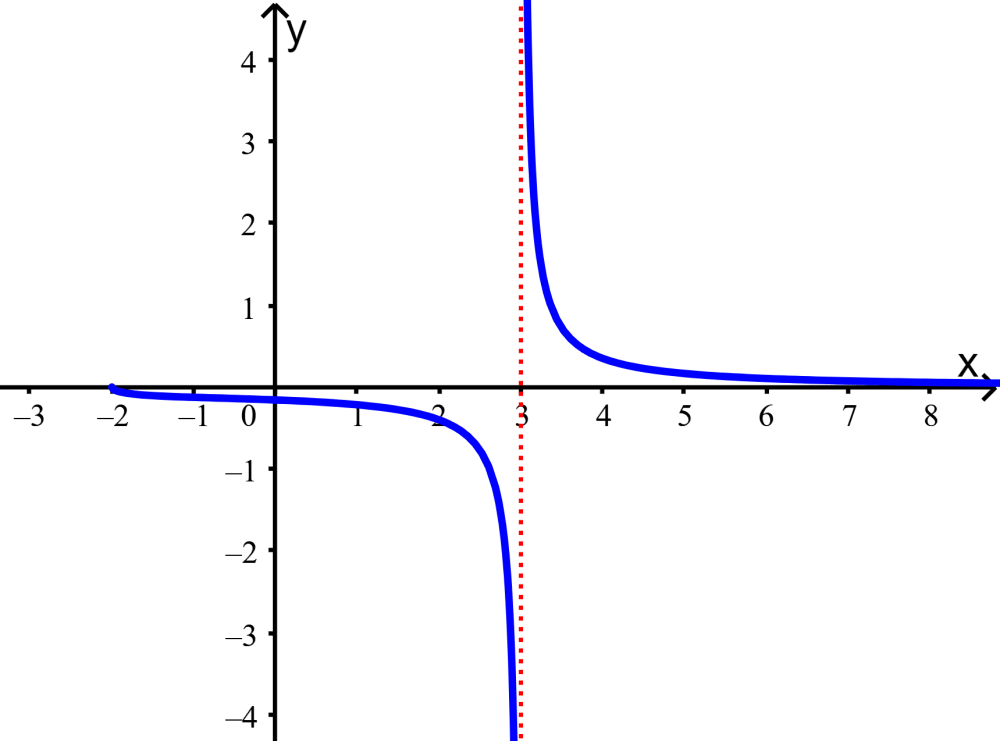
Solução: Podemos ver que esta função possui valores horizontais que começam em $latex x=-2$ e se estendem indefinidamente para a direita. Porém, vemos que a função possui uma assíntota em $latex x=3$, ou seja, a função nunca assume esse valor.
Portanto, o domínio da função são todos os números reais de x, onde $latex x \geq -2$ e $latex x \neq 3$.
No caso da imagem, vemos que o gráfico se estende do infinito negativo ao infinito positivo. Também vemos que, embora pareça que o gráfico nunca resulte em $latex y=0$, podemos ver que a função assume esse valor no ponto $latex x=-2$.
Portanto, a imagem da função são todos os números reais em y.
Veja também
Você quer aprender mais sobre domínio e imagem? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
