Todas as funções trigonométricas são basicamente as proporções trigonométricas de qualquer ângulo dado. Por exemplo, se tomarmos as funções $latex f (x) = \sin(x)$, $latex f(x)= \tan(x)$, etc, estaremos considerando essas proporções trigonométricas como funções. O domínio e a imagem dessas funções trigonométricas dependerão da natureza de suas proporções trigonométricas correspondentes.
A seguir, conheceremos o domínio e a imagem das funções trigonométricas fundamentais, como seno, cosseno e tangente. Além disso, veremos o domínio e a imagem das funções cossecante, secante e tangente.
Domínio e imagem de funções trigonométricas (sin, cos, tan)
Seno
Podemos começar considerando a identidade trigonométrica mais simples:
$latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$
Dessa identidade, podemos derivar as seguintes interpretações:
$latex {{\cos}^2}(x)=1-{{\sin}^2}(x)$
$latex \cos(x)=\sqrt{1-{{\sin}^2}(x)}$
Sabemos que a função cosseno é definida para valores reais, portanto, o valor dentro da raiz quadrada não pode ser negativo. Então, podemos formar a desigualdade:
$latex 1-{{\sin}^2}(x)\geq 0$
$latex {{\sin}^2}(x)\leq 1$
$latex \sin(x)\in [-1, 1]$
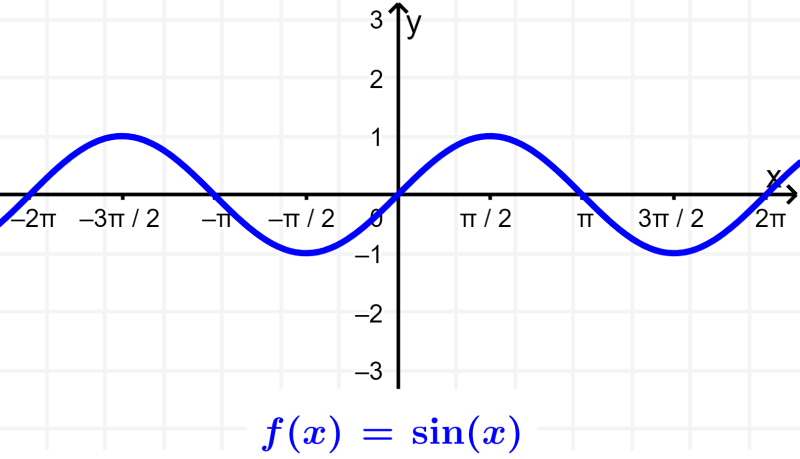
Portanto, já obtivemos o domínio e a imagem para a função seno. O domínio são todos os números reais de x, uma vez que não temos quaisquer restrições aos valores de x. A imagem é de -1 a 1, incluindo esses valores. Podemos verificar isso observando seu gráfico:
Cosseno
Da mesma forma, usando a mesma metodologia, temos:
$latex 1-{{\cos}^2}(x)\geq 0$
$latex {{\cos}^2}(x)\leq 1$
$latex \cos(x)\in [-1, 1]$
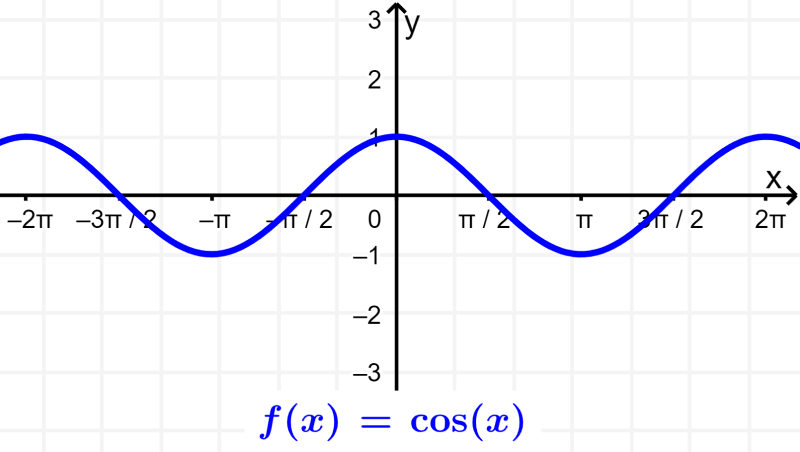
Portanto, o domínio da função cosseno também são todos os números reais de x. A imagem da função cosseno é de -1 a 1, incluindo esses valores. Podemos verificar isso olhando seu gráfico:
Algo importante a se ter em mente é que a imagem de seno e cosseno depende da amplitude das funções. Por exemplo, se tivermos $latex f(x)=5 \cos(x)$, a imagem é de -5 a 5.
Tangente
Agora vamos dar uma olhada na função $latex f(x)=\tan(x)$. Sabemos que $latex \tan(x)=\frac{\sin(x)}{\cos(x)}$. Isso significa que a função tangente é definida para todos os valores, exceto aqueles que tornam $latex \cos(x)$ igual a zero, uma vez que uma fração com denominador igual a zero é indefinida.
Agora, sabemos que $latex \cos(x)$ é zero para os ângulos $latex \frac{\pi}{2},~\frac{3\pi}{2}, ~\frac{5\pi}{2}$, etc.
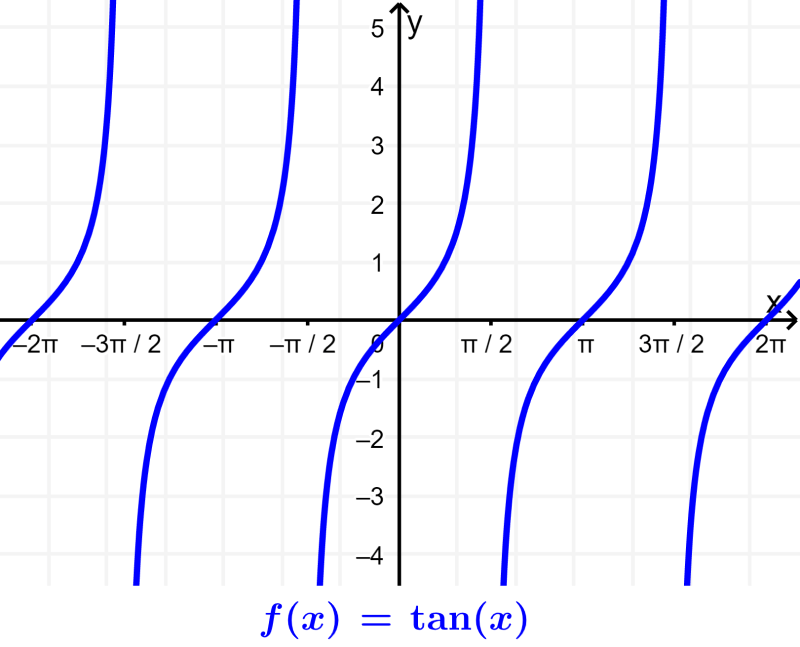
Portanto, o domínio da função tangente é $latex R-\frac{(2n+1)\pi}{2}$ e a imagem é composta por números reais. Podemos ver isso no gráfico:
Domínio e imagem das funções cosec, sec e cot
Secante
Sabemos que a secante é a função recíproca do cosseno. Então nós temos:
$latex \sec(x)=\frac{1}{\cos(x)}$
Isso significa que a secante não será definida para os pontos onde $latex \cos(x)=0$. Portanto, o domínio de $latex f(x)=\sec(x)$ será $latex R-\frac{(2n+1)\pi}{2}$.
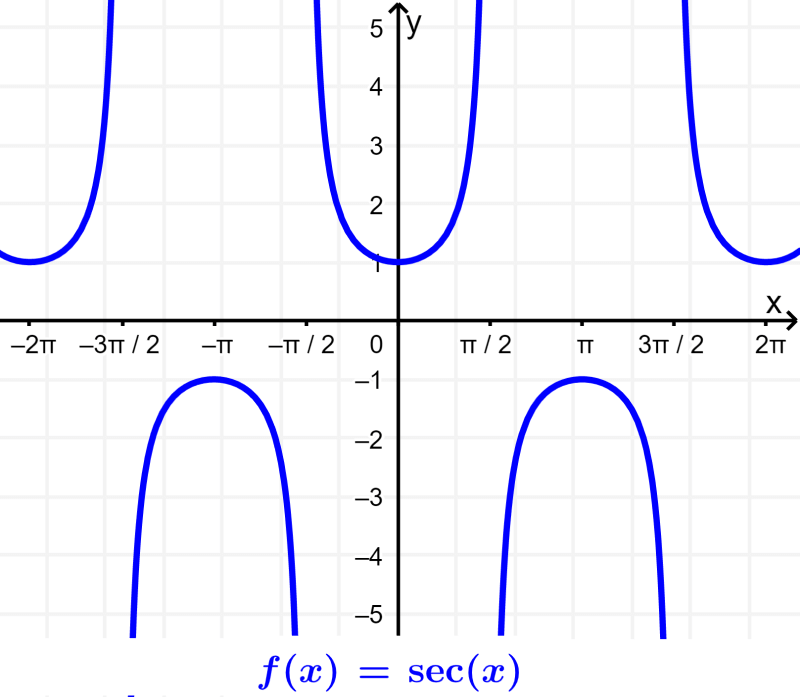
A imagem da secante será $latex R-(-1, 1)$. Uma vez que $latex \cos(x)$ está localizado entre -1 e 1, a secante nunca pode estar nesta região. Podemos olhar para o seu gráfico:
Cossecante
A cossecante é a função recíproca do seno. Então, temos:
$latex \csc(x)=\frac{1}{\sin(x)}$
Sabemos que a cossecante não será definida para os pontos onde $latex \sin(x)=0$. Portanto, o domínio de $latex f(x)=\csc(x)$ será $latex R-n\pi$.
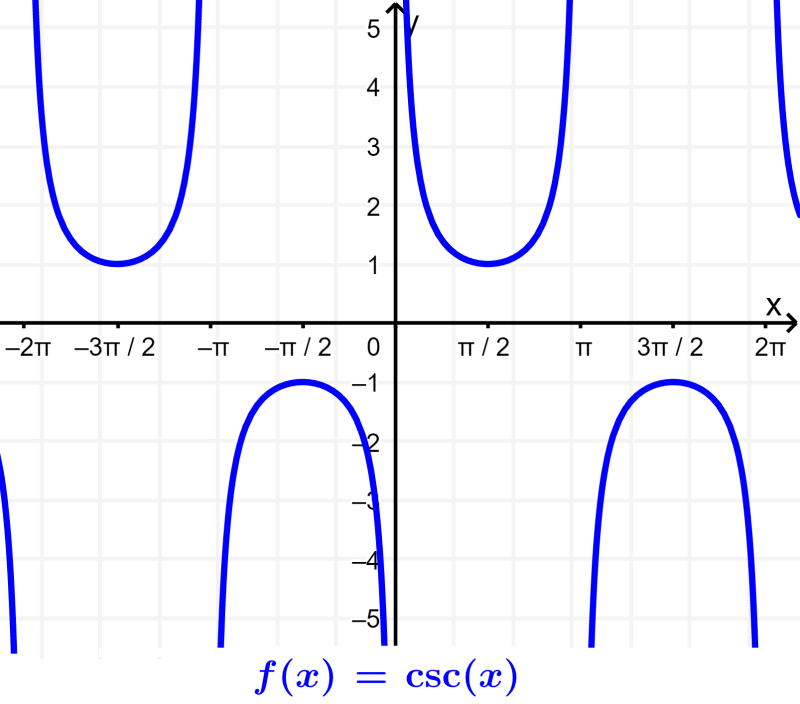
A imagem da cossecante será $latex R – (- 1, 1)$. Isso ocorre porque $latex \sin(x)$ está entre -1 e 1, então a cossecante nunca pode estar nesta região. Podemos verificar com seu gráfico:
Cotangente
A cotangente é a recíproca da tangente. Então, temos:
$latex \cot(x)=\frac{1}{\tan(x)}$
A função cotangente não será definida para os pontos onde $latex \tan(x)=0$. Portanto, o domínio de $latex f(x)=\cot(x)$ será $latex R-n\pi$.
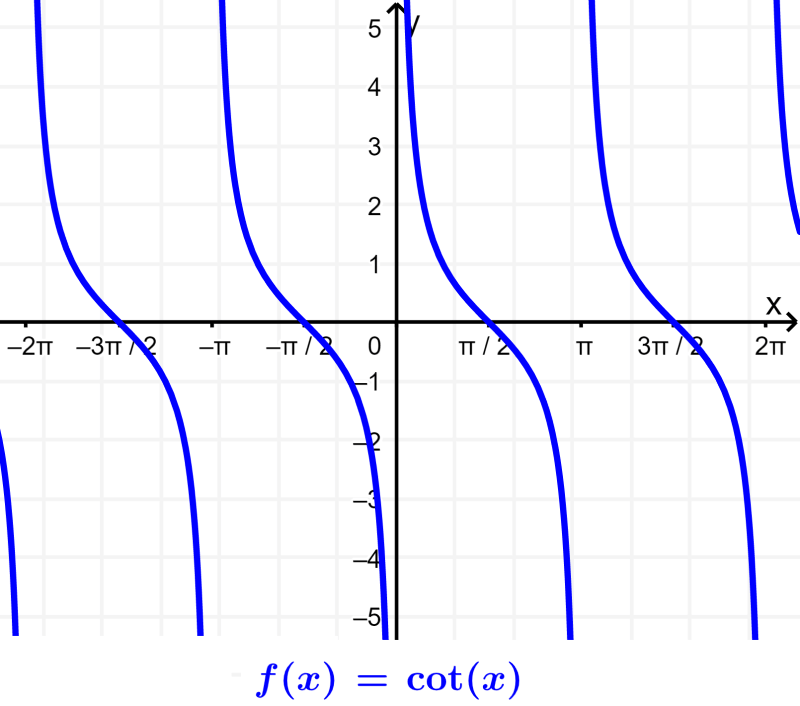
A imagem da cotangente será $latex R-(-1, 1)$ o conjunto de todos os números reais porque não temos restrições. Podemos olhar para o seu gráfico:
Veja também
Você quer aprender mais sobre domínio e imagem? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
