O domínio das funções exponenciais é igual a todos os números reais, uma vez que não temos restrições com os valores que x pode assumir. A imagem de funções exponenciais é igual aos valores acima ou abaixo da assíntota horizontal.
A seguir, veremos em detalhes como encontrar o domínio e a imagem de funções exponenciais. Além disso, veremos vários exemplos com os gráficos das funções para ilustrar essas idéias.
Como encontrar o domínio e a imagem de funções exponenciais?
Lembre-se de que o domínio é o conjunto de valores de entrada usados para a variável independente.
Além disso, lembre-se de que a imagem é o conjunto de todos os valores de saída da variável dependente.
Para qualquer função exponencial com a forma geral $latex f(x) = a{{b}^x}$, o domínio é o conjunto de todos os números reais. Ou seja, temos:
$latex – \infty < x < \infty$
Para qualquer função exponencial com a forma geral $latex f(x)=a{{b}^x}$, a imagem é o conjunto de todos os números reais acima ou abaixo da assíntota horizontal, $latex y=d$. A imagem não inclui o valor da assíntota, d. Ou seja, temos:
Se $latex a>0, ~f(x)>d$
Se $latex a<0, ~f(x)<d$
Exemplos de domínio e imagem de funções exponenciais
EXEMPLO 1
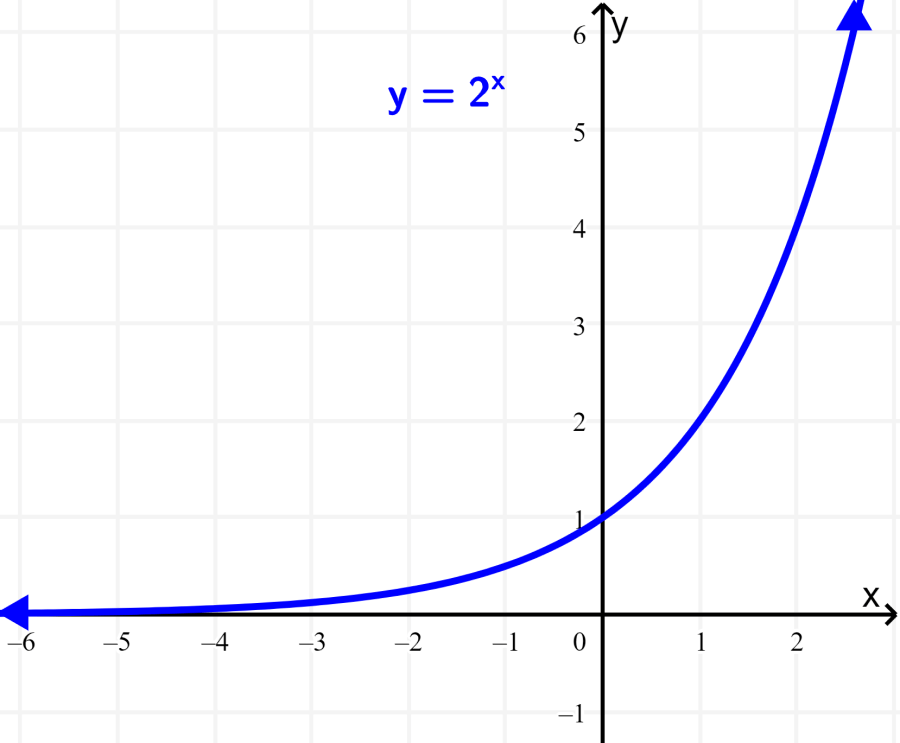
Uma função exponencial simples como $latex f(x)={{2}^x}$ tem um domínio igual a todos os números reais. No entanto, sua imagem é igual apenas a números positivos, onde, $latex y>0$. Ou seja, a função $latex f(x)$ nunca assume um valor negativo.
Além disso, a função nunca atinge o valor 0, embora fique muito próximo quando x se aproxima do infinito negativo.
EXEMPLO 2
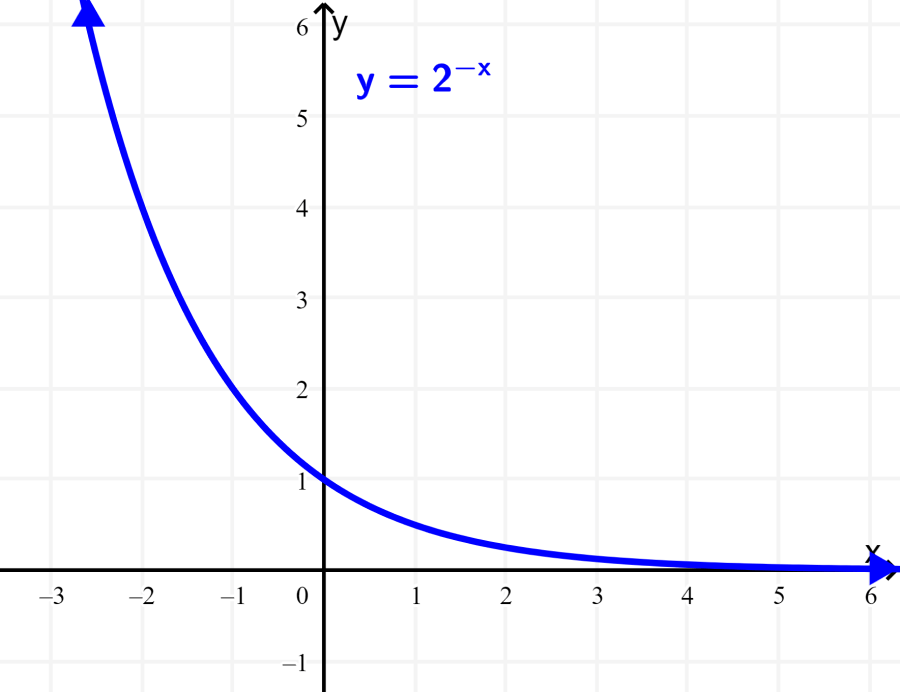
Podemos substituir x por –x na função do exemplo anterior para obter a função $latex g(x)={{2}^{-x}}$. Vemos que o gráfico foi refletido em relação ao eixo y. No entanto, o domínio e a imagem não mudam. O domínio é igual a todos os números reais. E a imagem é igual apenas a números positivos, onde, $latex y>0$.
EXEMPLO 3
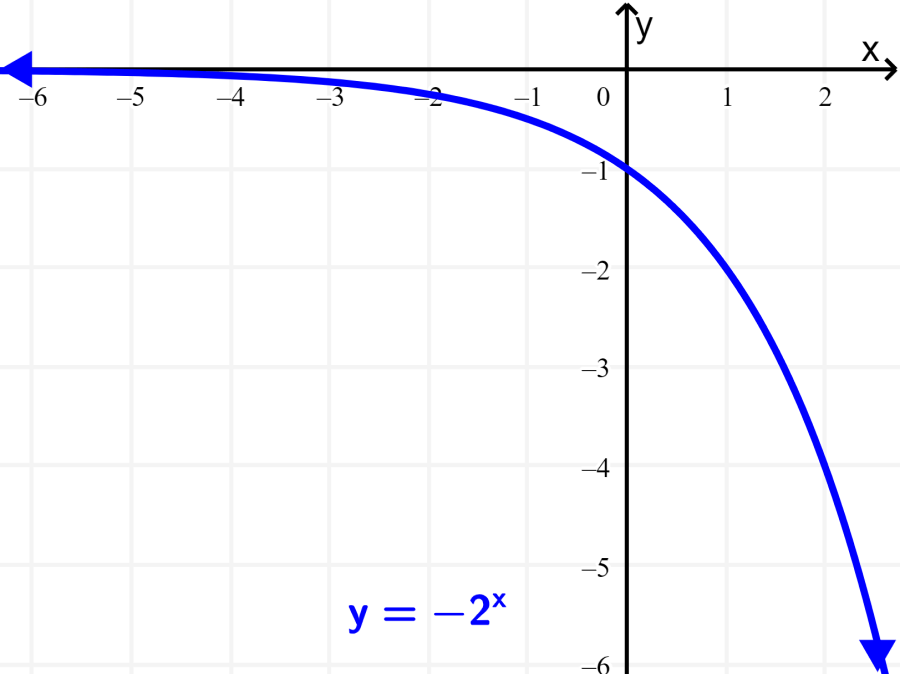
Se pudermos agora colocar um sinal negativo na frente da função, temos $latex h(x)=-{{2}^x}$. Nesse caso, o gráfico é refletido em relação ao eixo x. O domínio ainda é todos os números reais de x. No entanto, a imagem agora é composta de todos os números negativos, onde, $latex y<0$.
EXEMPLO 4
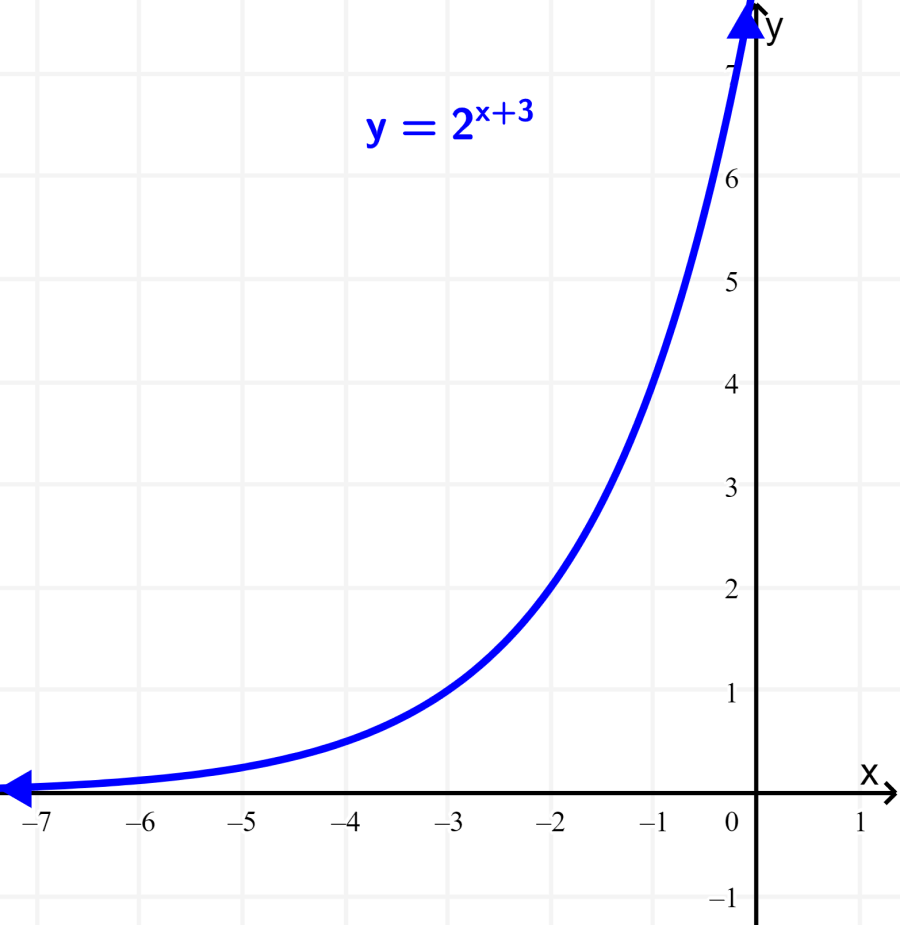
Encontre o domínio e a imagem da função $latex f(x)={{2}^{x + 3}}$
Solução: O gráfico desta função é simplesmente o gráfico de $latex f(x)={{2}^x}$ traduzido 3 unidades para a esquerda.
A função é definida para todos os números reais, portanto, o domínio da função é o conjunto de números reais.
À medida que x se aproxima do infinito, a função também se aproxima do infinito e, à medida que x se aproxima do infinito negativo, a função se aproxima do eixo x, mas nunca o toca.
Portanto, a imagem é o conjunto de todos os números reais $latex \{y \in R | y> 0 \}$.
EXEMPLO 5
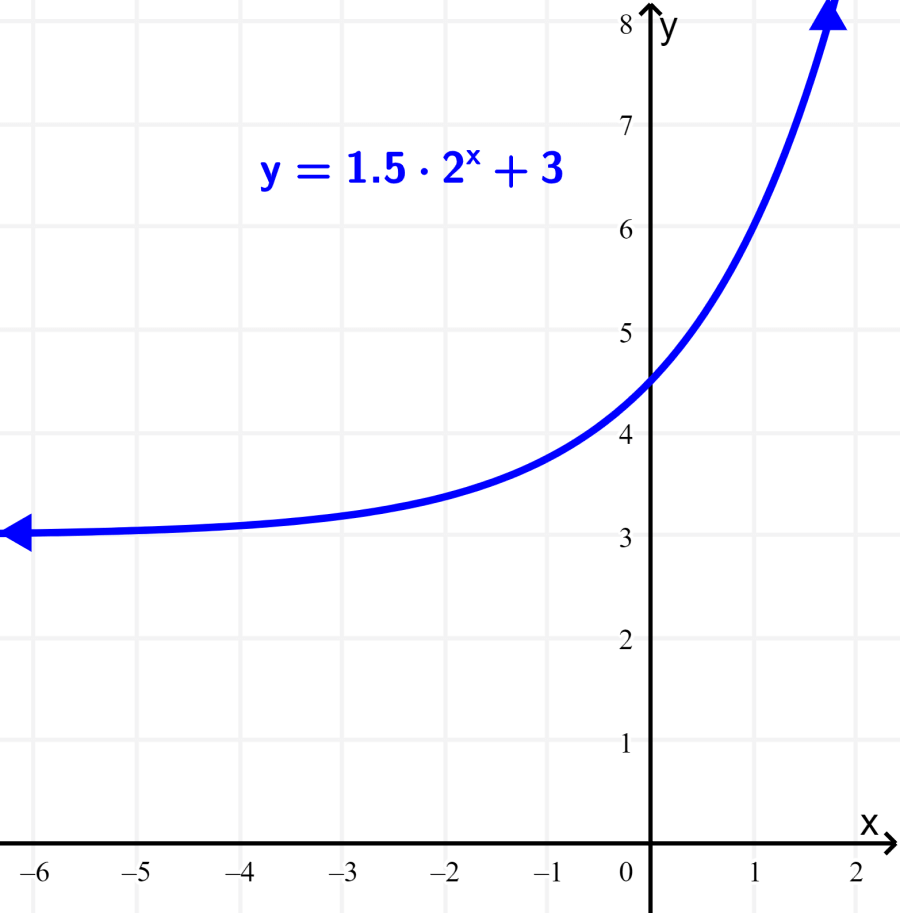
Qual é o domínio e a imagem da função $latex f(x)=1,5({{2}^x})+3$?
Solução: Esta função também é definida para todos os números reais. Portanto, o domínio da função é o conjunto de números reais.
Vemos que, neste caso, $latex d=3$. Isso significa que a assíntota horizontal é igual a $latex y=3$ e a função tem uma imagem igual a todos os números reais maiores que 3.
Portanto, a imagem é o conjunto de todos os números reais $latex \{y \in R | y> 3 \}$.
EXEMPLO 6
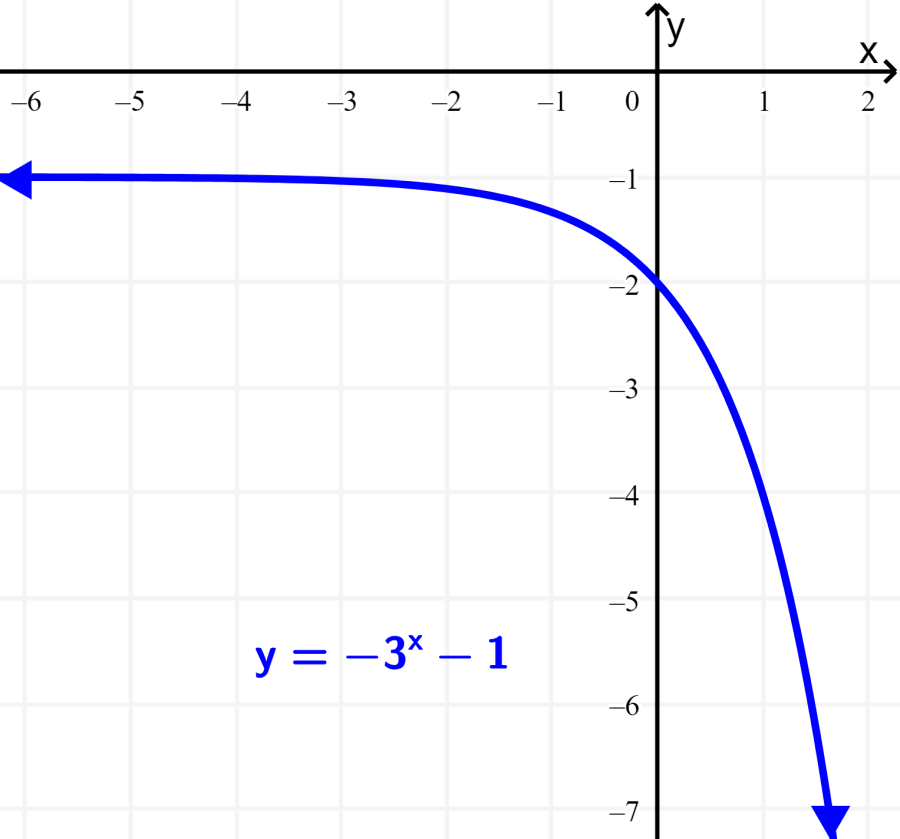
Qual é o domínio e a imagem da função $latex f(x)=-{{3}^x}-1$?
Solução: A função pode aceitar qualquer valor de x como entrada. Isso significa que o domínio é o conjunto de todos os números reais.
A função tem apenas valores negativos de y. Além disso, vemos que temos $latex d=-1$, então a assíntota horizontal é igual a $latex y=-1$. Portanto, a imagem é todos os valores menores que -1.
A imagem é o conjunto de todos os números reais $latex \{y \in R | y <-1 \}$.
Veja também
Você quer aprender mais sobre domínio e imagem? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
