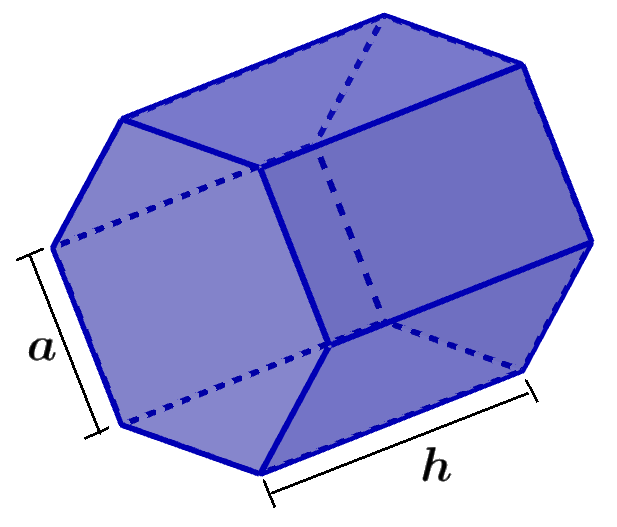
Os prismas hexagonais são figuras tridimensionais, formadas por duas bases hexagonais paralelas. Essas bases são conectadas por seis faces retangulares laterais. Isso significa que, no total, um prisma hexagonal possui 8 faces, duas hexagonais e seis retangulares. Como essas figuras são tridimensionais, elas têm duas propriedades importantes, volume e área.
A seguir, aprenderemos sobre algumas das características mais importantes de um prisma. Além disso, aprenderemos sobre as fórmulas mais utilizadas destes prismas e as utilizaremos para resolver alguns exercícios.
Definição de um prisma hexagonal
Um prisma hexagonal é uma figura 3D que possui duas bases hexagonais paralelas. Essas bases hexagonais são unidas por seis faces retangulares laterais. Os prismas hexagonais têm um total de 8 faces, 12 vértices e 18 arestas.
Os prismas hexagonais podem ser regulares ou irregulares. Um prisma hexagonal regular é um prisma em que suas bases são hexágonos regulares. Os hexágonos regulares têm todos os lados do mesmo comprimento. Esses são os prismas hexagonais mais comuns.
Por outro lado, os prismas hexagonais irregulares são prismas cujas bases são hexágonos irregulares. Os hexágonos irregulares têm lados com comprimentos diferentes e ângulos internos com medidas diferentes.
Características fundamentais do prisma hexagonal
A seguir estão as principais características de um prisma hexagonal:
- Ambas as bases são hexágonos.
- As bases são paralelas entre si.
- Se o prisma for regular, ambas as faces hexagonais são congruentes e têm lados do mesmo comprimento.
- Se o prisma for regular, as seis faces laterais são retângulos congruentes.
- No total, esses prismas têm 8 faces: 2 hexagonais e 6 retangulares.
- Esses prismas têm 12 vértices.
- Esses prismas têm 18 arestas.
Fórmulas importantes do prisma hexagonal
Como os prismas hexagonais são figuras 3D, suas fórmulas mais importantes são a fórmula do volume e a fórmula da área da superfície.
Fórmula do volume do prisma hexagonal
O volume de um prisma hexagonal é igual à área de sua base multiplicada pela altura do prisma. Portanto, temos o seguinte:
| $latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$ |
onde, a representa o comprimento de um dos lados do hexágono e h representa a altura do prisma.
Fórmula do área do prisma hexagonal
A área do prisma hexagonal é calculada somando as áreas de todas as faces do prisma. Temos duas faces hexagonais e duas faces retangulares. A área de ambas as faces retangulares é igual a $latex 3 \sqrt{3}{{a}^2}$ e a área das seis faces retangulares é igual a $latex 6ah$. Então, temos:
| $latex A_{s}=3\sqrt{3}{{a}^2}+6ah$ |
Exemplos de problemas do prisma hexagonal
As fórmulas vistas acima são aplicadas para resolver os seguintes exercícios.
EXEMPLO 1
Um prisma hexagonal tem uma altura de 10 m e sua base tem lados de 5 m de comprimento. Qual é o seu volume?
Solução: Temos os comprimentos $latex h = 10$ e $latex a = 5$. Usamos a fórmula de volume com estes valores, temos:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(5)}^2}(10)$
$latex V=\frac{3\sqrt{3}}{2}(25)(10)$
$latex V=649,5$
O volume é 649,5 m³.
EXEMPLO 2
Qual é o volume de um prisma com 12 m de altura e base hexagonal com lados de 4 m de comprimento?
Solução: Usamos a fórmula do volume com os dados fornecidos:
$latex V=\frac{3\sqrt{3}}{2}{{a}^2}h$
$latex V=\frac{3\sqrt{3}}{2}{{(4)}^2}(12)$
$latex V=\frac{3\sqrt{3}}{2}(16)(10)$
$latex V=415,7$
O volume é de 415,7 m³.
EXEMPLO 3
Qual é a área da superfície de um prisma hexagonal com 8 m de altura e 4 m de comprimento nos lados?
Solução: Usamos a fórmula para área do prisma hexagonal com os valores dados:
$latex A_{s}=3\sqrt{3}{{a}^2}+6ha$
$latex A_{s}=3\sqrt{3}{{(4)}^2}+6(8)(4)$
$latex A_{s}=83,1+192$
$latex A_{s}=275,1$
A área do prisma é de 275,1 m².
EXEMPLO 4
Um prisma hexagonal tem uma altura de 11 m e lados de 6 m de comprimento. Qual é a sua área de superfície?
Solução: Usando a fórmula para área do prisma, temos:
$latex A_{s}=3\sqrt{3}{{a}^2}+6ha$
$latex A_{s}=3\sqrt{3}{{(6)}^2}+6(12)(6)$
$latex A_{s}=187,1+432$
$latex A_{s}=619,1$
A área do prisma é de 619,1 m².
Veja também
Você quer aprender mais sobre prismas hexagonais? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
