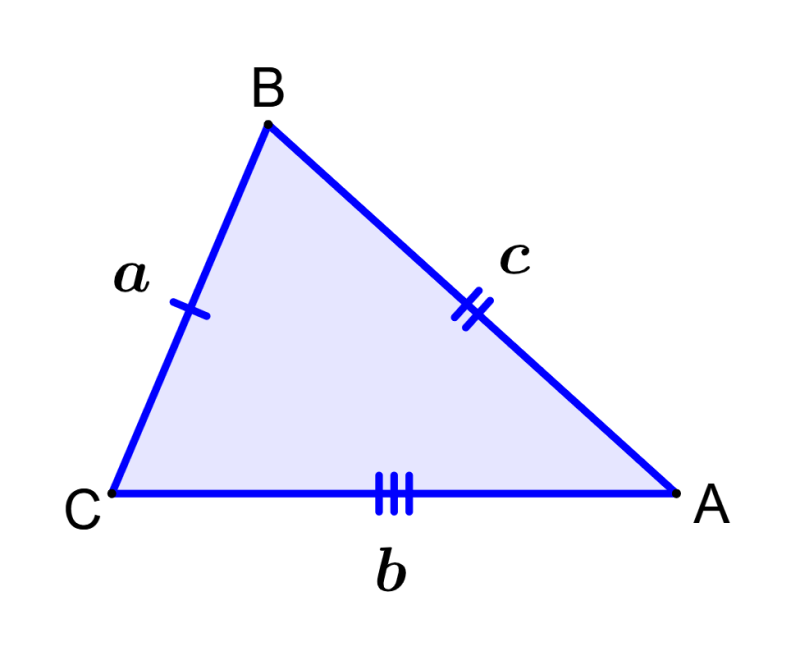
O triângulo escaleno é um triângulo que tem todos os seus lados de comprimentos diferentes. Isso significa que todos os lados do triângulo são desiguais e os três ângulos internos também são desiguais. Este é um dos três tipos de triângulos baseados nos lados.
A seguir, veremos a definição de triângulos escalenos, conheceremos suas fórmulas mais importantes e aprenderemos sobre suas propriedades fundamentais. Além disso, veremos também alguns exemplos nos quais aplicaremos as fórmulas do triângulo escaleno.
GEOMETRIA
Relevante para…
Aprender sobre as características do triângulo escaleno.
GEOMETRIA
Relevante para…
Aprender sobre as características do triângulo escaleno.
Definição do triângulo escaleno
Um triângulo escaleno é um triângulo em que os três lados têm comprimentos diferentes e os três ângulos têm medidas diferentes. No entanto, a soma dos ângulos internos é sempre igual a 180 graus, portanto, está de acordo com a propriedade da soma dos ângulos internos dos triângulos.
Características do triângulo escaleno
Algumas das características mais importantes dos triângulos escalenos são as seguintes:
- O triângulo escaleno não tem lados iguais, todos os seus lados são diferentes uns dos outros.
- O triângulo escaleno não tem ângulos iguais, todos os seus ângulos são diferentes uns dos outros.
- Esses triângulos não têm linhas de simetria.
- Eles não têm simetria com respeito a nenhum ponto.
- Os ângulos internos podem ser agudos, obtusos ou retos.
- Se os ângulos do triângulo forem menores que 90 graus, o centro do círculo circunscrito estará localizado dentro do triângulo.
- Um triângulo escaleno pode ser um triângulo retângulo obtuso ou agudo.
Fórmulas importantes do triângulos escalenos
A seguir estão as fórmulas de área e perímetro que podem ser úteis na solução de problemas envolvendo triângulos escalenos.
Área de um triângulo escaleno
Se sabemos o comprimento da base e o comprimento da altura do triângulo, podemos usar a seguinte fórmula:
| $latex A=\frac{1}{2}\times b \times h$ |
onde, b representa o comprimento da base e h representa o comprimento da altura.
Se conhecermos os comprimentos dos três lados do triângulo, podemos usar a fórmula de Heron:
| $latex A=\sqrt{S(S-a)(S-b)(S-c)}$ |
onde, $latex a, ~b, ~c$ são os comprimentos dos lados e $latex S$ é o semiperímetro, que pode ser encontrado usando a seguinte fórmula:
$latex S=\frac{a+b+c}{2}$
Perímetro do triângulo escaleno
O perímetro de um triângulo é igual à soma dos comprimentos de todos os seus lados. Então, temos a fórmula:
| $latex p=a+b+c$ |
onde, $latex a,~b,~c$ representam os comprimentos dos lados do triângulo.
Exemplos de problemas do triângulos escalenos
EXEMPLO 1
- Um triângulo tem uma base de 14 m e uma altura de 10 m. Qual é a sua área?
Solução: Usamos a fórmula de área para resolver isso:
$latex A=\frac{1}{2}\times b\times h$
$latex A=\frac{1}{2}\times 14\times 10$
$latex A=70$
A área é 70 m².
EXEMPLO 2
- Um triângulo tem lados de comprimentos de 8 m, 10 m e 12 m. Qual é a sua área?
Solução: Usamos a fórmula de Heron para resolver:
$latex A=\sqrt{S(S-a)(S-b)(S-c)}$
Primeiro, temos que encontrar o semiperímetro. Então, usamos a seguinte fórmula:
$latex S=\frac{a+b+c}{2}$
$latex S=\frac{8+10+12}{2}$
$latex S=15$
Agora, resolvemos para a área com os valores que temos:
$latex A=\sqrt{S(S-a)(S-b)(S-c)}$
$$A=\sqrt{15(15-8)(15-10)(15-12)}$$
$latex A=\sqrt{15(7)(5)(3)}$
$latex A=\sqrt{1575}$
$latex A=39.7$
A área é 39.7 m².
EXEMPLO 3
- Temos um triângulo com lados de comprimentos de 11 m, 15 m e 16 m. Qual é o seu perímetro?
Solução: Usamos a fórmula do perímetro com esses comprimentos:
$latex p=a+b+c$
$latex p=11+15+16$
$latex p=42$
O perímetro é de 42 m.
Veja também
Você quer aprender mais sobre triângulos escalenos? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
