As operações vetoriais, além de permitir uma conexão entre a geometria e a álgebra, servem como espinha dorsal para várias disciplinas, como computação gráfica, engenharia e ciência de dados.
Em seguida, aprenderemos os conceitos básicos das operações vetoriais. Exploraremos a adição, a multiplicação escalar e os produtos escalares e cruzados, que juntos fornecem um conjunto completo de ferramentas matemáticas úteis.
Adição e subtração de vetores
Dois ou mais vetores podem ser somados ou subtraídos usando métodos gráficos ou algébricos. Graficamente, podemos adicionar vetores usando o método do polígono e o método do paralelogramo.
Algebricamente, podemos adicionar ou subtrair vetores usando seus componentes.
Adição e subtração de vetores com o método do polígono
Para adicionar dois vetores $latex \vec{A}$ e $latex \vec{B}$ com o método do polígono, colocamos a base de um dos vetores na cabeça ou ponta do outro vetor:
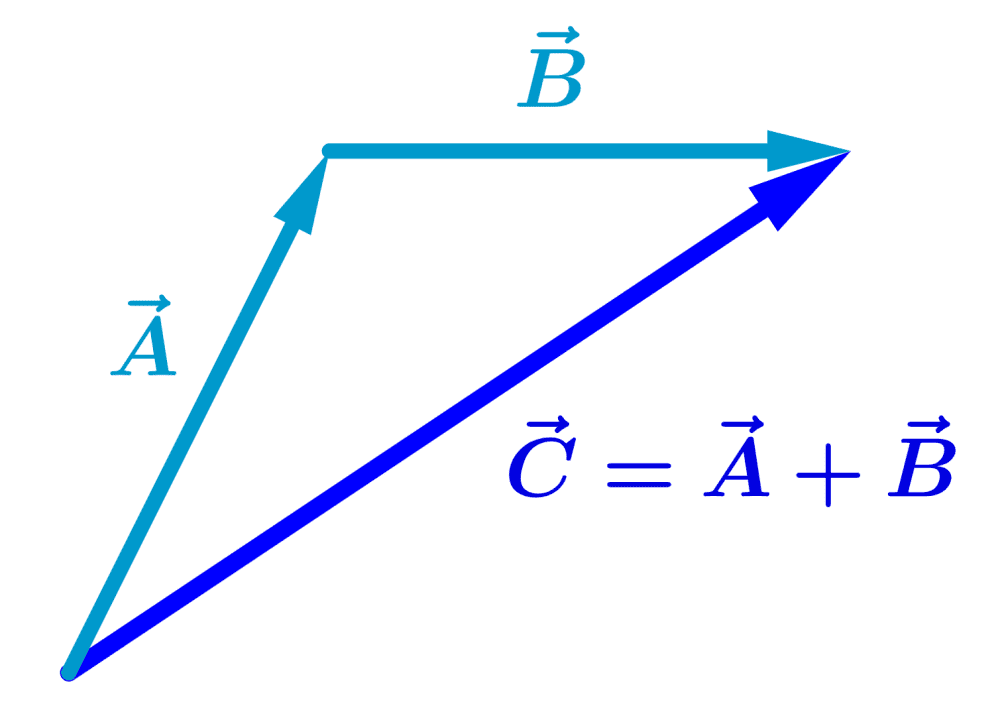
O vetor $latex \vec{C}$ é a soma dos vetores $latex \vec{A}$ e $latex \vec{B}$ e é expresso simbolicamente como:
$latex \vec{C}=\vec{A}+\vec{B}$
Se adicionarmos os vetores na ordem inversa, ou seja, $latex \vec{B}$ primeiro e $latex \vec{A}$ depois, o resultado será o mesmo:
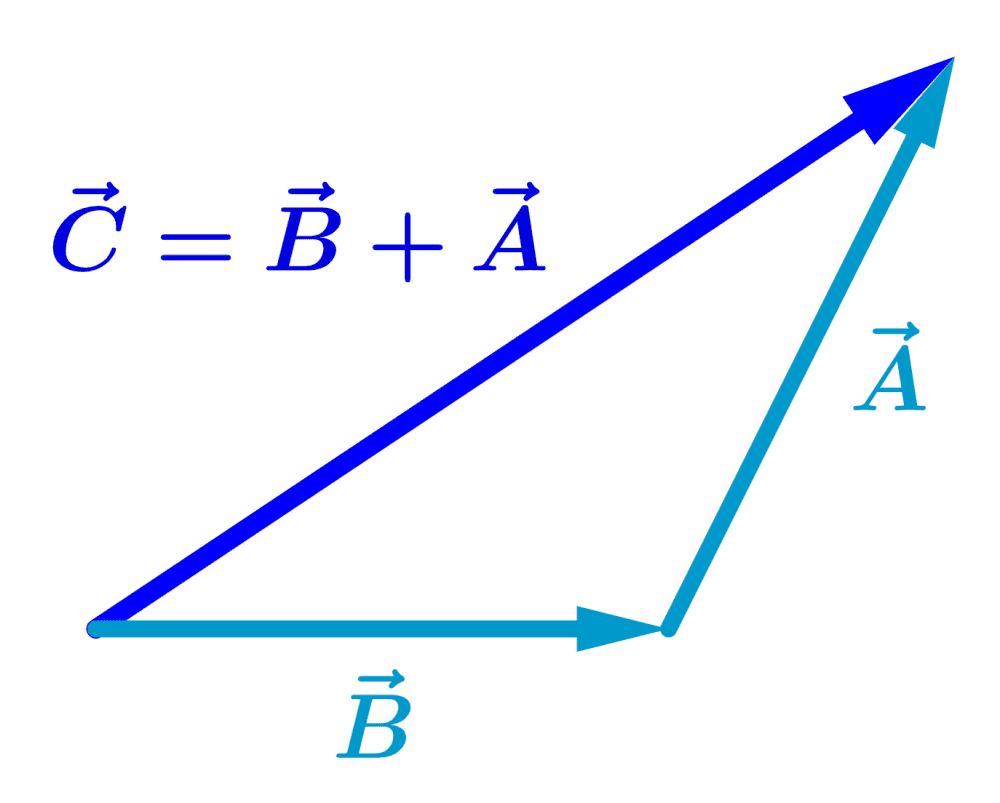
Para subtrair um vetor de outro vetor, temos de mudar a direção do vetor que estamos subtraindo. Por exemplo, para resolver $latex \vec{A}-\vec{B}$, mudamos a direção do vetor $latex \vec{B}$.
No exemplo acima, isso significaria mudar a direção do vetor da seguinte forma:
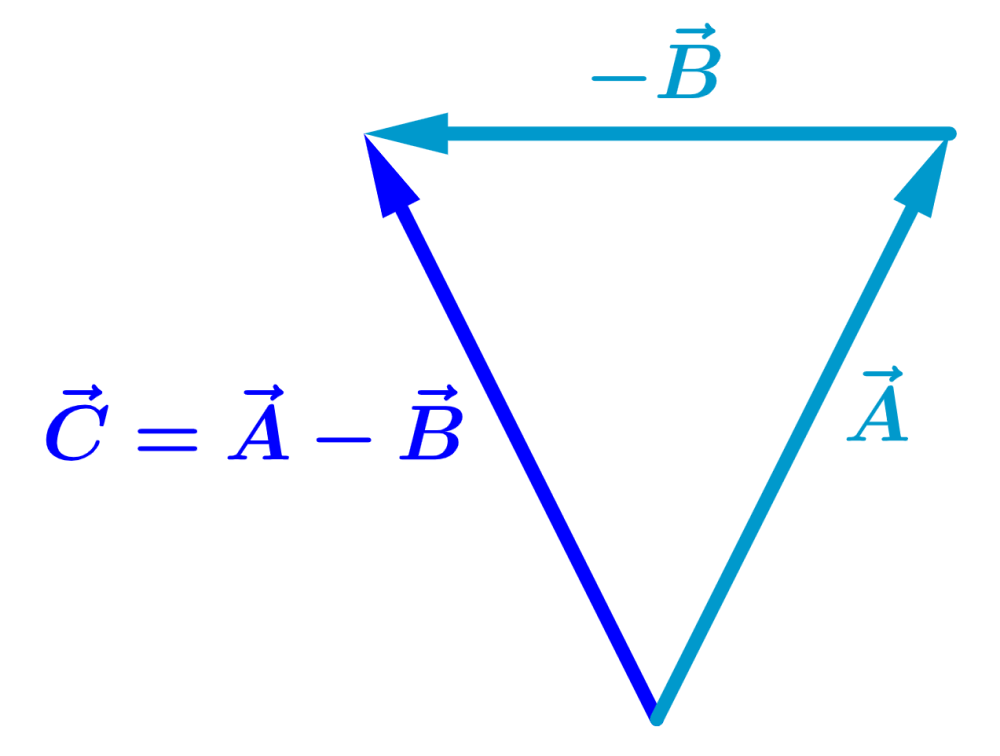
Adição e subtração de vetores com o método do paralelogramo
Para adicionar vetores com esse método, colocamos os vetores com suas bases no mesmo ponto. Em seguida, desenhamos um paralelogramo no qual os vetores são dois lados adjacentes.
Por exemplo, o diagrama a seguir representa a soma dos vetores $latex \vec{A}$ e $latex \vec{B}$:
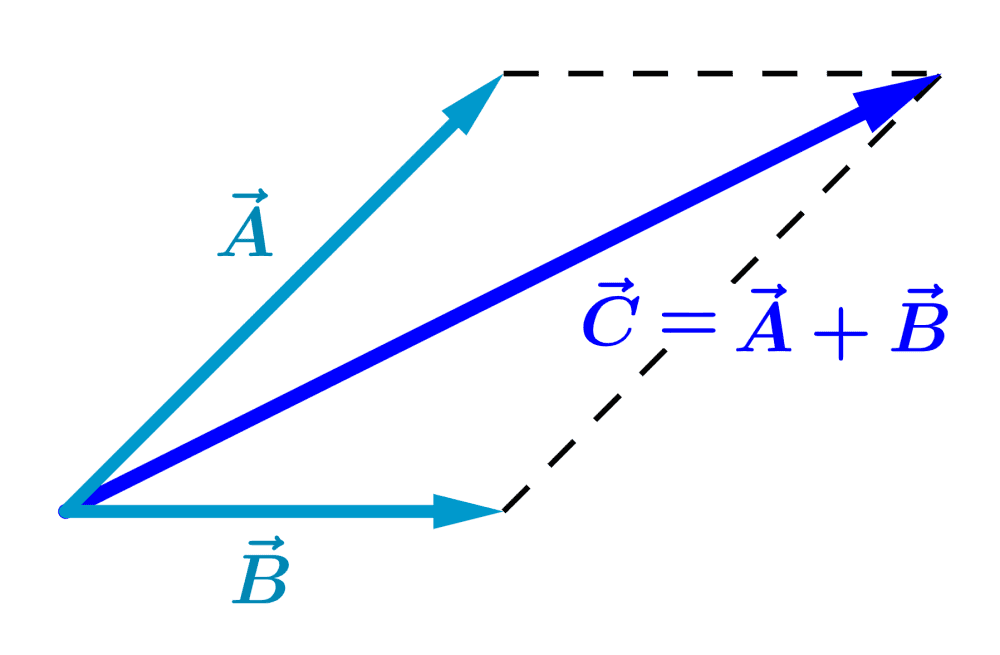
Vemos que o resultado da soma, o vetor $latex \vec{C}$, é a diagonal do paralelogramo.
Semelhante ao método anterior, para subtrair os vetores, mudamos a direção do vetor que está sendo subtraído.
Adição ou subtração de vetores usando seus componentes
Quando conhecemos os componentes dos vetores a serem adicionados ou subtraídos, podemos simplesmente adicionar ou subtrair seus componentes separadamente.
Suponha que tenhamos os seguintes vetores $latex \vec{A}$ e $latex \vec{B}$:
$latex \vec{A}=A_{x}+A_{y}+A_{z}$
$latex \vec{B}=B_{x}+B_{y}+B_{z}$
Para encontrar a soma $latex \vec{C}=\vec{A}+\vec{B}$, basta adicionar seus componentes:
$latex C_{x}=A_{x}+B_{x}$
$latex C_{y}=A_{y}+B_{y}$
$latex C_{z}=A_{z}+B_{z}$
Da mesma forma, simplesmente subtraímos seus componentes quando temos uma subtração de vetor.
EXEMPLO 1
Use o método do polígono para adicionar os seguintes vetores:
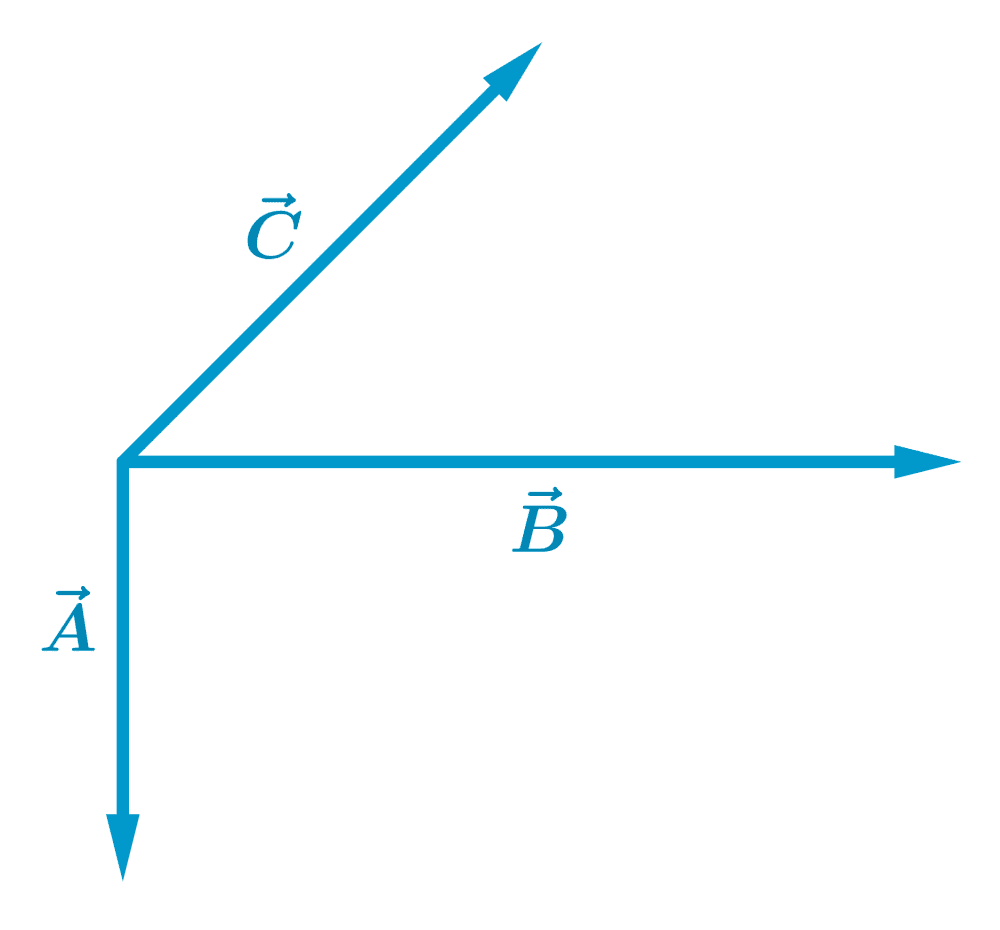
Solução
Podemos começar somando os vetores $latex \vec{A}$ e $latex \vec{B}$ para obter o vetor $latex \vec{D}$:
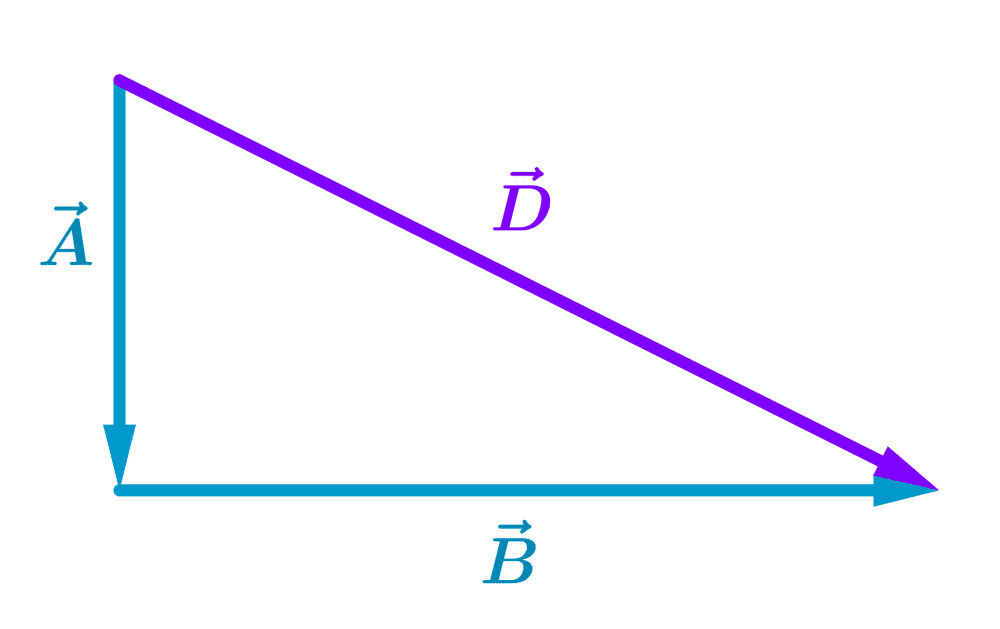
Agora, vamos adicionar o vetor $latex \vec{C}$ ao vetor $latex \vec{D}$ para obter o resultado $latex \vec{R}$:
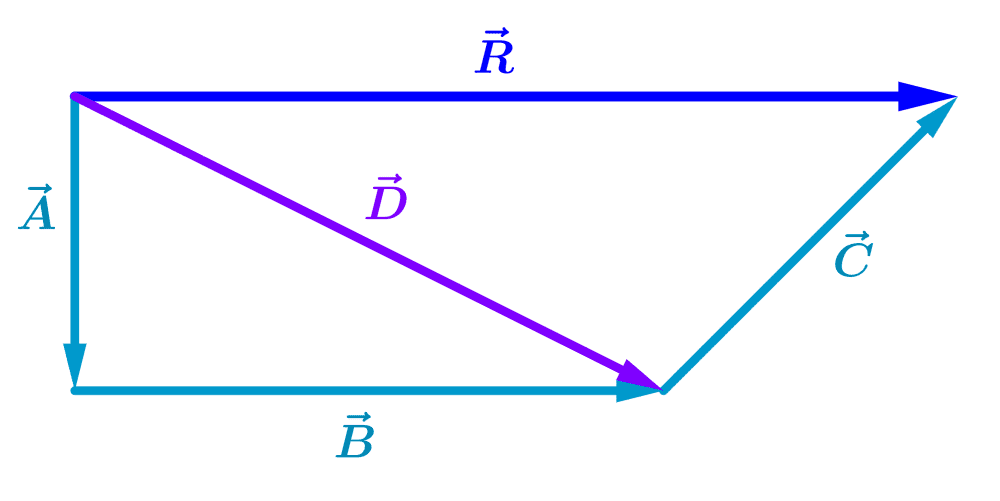
.
EXEMPLO 2
Adicione os vetores a seguir usando o método do paralelogramo:
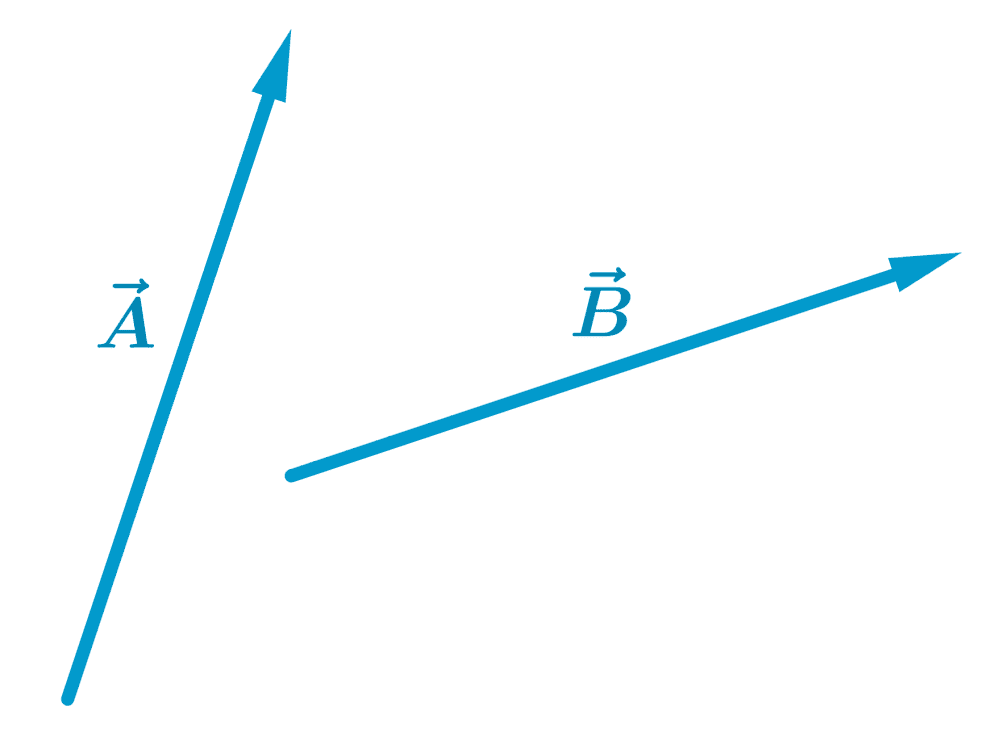
Solução
Colocamos as bases dos vetores no mesmo ponto e formamos um paralelogramo, no qual os vetores são lados adjacentes:
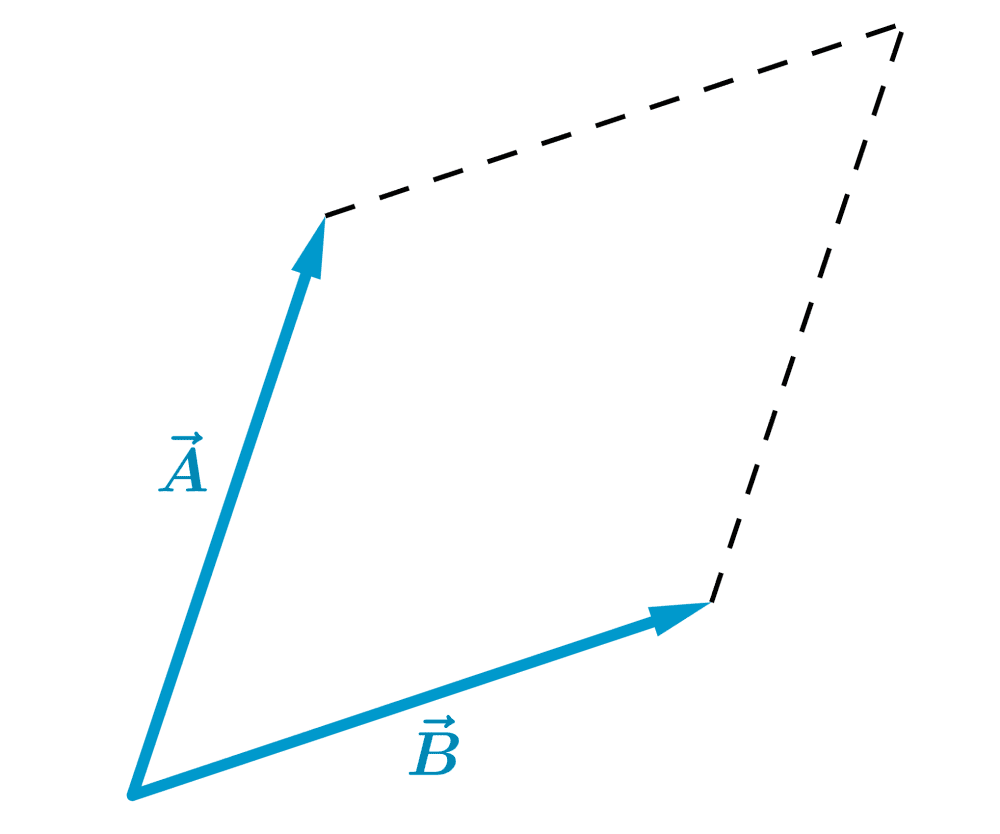
A soma dos vetores é igual à diagonal do paralelogramo formado:
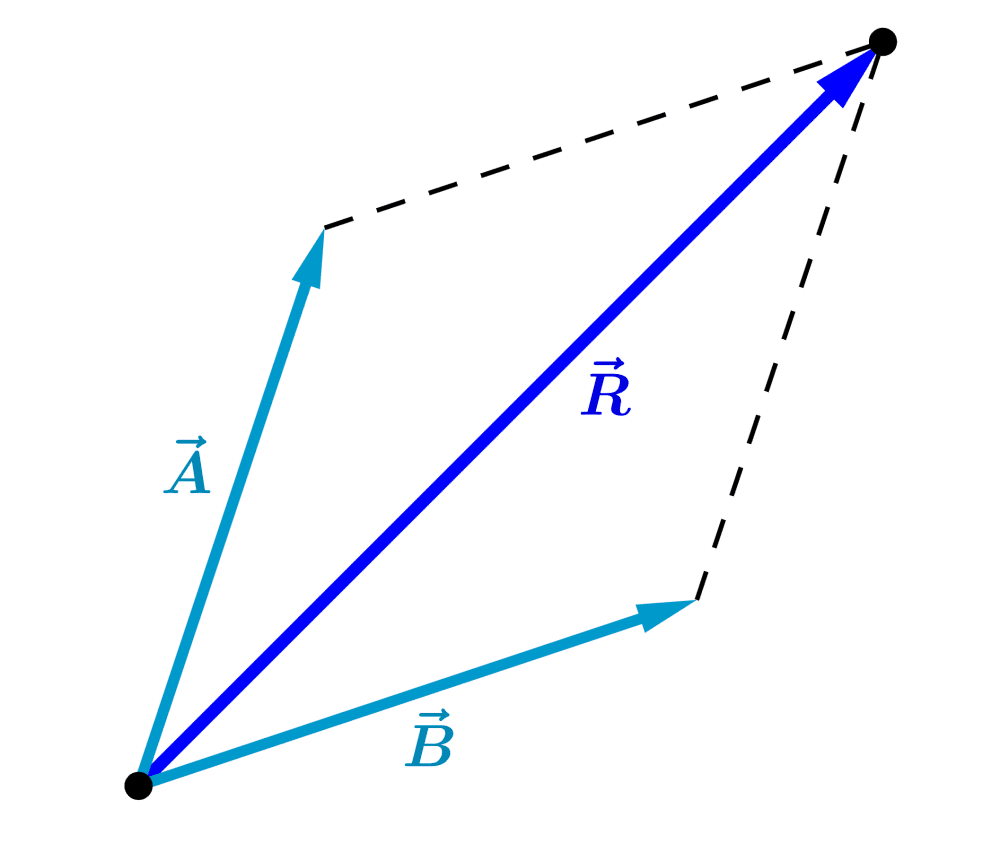
.
EXEMPLO 3
Adicione os vetores $latex \vec{A}=3i+2j+5k$ e $latex \vec{B}=2i+j+3k$.
Solução
Nessa notação, os vetores unitários $latex i, ~j,~ k$ representam as coordenadas $latex x,~ y,~ z$, respectivamente.
Em seguida, basta adicionar os componentes correspondentes de $latex \vec{A}$ e $latex \vec{B}$ para encontrar a soma dos vetores:
$$R_{x}=A_{x}+B_{x}=3+2=5$$
$$R_{y}=A_{y}+B_{y}=2+1=3$$
$$R_{z}=A_{z}+B_{z}=5+3=8$$
Então, a soma dos vetores é
$latex \vec{R}=5i+3j+8k$
Multiplicação de vetores por um escalar
A multiplicação de vetores por um escalar é facilmente resolvida pela multiplicação da magnitude do vetor ou de seus componentes pelo escalar.
A multiplicação de vetores por um escalar positivo afeta a magnitude do vetor, mas não sua direção:
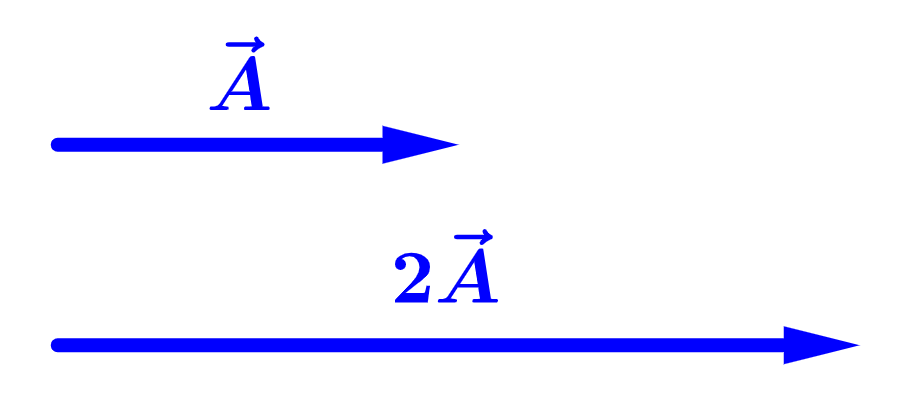
Entretanto, quando multiplicamos por um escalar negativo, sua direção é invertida:
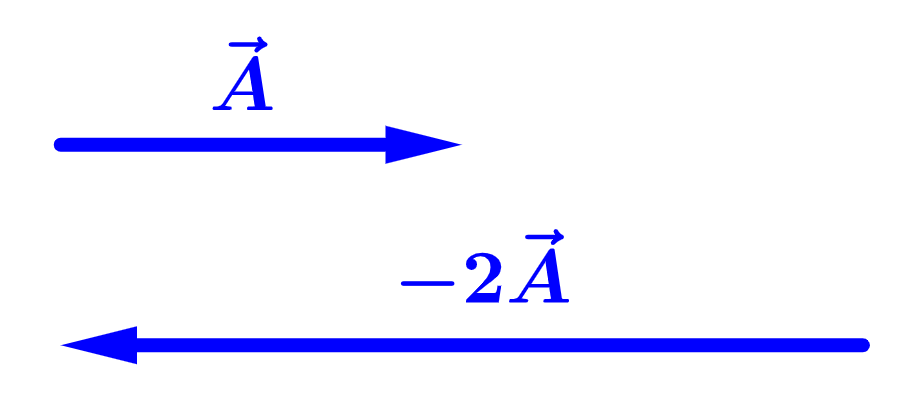
Para um vetor $latex \vec{A}$ com componentes $latex A_{x}$ e $latex A_{y}$, a multiplicação por um escalar $latex k$ é igual a:
$latex R_{x}=kA_{x}$
$latex R_{y}=kA_{y}$
EXEMPLO
Multiplique o vetor $latex \vec{D} = 2i -5j+ 4k$ pelo escalar $latex k = 3$.
Solução
Para resolver essa multiplicação, multiplicamos cada componente do vetor $latex \vec{D}$ pelo escalar $latex k$:
$latex 2i \times 3 = 6i$
$latex -5j \times 3 = -15j$
$latex 4k \times 3 = 12k$
O vetor resultante é: $latex \vec{R}= 6i -15j+ 12k$.
Produto escalar de vetores
O produto escalar de dois vetores $latex \vec{A}$ e $latex \vec{B}$ é denotado por $latex \vec{A} \cdot \vec{B}$. O resultado do produto escalar é uma quantidade escalar.
Podemos calcular o produto escalar usando as magnitudes ou componentes dos vetores.
Produto escalar usando magnitudes e ângulos entre vetores
Quando conhecemos as magnitudes dos vetores e o ângulo entre suas direções, podemos aplicar a seguinte fórmula:
$$\vec{A}\cdot \vec{B}=AB\cos(\theta)$$
onde, $latex A$ e $latex B$ são as magnitudes de $latex \vec{A}$ e $latex \vec{B}$ respectivamente, e $latex \theta$ é o ângulo entre os vetores.
Produto escalar de vetores usando seus componentes
Quando soubermos os componentes $latex x,~y,~z$ dos vetores, poderemos aplicar a seguinte fórmula:
$$\vec{A}\cdot \vec{B}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{z}$$
Você pode ver as demonstrações dessas fórmulas neste artigo: Fórmulas e propriedades do produto escalar vetorial.
EXEMPLO 1
Encontre o produto escalar dos vetores A e B, que têm magnitudes 4 e 6, respectivamente, e o ângulo entre eles é de 120°.
Solução
Temos as seguintes informações:
- $latex |A|=4$
- $latex |B|=6$
- $latex \theta=120^{\circ}$
Usando a fórmula fornecida acima, temos:
$latex \vec{A} \cdot \vec{B} = |A| ~|B| \cos(\theta)$
$latex = 4 \times 6 \cos(120^{\circ}) $
$$= 24 \left(-\frac{1}{2}\right) $$
$$= -12$$
EXEMPLO 2
Temos os vetores $latex \vec{A} = \langle -3,~ 7,~ 1\rangle$ e $latex \vec{B} = \langle 5, ~2,~ 4\rangle$. Qual é o seu produto escalar?
Solução
Nesse caso, temos os componentes dos vetores, portanto, usamos a seguinte fórmula:
$latex \vec{A} \cdot \vec{B} = A_{x} \times B_{x} + A_{y} \times B_{y} + A_z \times B_{z}$
$latex \vec{A} \cdot \vec{B} = (-3 \times 5) + (7 \times 2) + (1 \times 4)$
$latex = -15 + 14 + 4 $
$latex = 3$
Produto vetorial de vetores
O produto vetorial de dois vetores $latex \vec{A}$ e $latex \vec{B}$ é denotado por $latex \vec{A} \times \vec{B}$. O resultado do produto vetorial é um vetor.
O produto vetorial pode ser calculado usando as magnitudes e o ângulo entre os vetores ou usando os componentes dos vetores.
Produto vetorial usando magnitudes e ângulos entre vetores
Se soubermos as magnitudes dos vetores e o ângulo entre eles, calcularemos a magnitude de seu produto vetorial com a seguinte fórmula:
$$\vec{A}\times \vec{B}=AB\sin(\theta)$$
onde, $latex A$ e $latex B$ são as magnitudes de $latex \vec{A}$ e $latex \vec{B}$ respectivamente, e $latex \theta$ é o ângulo entre os vetores.
Direção do produto vetorial.
A direção do produto vetorial é perpendicular a ambos os vetores, $latex \vec{A}$ e $latex \vec{B}$. Podemos encontrar sua direção usando a regra da mão direita.
Com nossa mão direita, giramos do vetor $latex \vec{A}$ para a direção do vetor $latex \vec{B}$. Os dedos devem apontar na direção da rotação:
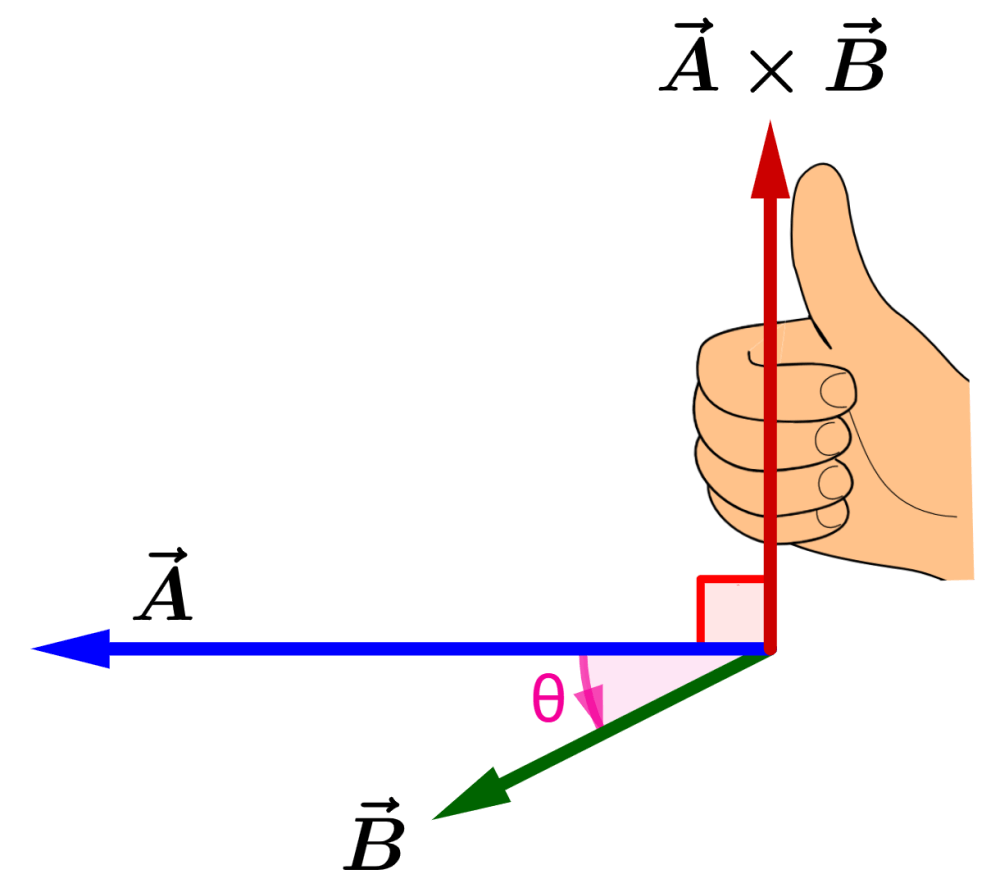
O polegar mostra a direção do $latex \vec{A}\times \vec{B}$.
A direção de $latex \vec{B}\times \vec{A}$ é encontrada pela rotação do vetor $latex \vec{A}$ para a direção do vetor $latex \vec{B}$:
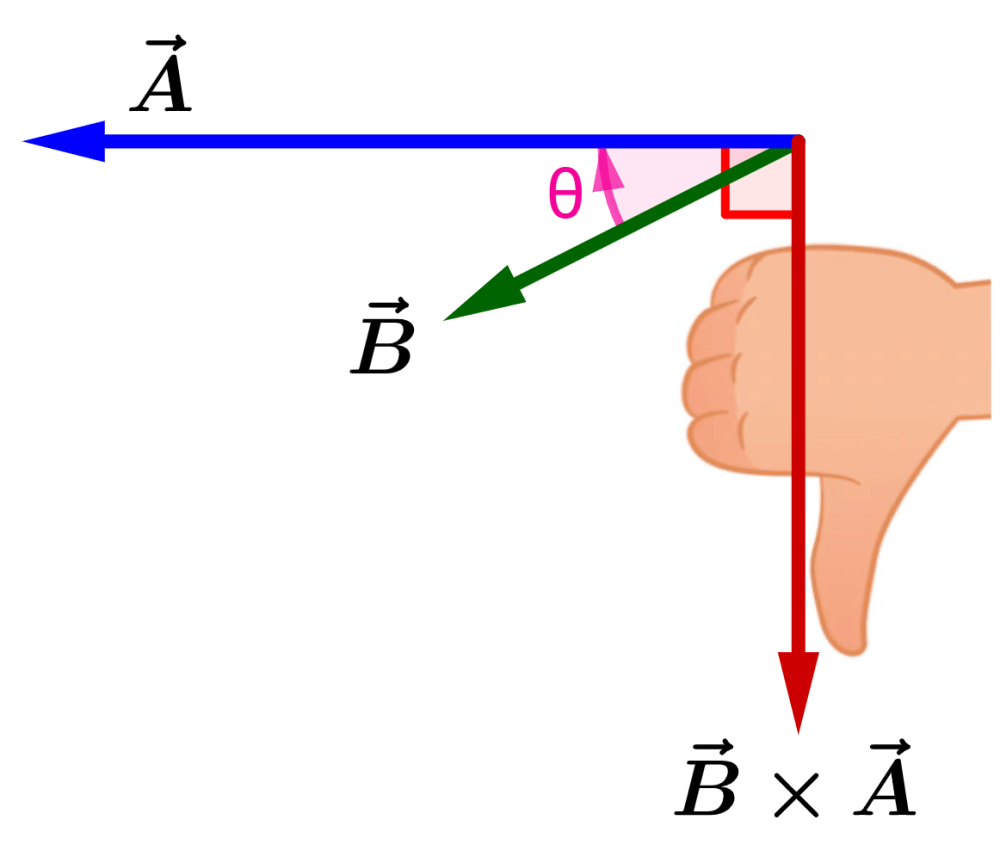
No produto vetorial, $latex \vec{B}\times \vec{A}$ é o oposto de $latex \vec{A}\times \vec{B}$. Ou seja, temos:
$latex \vec{A}\times \vec{B}=-\vec{B}\times \vec{A}$
Produto vetorial de vetores usando seus componentes
Quando soubermos os componentes dos vetores, poderemos calcular o produto vetorial $latex \vec{A} \cdot \vec{B}$ usando a seguinte fórmula:
$latex C_{x}=A_{y}B_{z}-A_{z}B_{y}$
$latex C_{y}=A_{z}B_{x}-A_{x}B_{z}$
$latex C_{z}=A_{x}B_{y}-A_{y}B_{x}$
Você pode ler sobre as demonstrações dessas fórmulas neste artigo: Fórmulas e propriedades do produto vetorial de vetores.
EXEMPLO 1
Um vetor $latex \vec{A}$ tem uma magnitude de 8 unidades na direção de $latex +x$. O vetor $latex \vec{B}$ tem uma magnitude de 6 unidades e está no plano $latex xy$ fazendo um ângulo de 30° com o eixo $latex +x$.
O que é o produto vetorial $latex \vec{C}=\vec{A}\times \vec{B}$?
Solução
Como conhecemos as magnitudes dos vetores e o ângulo entre suas direções, podemos usar a seguinte fórmula para encontrar a magnitude do vetor $latex \vec{C}$:
$latex C=AB\sin(\theta)$
$latex =(8)(6)\sin(30^{\circ})$
$latex =24$
Agora, usamos a regra da mão direita no diagrama a seguir para encontrar a direção do vetor $latex \vec{C}$:
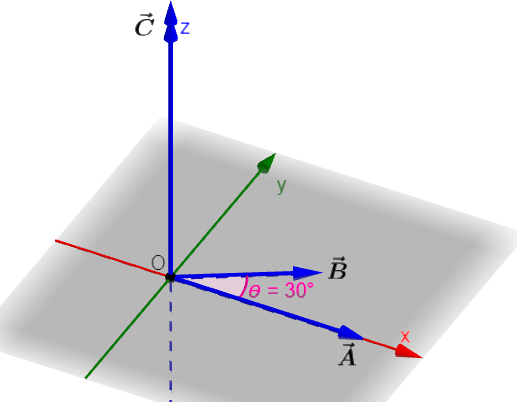
Pela regra da mão direita, a direção de $latex \vec{A}\times \vec{B}$ é ao longo de $latex +z$ ou na direção $latex \hat{k}$. Então,
$latex \vec{C}=\vec{A}\times \vec{B}=24\hat{k}$
EXEMPLO 2
Se tivermos os vetores dados abaixo, qual é o produto vetorial $latex \vec{A} \times \vec{B}$?
$latex \vec{A} = 2 \hat{i} -3 \hat{j} +4 \hat{k}$
$latex \vec{B} = 1 \hat{i} +5 \hat{j} -2 \hat{k}$
Solução
Como conhecemos os componentes dos vetores, usamos a seguinte fórmula:
$latex C_{x}=A_{y} B_{z} – A_{z} B_{y}$
$latex C_{y}=A_{z} B_{x}-A_{x} B_{z}$
$latex C_{z} =A_{x} B_{y} – A_{y} B_{x}$
onde $latex \vec{C}=\vec{A} \times \vec{B}$. Então:
$latex \vec{A} \times \vec{B} = ((-3)(-2) – (4)(5))\hat{i} +( (4)(1)-(2)(-2))\hat{j} + ((2) (5) – (-3) (1))\hat{k}$
$latex \vec{A} \times \vec{B}=-14\hat{i} + 8\hat{j} + 13\hat{k}$
Veja também
Tem interesse em saber mais sobre vetores? Dê uma olhada nestas páginas:



