Existem duas fórmulas principais que podem ser aplicadas para calcular o produto vetorial de dois vetores. A primeira fórmula usa as magnitudes dos vetores e o ângulo entre suas direções. A segunda fórmula usa os componentes dos vetores.
A seguir, conheceremos as duas fórmulas para calcular o produto vetorial de dois vetores. Em seguida, veremos algumas das propriedades mais importantes do produto vetorial.
FÍSICA
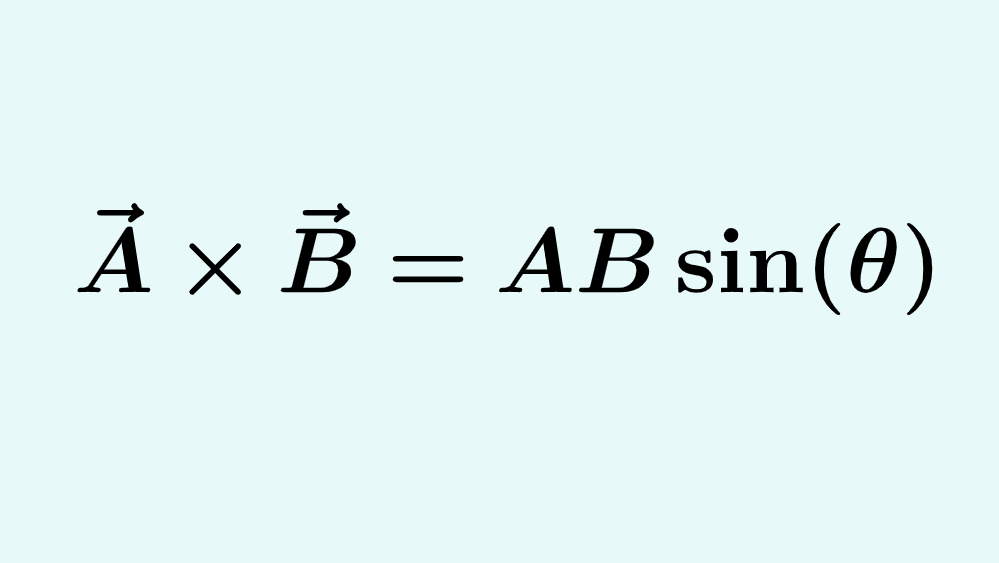
Relevante para…
Aprender sobre as fórmulas e propriedades do produto vetorial de vetores.
FÍSICA
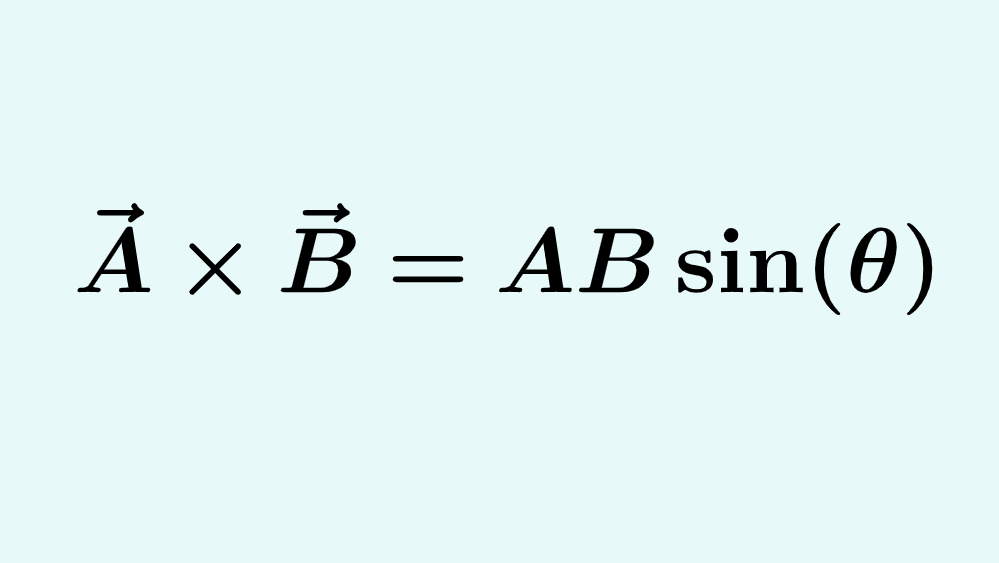
Relevante para…
Aprender sobre as fórmulas e propriedades do produto vetorial de vetores.
Produto vetorial usando magnitudes e ângulos entre vetores
O produto vetorial de dois vetores $latex \vec{A}$ e $latex \vec{B}$ é denotado por $latex \vec{A} \times \vec{B}$. O resultado do produto vetorial é um vetor.
Quando temos as magnitudes dos vetores e o ângulo entre suas direções, a magnitude de seu produto vetorial é calculada com a seguinte fórmula:
$$\vec{A}\times \vec{B}=AB\sin(\theta)$$
onde $latex A$ e $latex B$ são as magnitudes de $latex \vec{A}$ e $latex \vec{B}$ respectivamente, e $latex \theta$ é o ângulo entre os vetores.
Vamos usar o seguinte diagrama para dar uma interpretação geométrica do produto vetorial:
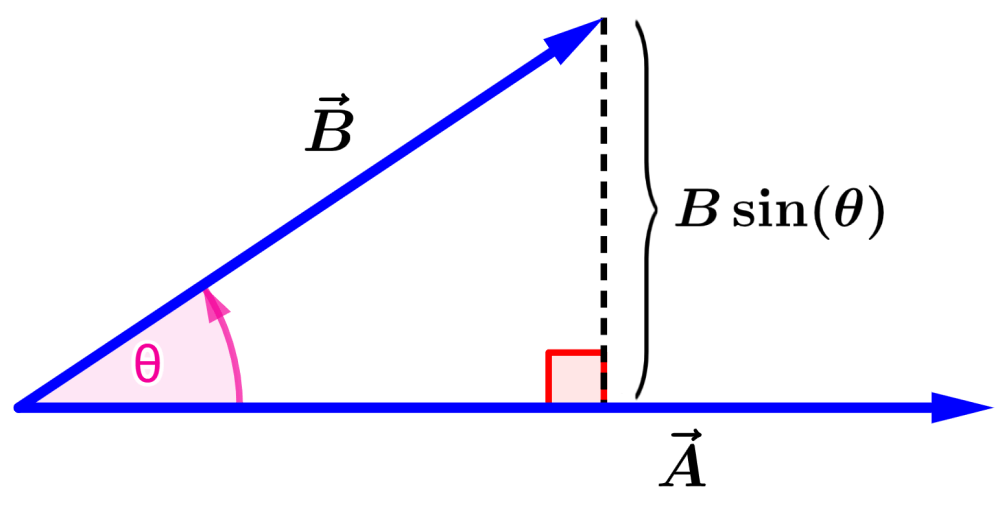
Vemos que $latex B \sin(\theta)$ é a componente de $latex \vec{B}$ que é perpendicular à direção de $latex \vec{A}$.
Alternativamente, a magnitude de $latex \vec{A}\times \vec{B}$ é a magnitude de $latex \vec{B}$ multiplicada pela componente de $latex \vec{A}$ perpendicular à direção de $latex \vec{B}$.
Direção do produto vetorial
O resultado do produto vetorial é um vetor, portanto tem um módulo e uma direção.
A direção do produto vetorial é perpendicular ao plano que contém os vetores $latex \vec{A}$ e $latex \vec{B}$. Ou seja, a direção do produto vetorial é perpendicular a ambos os vetores.
No entanto, sempre existem duas direções perpendiculares a um determinado plano, uma de cada lado do plano. Podemos escolher a direção correta da seguinte maneira:
Usamos nossa mão direita para girar do vetor $latex \vec{A}$ para a direção do vetor $latex \vec{B}$. Nossos dedos devem apontar no sentido de rotação, como mostra a figura:
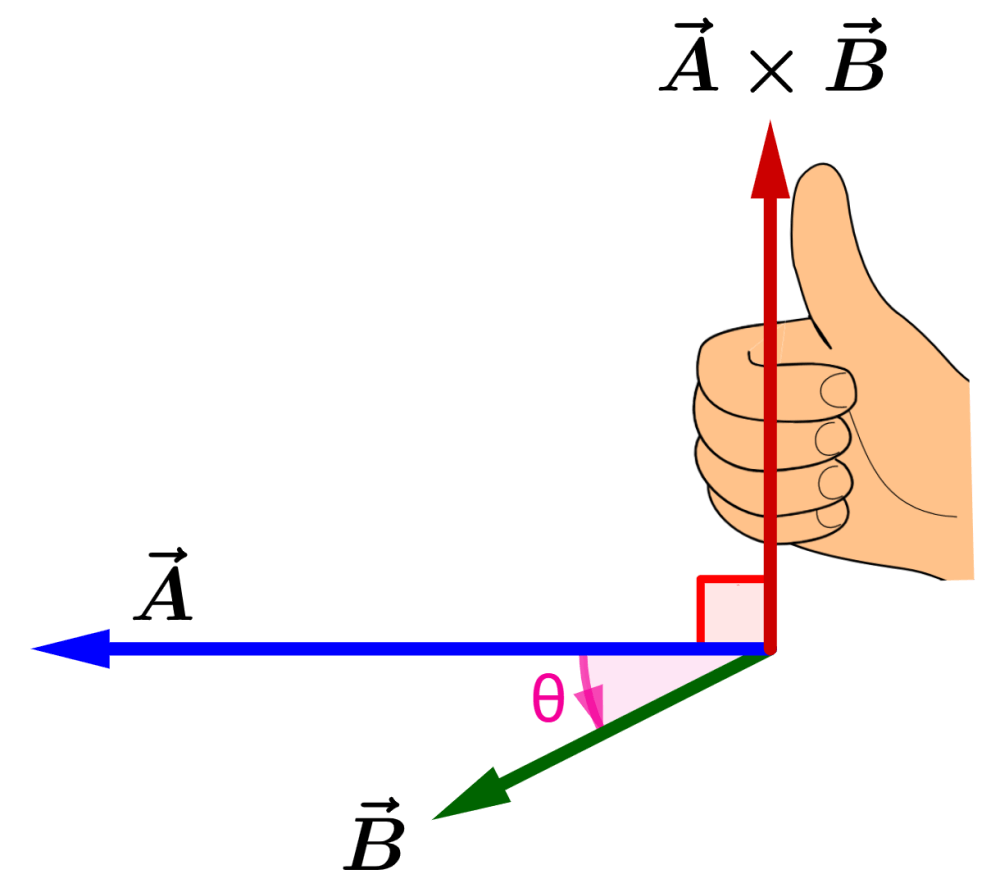
A direção de $latex \vec{A}\times \vec{B}$ corresponde à direção para a qual nosso polegar está apontando.
Da mesma forma, podemos encontrar a direção de $latex \vec{B}\times \vec{A}$ girando do vetor $latex \vec{A}$ para a direção do vetor $latex \vec{B}$, como a imagem mostra:
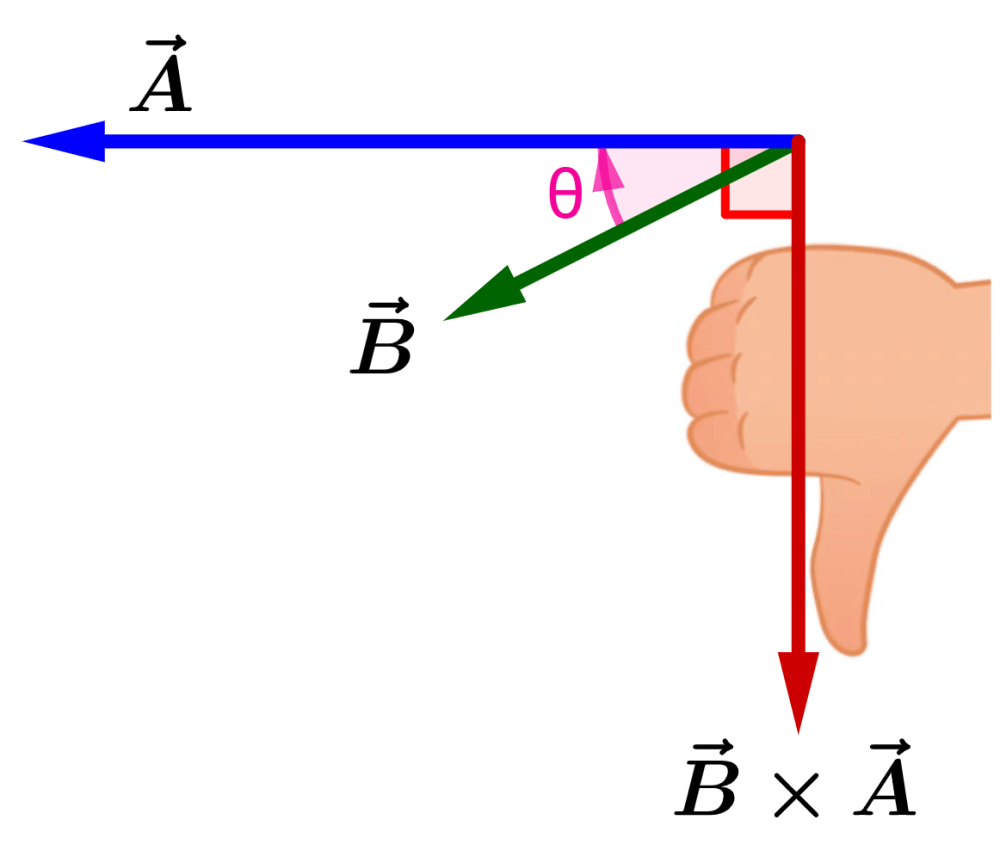
Vemos que $latex \vec{B}\times \vec{A}$ é o oposto de $latex \vec{A}\times \vec{B}$. Ou seja, temos:
$latex \vec{A}\times \vec{B}=-\vec{B}\times \vec{A}$
Produto vetorial de vetores usando seus componentes
Os componentes do produto vetorial de dois vetores $latex \vec{A} \cdot \vec{B}$ podem ser calculadas com a seguinte fórmula se conhecermos os componentes $latex x,~y,~z$ dos vetores:
$latex C_{x}=A_{y}B_{z}-A_{z}B_{y}$
$latex C_{y}=A_{z}B_{x}-A_{x}B_{z}$
$latex C_{z}=A_{x}B_{y}-A_{y}B_{x}$
Para provar esta fórmula, precisamos encontrar o produto vetorial dos vetores unitários $latex \hat{i},~\hat{j},~\hat{k}$.
O produto vetorial de qualquer vetor por si só é 0, então:
$latex \hat{i}\cdot \hat{i}=\hat{j}\cdot \hat{j}=\hat{k}\cdot \hat{k}=0$
Agora, usamos a regra da mão direita para encontrar:
$latex \hat{i}\cdot \hat{j}=-\hat{j}\cdot \hat{i}=\hat{k}$
$latex \hat{j}\cdot \hat{k}=-\hat{k}\cdot \hat{j}=\hat{i}$
$latex \hat{k}\cdot \hat{i}=-\hat{i}\cdot \hat{k}=\hat{j}$
Agora, escrevemos os vetores em termos de suas componentes, expandimos o produto e aplicamos os resultados encontrados acima para simplificar:
$$\vec{A}\times \vec{B}=(A_{x}\hat{i}+A_{y}\hat{j}+A_{z}\hat{k})\times (B_{x}\hat{i}+B_{y}\hat{j}+B_{z}\hat{k})$$
$$=A_{x}\hat{i}\times B_{x}\hat{i}+A_{x}\hat{i}\times B_{y}\hat{j}+A_{x}\hat{i}\times B_{z}\hat{k})$$
$$+A_{y}\hat{j}\times B_{x}\hat{i}+A_{y}\hat{j}\times B_{y}\hat{j}+A_{y}\hat{j}\times B_{z}\hat{k})$$
$$+A_{z}\hat{k}\times B_{x}\hat{i}+A_{z}\hat{k}\times B_{y}\hat{j}+A_{z}\hat{k}\times B_{z}\hat{k})$$
Aqui, podemos reescrever os termos individuais como $latex A_{x}\hat{i}\times B_{y}\hat{j}=A_{x}B_{y}\hat{i}\times\hat{ j}$ e assim por diante. Reagrupando e simplificando, temos:
$latex \vec{A}\times \vec{B}=(A_{y}B_{z}-A_{z}B_{y})\hat{i}+(A_{z}B_{x}-A_{x}B_{z})\hat{j}+(A_{x}B_{y}-A_{y}B_{x})\hat{k}$
Propriedades do produto vetorial de vetores
As propriedades mais importantes do produto vetorial de vetores são as seguintes:
Ortogonalidade
O resultado do produto vetorial é um vetor ortogonal (perpendicular) aos dois vetores de entrada. Se $latex \vec{C}= \vec{A} \times \vec{B}$, então o produto escalar de $latex \vec{C}$ com $latex \vec{A}$ ou $latex \vec {B}$ será zero, ou seja,
$latex \vec{C}\cdot \vec{A} = 0$
e
$latex \vec{C}\cdot \vec{B} = 0$
Não comutatividade
O produto vetorial não é comutativo, o que significa que a ordem dos vetores importa. Para dois vetores $latex \vec{A}$ e $latex \vec{B}$, $latex \vec{A} \times \vec{B}$ não é igual a $latex \vec{B} \times \vec{A}$. De fato,
$latex \vec{A} \times \vec{B} = – \vec{B} \times \vec{A}$
Distributividade
O produto vetorial é distributivo sobre a soma dos vetores. Ou seja, temos
$latex \vec{A} \times (\vec{B} + \vec{C}) = (\vec{A} \times \vec{B}) + (\vec{A} \times \vec{C})$
Multiplicação escalar
O produto vetorial é compatível com a multiplicação escalar. Se $latex \vec{A}$ e $latex \vec{B}$ são vetores e $latex k$ é um escalar, então
$latex k(\vec{A} \times \vec{B}) = (k\vec{A}) \times \vec{B} = \vec{A} \times (k\vec{B})$
Vetores paralelos
Se dois vetores $latex \vec{A}$ e $latex \vec{B}$ são paralelos ou antiparalelos, seu produto vetorial será o vetor nulo (0, 0, 0).
Produto vetorial de um vetor por ele mesmo
Da propriedade anterior, segue-se que o produto de um vetor por ele mesmo é igual a 0:
$latex \vec{A}\times \vec{A}=0$
Regra da mão direita
A direção do produto vetorial pode ser determinada usando a regra da mão direita. Se você apontar o dedo indicador da mão direita na direção do primeiro vetor ($latex \vec{A}$) e o dedo médio na direção do segundo vetor ($latex \vec{B}$), o polegar apontará na direção do produto vetorial ($latex \vec{A} \times \vec{B}$).
Produto escalar triplo
Dados três vetores $latex \vec{A},~ \vec{B}~$ e $latex ~\vec{C}$, o produto escalar triplo é definido como o produto vetorial de $latex \vec{A}$ com o produto escalar de $latex \vec{B}~$ e $latex ~\vec{C}$, ou seja, $latex \vec{A} \times \vec{B} \cdot \vec{C}$.
Esta quantidade é igual ao volume do paralelepípedo formado pelos três vetores com a propriedade de
$latex \vec{A} \times \vec{B} \cdot \vec{C}=\vec{B} \times \vec{C} \cdot \vec{A}=\vec{C} \times \vec{A} \cdot \vec{B}$
Teste de colinearidade
Se $latex \vec{A} \times \vec{B} = 0$ e pelo menos um dos vetores for diferente de zero, então $latex \vec{A}~$ e $latex ~\vec{B}$ Eles são colineares, isto é, eles estão na mesma linha no plano.
Veja também
Interessado em aprender mais sobre vetores? Você pode visitar as páginas a seguir.



