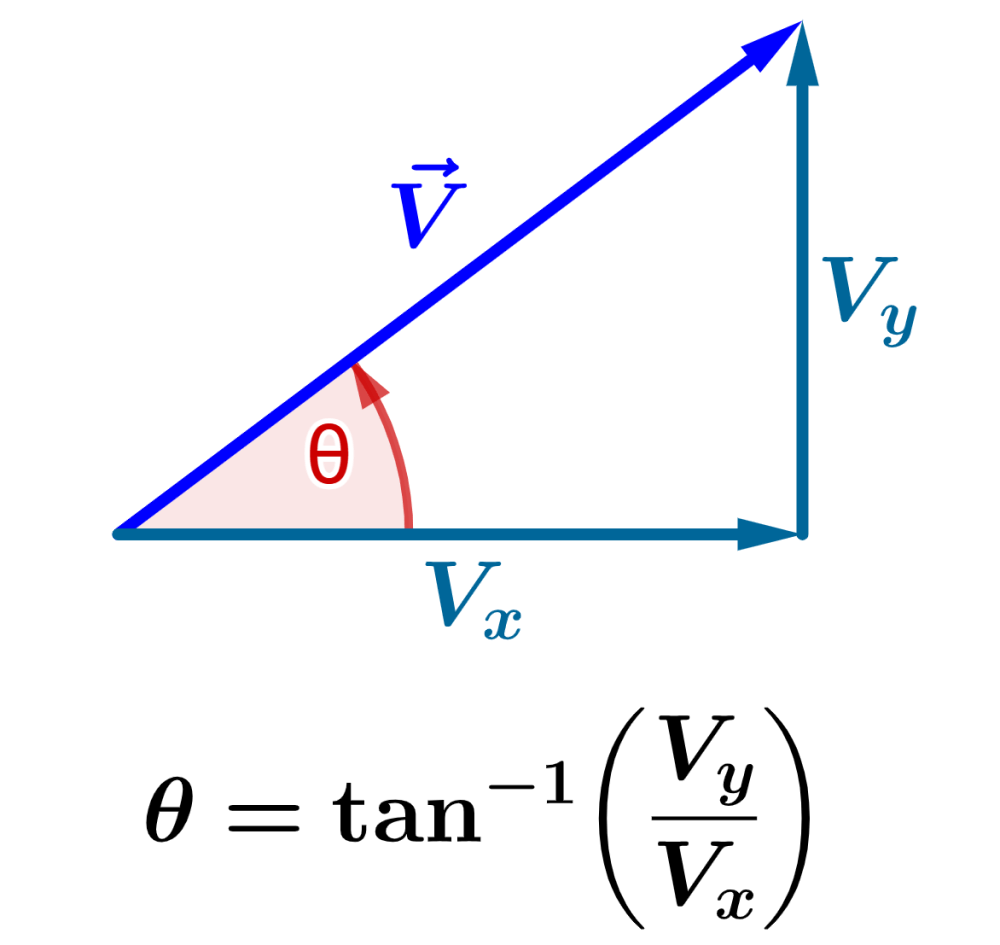A direção de um vetor é a orientação do vetor em um sistema de coordenadas, geralmente descrita pelo ângulo que ele faz com um dos eixos. Para encontrar a direção de um vetor 2D, calculamos a tangente inversa da componente y do vetor sobre o componente x.
Neste artigo, conheceremos a fórmula que podemos aplicar para encontrar a direção de um vetor. Aprenderemos a derivar esta fórmula e a usá-la para resolver alguns exercícios práticos.
Como calcular a direção de um vetor 2D?
Em um sistema de coordenadas cartesianas 2D (plano $latex x, ~y$), a direção de um vetor pode ser especificada pelo ângulo que ele faz com o eixo $latex x$ positivo.
Esse ângulo é normalmente medido no sentido anti-horário, com a faixa de ângulos possíveis de 0° a 360° (0 a 2π radianos).
Para calcular o ângulo de um vetor usando seus componentes, podemos usar trigonometria, especificamente, a função tangente.
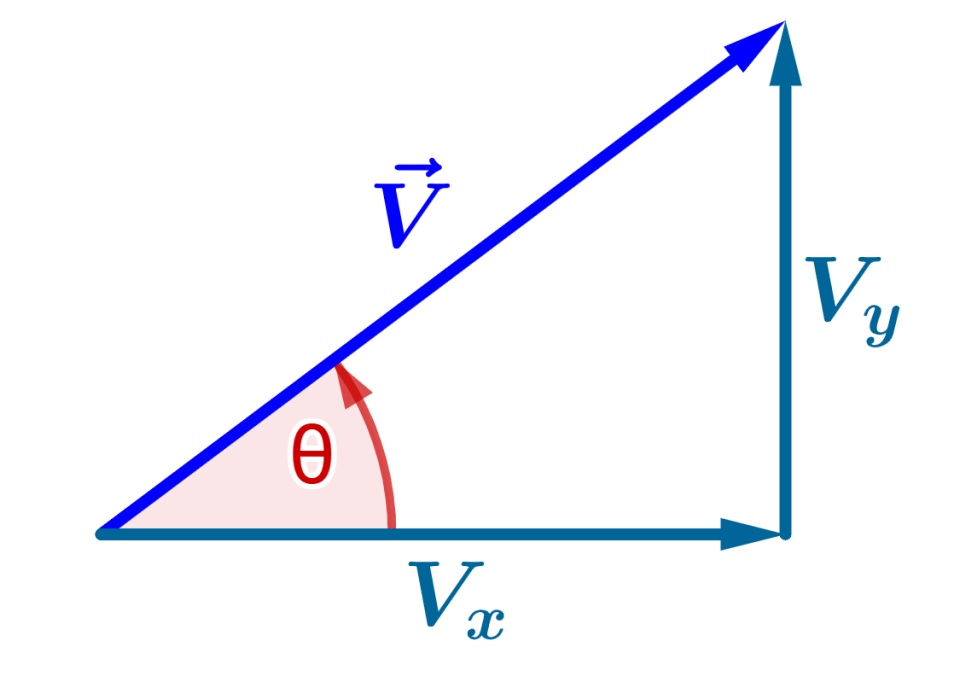
Suponha que temos o vetor $latex \vec{V}$ com os componentes $latex V_{x}$ e $latex V_{y}$ e o ângulo $latex \theta$:
Vemos que temos um triângulo retângulo, onde o vetor $latex \vec{V}$ é a hipotenusa. O lado adjacente (base) é igual a $latex V_{x}$, e o lado oposto (altura) é $latex V_{y}$.
Conforme a definição da função tangente em um triângulo retângulo, temos:
$$\tan(\theta) = \frac{\text{oposto}}{\text{adjacente}}$$
Neste caso,
$$\tan(\theta) = \frac{V_{y}}{V_{x}}$$
Para encontrar θ, temos que pegar a tangente inversa (também chamada de arco tangente ou atan) de ambos os lados da equação. Então,
$$\theta = \tan^{-1}\left(\frac{V_{y}}{ V_{x}}\right)$$
É importante observar em qual quadrante o vetor está, pois a função tangente inversa retorna um resultado entre $latex -\frac{\pi}{2}$ e $latex \frac{\pi}{2 }$ (-90° a 90°).
Então, usamos a tabela a seguir para obter o ângulo correto:
| Quadrante | Valor de $latex \tan^{-1}$ |
| I | Usamos o valor da calculadora |
| II | Adicionamos 180° (π) ao valor da calculadora |
| III | Adicionamos 180° (π) ao valor da calculadora |
| IV | Adicionamos 360° (2π) ao valor da calculadora |
Exercícios resolvidos da direção de um vetor
EXERCÍCIO 1
Encontre o ângulo $latex \theta $ do vetor $latex \vec{A}$ com componentes $latex A_{x} = 3$ e $latex A_{y} = 4$.
Solução
Temos os seguintes componentes:
- $latex A_{x}=3$
- $latex A_{y}=4$
Então, usamos a fórmula para o ângulo ou direção de um vetor:
$$\theta = \tan^{-1}\left(\frac{A_{y}}{ A_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{4}{3}\right)$$
Usando uma calculadora, obtemos:
$latex \theta \approx 53,13^{\circ}$
Portanto, o ângulo do vetor A em relação ao eixo $latex x$ positivo é de aproximadamente 53,13°.
EXERCÍCIO 2
Qual é o ângulo $latex \theta $ do vetor $latex \vec{B}$ com componentes $latex B_{x} = -5$ e $latex B_{y} = 12$?
Solução
Podemos observar as seguintes informações:
- $latex B_{x}=-5$
- $latex B_{y}=12$
Aplicando a fórmula angular com estes componentes, temos:
$$\theta = \tan^{-1}\left(\frac{V_{y}}{ V_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{12}{-5}\right)$$
Utilizando uma calculadora, obtemos:
$latex \theta \approx -67,38^{\circ}$
Porém, como o vetor está no segundo quadrante ($latex x$ negativo, $latex y$ positivo), devemos somar 180° ao resultado:
$latex \theta = -67,38^{\circ} + 180^{\circ} $
$latex \theta = 112,62^{\circ}$
Portanto, o ângulo do vetor B em relação ao eixo $latex x$ positivo é de aproximadamente 112,62°.
EXERCÍCIO 3
Calcula o ângulo $latex \theta $ do vetor $latex \vec{C}$ com as componentes $latex C_{x} = -6$ e $latex C_{y} = -8$.
Solução
Podemos obter as seguintes informações:
- $latex C_{x}=-6$
- $latex C_{y}=-8$
Substituindo estes valores pela fórmula para o ângulo de um vector, temos:
$$\theta = \tan^{-1}\left(\frac{C_{y}}{ C_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{-8}{-6}\right)$$
Usando uma calculadora, obtemos:
$latex \theta \approx 53,13^{\circ}$
Como o vetor está no terceiro quadrante ($latex x$ negativo, $latex y$ negativo), devemos somar 180° ao resultado:
$latex \theta = 53,13^{\circ} + 180^{\circ} $
$latex \theta = 233,13^{\circ}$
EXERCÍCIO 4
Qual é o ângulo $latex \theta $ do vetor $latex \vec{D}$ com componentes $latex D_{x} = 7$ e $latex D_{y} = -3$?
Solução
Podemos extrair as seguintes informações:
- $latex D_{x}=7$
- $latex D_{y}=-3$
O ângulo do vector é igual a:
$$\theta = \tan^{-1}\left(\frac{D_{y}}{ D_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{-3}{7}\right)$$
Utilizando uma calculadora, obtemos:
$latex \theta \approx -23,2^{\circ}$
Como o vetor está no quarto quadrante ($latex x$ positivo, $latex y$ negativo), podemos somar 360° ao resultado:
$latex \theta = -23,2^{\circ} + 360^{\circ}$
$latex \theta = 336,8^{\circ}$
EXERCÍCIO 5
Se um vetor tem as componentes $latex A_{x} = -10$ e $latex A_{y} = 0$, qual é o seu ângulo $latex \theta$?
Solução
Neste caso, temos um componente $latex y$ igual a zero, então usando a função tangente inversa, obteremos um ângulo igual a zero.
Podemos resolver este problema considerando o componente $latex x$ negativo. Então, sabemos que o ângulo formado deve ser igual a 180°.
$latex \theta =180^{\circ}$
Quando temos problemas semelhantes a este, é útil considerar a posição nos eixos do plano cartesiano.
EXERCÍCIO 6
Encontre o ângulo $latex \theta $ do vetor $latex \vec{G}$ com os componentes $latex G_{x} = 8$ e $latex G_{y} = 15$.
Solução
Temos os seguintes componentes:
- $latex G_{x}=8$
- $latex G_{y}=15$
Depois, utilizamos a fórmula para o ângulo ou direcção de um vector:
$$\theta = \tan^{-1}\left(\frac{G_{y}}{ G_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{15}{8}\right)$$
Utilizando uma calculadora, obtemos:
$latex \theta \approx 61,93^{\circ}$
EXERCÍCIO 7
Qual é o ângulo $latex \theta $ do vetor $latex \vec{H}$ com componentes $latex H_{x} = -12$ e $latex H_{y} = -5$?
Solução
Podemos observar o seguinte:
- $latex H_{x}=-12$
- $latex H_{y}=-5$
Aplicando a fórmula do ângulo de um vetor 2D, temos:
$$\theta = \tan^{-1}\left(\frac{H_{y}}{ H_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{-5}{-12}\right)$$
Usando uma calculadora, obtemos:
$latex \theta \approx 22,62^{\circ}$
Como o vetor está no terceiro quadrante ($latex x$ negativo, $latex y$ negativo), devemos somar 180° ao resultado:
$latex \theta = 22,62^{\circ} + 180^{\circ}$
$latex \theta = 202,62^{\circ}$
EXERCÍCIO 8
Um avião está voando para o norte a uma velocidade de 150 km/h. Há um forte vento de oeste que empurra o avião para leste com uma velocidade de 40 km/h. Qual é a direção do avião em relação ao solo?
Solução
Vamos representar a velocidade do avião com $latex \vec{A}$ e a velocidade do vento com $latex \vec{V}$.
Como o avião está voando para o norte, seus componentes de velocidade são $latex A_{x} = 0$ km/h e $latex A_{y} = 150$ km/h. O vento é do oeste, então seus componentes de velocidade são $latex V_{x} = 40$ km/h e $latex V_{y} = 0$ km/h.
Para encontrar a velocidade real e a direção do avião em relação ao solo, $latex \vec{R}$, temos que somar as componentes da velocidade do avião e as componentes da velocidade do vento:
$latex R_{x} = A_{x} + V_{x} = 0 + 40 = 40$ km/h
$latex R_{y} = R_{y} + V_{y} = 150 + 0 = 150$ km/h
Agora, usamos a fórmula do ângulo com esses componentes:
$$\theta = \tan^{-1}\left(\frac{R_{y}}{ R_{x}}\right)$$
$$\theta = \tan^{-1}\left(\frac{150}{40}\right)$$
$latex \theta \approx 75,62^{\circ}$
Como o ângulo é medido a partir do eixo $latex x$ positivo (leste), o avião está voando aproximadamente 75,62° ao norte do leste.
Direção de vetores 2D – Exercícios para resolver
Encontre o ângulo θ de um vetor com os componentes $latex V_{x}=0$ e $latex V_{y}=-14$.
Escreva o ângulo em graus.
Veja também
Interessado em aprender mais sobre vetores? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
