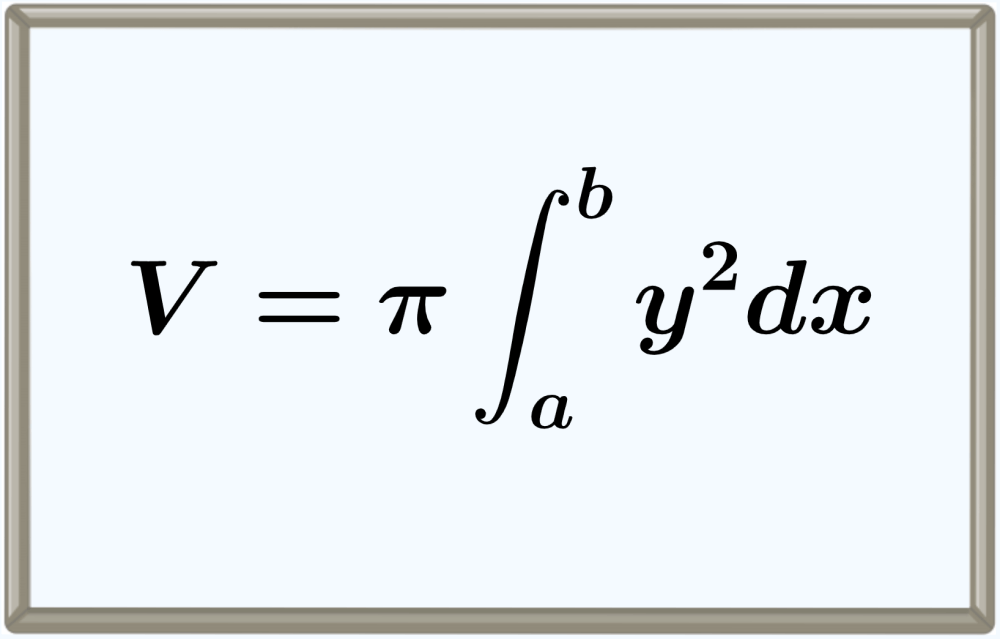O volume de revolução em torno do eixo x pode ser encontrado avaliando uma integral definida em relação ao quadrado da equação da curva e multiplicando o resultado por π. Podemos derivar uma fórmula para calcular este volume utilizando limites e integrais.
Neste artigo, aprenderemos como calcular o volume de revolução em relação ao eixo x. Aprenderemos a derivar a sua fórmula e a utilizá-la em alguns exemplos práticos.
CÁLCULO
Relevante para…
Aprender a calcular o volume de revolução em torno do eixo x.
CÁLCULO
Relevante para…
Aprender a calcular o volume de revolução em torno do eixo x.
Como encontrar o volume de revolução em torno do eixo x
Para encontrar o volume de revolução de um sólido em relação ao eixo x, podemos aplicar a seguinte fórmula:
$$V=\pi \int_{a}^{b} y^2 d x$$
Depois, podemos seguir o seguinte processo para utilizar corretamente a fórmula:
1. Encontrar o quadrado da equação da curva que forma o volume de revolução.
Ou seja, começamos por encontrar $latex y^2$.
2. Encontrar o valor da integral definida $latex \int_{a}^{b} y^2 d x$.
Para isto, substituímos a expressão por $latex y^2$ do passo 1.
3. Multiplique o resultado do passo 2 por π para encontrar o volume do sólido formado.
Se precisar de rever como resolver integrais definidas, pode visitar o nosso artigo: Como calcular integrais definidas.
Prova da fórmula para o volume de revolução em torno do eixo x
Para encontrar uma fórmula para o volume de revolução com o eixo x, começamos por considerar a área sob a curva $latex y=x^2$ de $latex x=1$ até $latex x=2$, como mostra o diagrama:
Agora, considere o sólido formado quando esta área é girada 2π em torno do eixo x, como mostra o diagrama abaixo. Podemos calcular o seu volume utilizando o cálculo integral.
Pegamos numa faixa muito pequena de comprimento $latex x$ sob a curva $latex f(x)$, como mostra o diagrama abaixo:
Quando esta pequena área é girada em 2π radianos em torno do eixo x, formamos um disco com um raio igual a $latex y$ e uma largura de $latex \delta x$. O volume deste disco é:
$latex \delta V= \pi y^2 \delta x$
Para encontrar o volume de todo o sólido, temos de encontrar a soma de todos os discos de $latex x=a$ até $latex x=b$. Então, temos:
$$V=\sum_{x=a}^{b}\pi y^2 \delta x$$
Como $latex \delta \to 0$, esta soma se aproxima do valor de $latex V$, então temos:
$$V=\lim_{\delta x \to 0} \pi \sum_{x=a}^{b} y^2 \delta x$$
que é igual a
$$V=\pi \int_{a}^{b} y^2 d x$$
Exercícios resolvidos do volume de revolução em torno do eixo x
EXERCÍCIO 1
Encontrar o volume gerado quando a área abaixo de $latex y=x$ de $latex x=0$ até $latex x=6$ é rodada em relação ao eixo x.
Solução
Começamos por escrever a fórmula para o volume de revolução:
$$V=\pi \int_{a}^{b} y^2 d x$$
Agora, substituímos a expressão por $latex y $ e resolvemos a integral definida:
$$V=\pi \int_{0}^{6} x^2 d x$$
$$=\pi \left[ \frac{x^3}{3} \right]_{0}^{6}$$
$$=\pi \left( \frac{216}{3} \right)-(0)$$
$latex V=72 \pi $
EXERCÍCIO 2
Qual é o volume gerado quando a área abaixo de $latex y=x^2$ de $latex x=0$ até $latex x=5$ é rodada em relação ao eixo x?
Solução
A fórmula para o volume de revolução em torno do eixo x é:
$$V=\pi \int_{a}^{b} y^2 d x$$
Neste caso, temos $latex y=x^2$, pelo que substituímos na fórmula e avaliamos a integral definida:
$$V=\pi \int_{0}^{5} x^4 d x$$
$$=\pi \left[ \frac{x^5}{5} \right]_{0}^{5}$$
$$=\pi \left( \frac{3125}{5} \right)-(0)$$
$latex V=625 \pi $
EXERCÍCIO 3
Encontrar o volume do sólido formado quando a área abaixo de $latex y=x^2+2$ de $latex x=1$ até $latex x=3$ é rodada em relação ao eixo x.
Solução
O volume do sólido é dado pela seguinte fórmula:
$$V=\pi \int_{a}^{b} y^2 d x$$
Ao quadrar $latex y$, temos $latex y^2=(x^2+2)^2$, que é igual a $latex y^2=x^4+4x^2+4$. Então, temos:
$$V=\pi \int_{1}^{3} (x^4+4x^2+4) d x$$
$$=\pi \left[ \frac{x^5}{5} + \frac{4x^3}{3}+4x \right]_{1}^{3}$$
$$=\pi \left( \frac{483}{5}- \frac{83}{15} \right)$$
$$ V=\frac{1366 \pi}{15} $$
EXERCÍCIO 4
Encontre o volume de revolução da área sob $latex y=3\sqrt{x}$ de $latex x=2$ até $latex x=4$ em relação ao eixo x.
Solução
Começamos com a seguinte fórmula para encontrar o volume:
$$V=\pi \int_{a}^{b} y^2 d x$$
Quando temos $latex y $ ao quadrado, obtemos $latex y^2=9x$. Depois, utilizamos isto na fórmula para resolver a integral definida:
$$V=\pi \int_{2}^{4} 9x d x$$
$$=\pi \left[ \frac{9x^2}{2} \right]_{2}^{4}$$
$latex =\pi (72 )-( 18)$
$latex V=54\pi $
EXERCÍCIO 5
Encontre o volume de revolução quando a área sob $latex y=\sqrt{x^2+3x}$ de $latex x=2$ eté $latex x=6$ é girada no eixo x.
Solução
Começamos por escrever a fórmula para o volume de revolução com o eixo x:
$$V=\pi \int_{a}^{b} y^2 d x$$
Quando elevamos ao quadrado $latex y $, temos $latex y^2=(\sqrt{x^2+3x})^2$, que é igual a $latex y^2=x^2+3x$. Então temos:
$$V=\pi \int_{2}^{6} (x^2+3x) d x$$
$$=\pi \left[ \frac{x^3}{3} + \frac{3x^2}{2} \right]_{2}^{6}$$
$$=\pi [72 + 54 ]-\left[ \frac{8}{3} + 6 \right]$$
$$=\pi \left( \frac{352}{3} \right)$$
$$ V=\frac{352\pi}{3} $$
EXERCÍCIO 6
A área delimitada entre a curva $latex y=4-x^2$ e a recta $latex y=4-2x$ é rodada em relação ao eixo x. Encontrar o volume do sólido gerado.
Solução
Neste caso, temos uma área entre duas curvas. Depois, podemos desenhar um gráfico simples para visualizar essa área:
Agora, vemos que a área a ser rodada é uma área entre duas curvas. Por isso, resolvemos da seguinte forma:
$$V=\pi \int_{0}^{2} (4-x^2)^2 d x-\pi \int_{0}^{2} (4-2x)^2 d x$$
$$=\pi \int_{0}^{2} (4-x^2)^2 – (4-2x)^2 d x$$
$$=\pi \int_{0}^{2} (x^4-12x^2+16x) d x$$
$$=\pi \left[ \frac{x^5}{5}-4x^3+8x^2 \right]_{0}^{2}$$
$$=\pi \left[ \frac{32}{5}-32+32 \right]-[0]$$
$latex V=\frac{32\pi}{5} $
Volume de revolução em torno do eixo x – Exercícios para resolver
Qual é o volume de revolução da área sob $latex y=\sqrt{3x^2+8}$ de $latex x=1$ até $latex x=3$ em relação ao eixo x?
Escreva a resposta na caixa.
Veja também
Interessado em aprender mais sobre integrais de funções? Você pode olhar para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
