A área sob uma curva pode ser encontrada usando integrais definidas. Por sua vez, as integrais definidas são calculadas integrando a função e avaliando tanto o limite inferior quanto o limite superior. O limite inferior é subtraído do limite superior para obter um determinado valor para a área.
A seguir, veremos alguns exercícios resolvidos da área sob uma curva. Além disso, veremos alguns exercícios práticos para aplicar o que foi aprendido.
Processo usado para encontrar a área sob uma curva
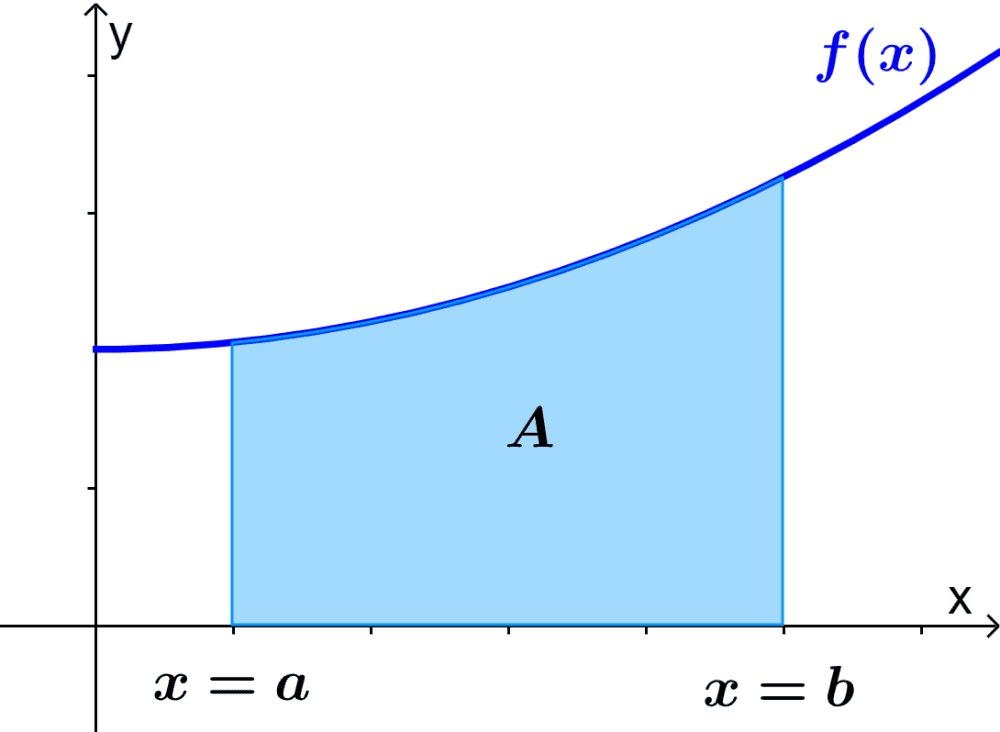
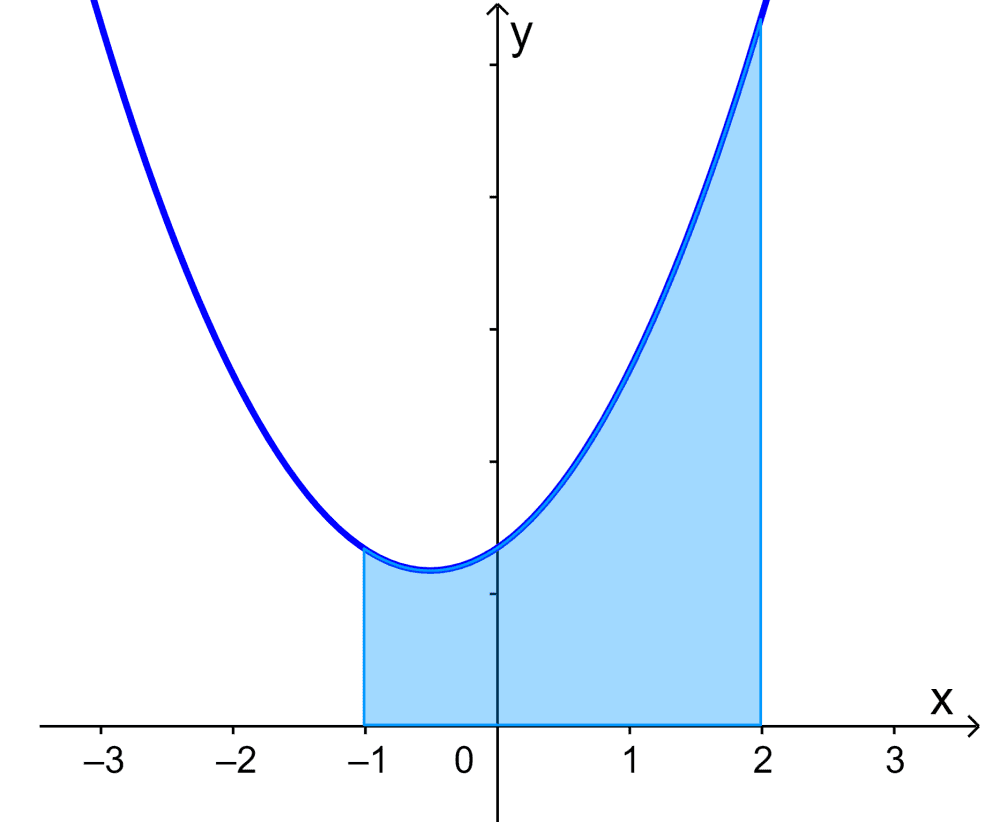
Consideramos a área $latex A$ sob a curva $latex f(x)$ mostrada no diagrama a seguir:
Podemos encontrar a área sob esta curva usando uma integral definida. Neste caso, a área sob a curva é representada por $latex A= \int_{a}^{b} f(x)dx$, onde,
- $latex dx$ indica que os limites $latex a $ e $latex b$ são limites de x.
- A constante $latex a$ é o limite inferior da integral.
- A constante $latex b$ é o limite superior da integral.
Levando isso em consideração, podemos seguir os passos abaixo para encontrar a área sob uma curva supondo que queremos encontrar a área sob $latex 2x$ entre $latex x=0$ e $latex x=1$.
Passo 1: Forme uma integral definida com as informações fornecidas. Neste caso, temos a seguinte integral:
$latex \int_{0}^{1} 2xdx$
Passo 2: Obtenha a integral da função e expresse-a usando colchetes, onde escrevemos os limites de integração da seguinte forma:
$latex \int_{0}^{1} 2xdx=[x^2+c]_{0}^{1}$
Passo 3: Avaliamos os limites superior e inferior da expressão integrada. Subtraímos o limite inferior do limite superior:
$latex [x^2+c]_{0}^{1}=[(1)^2+c]-[(0)^2+c]$
Passo 4: Simplifique para um único valor numérico:
$latex =[(1)^2+c]-[(0)^2+c]$
$latex =[1+c]-[0+c]$
$latex =1$
O valor encontrado corresponde à área.
Ao resolver integrais definidas, as constantes de integração são geralmente ignoradas, pois serão canceladas no passo 3 de qualquer maneira.
Exercícios resolvidos da área sob uma curva
EXERCÍCIO 1
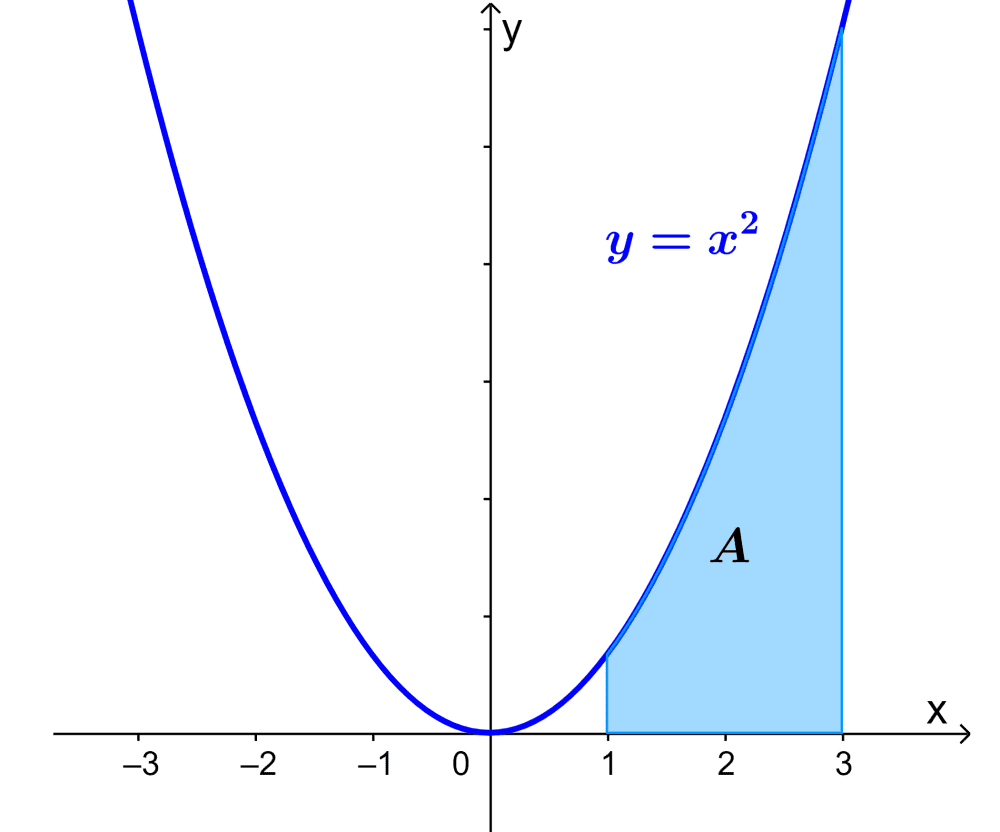
Qual é a área sob a curva representada por $latex y=x^2$ entre $latex x=1$ e $latex x=3$?
Solução
Para resolver este exercício, temos que começar formando uma integral definida com as informações fornecidas. Então temos:
$$A=\int_{1}^{3} x^2 dx$$
Agora, encontramos a integral da expressão e mantemos os limites de integração usando colchetes:
$$A=\left[ \frac{x^3}{3} \right]_{1}^{3}$$
Quando avaliamos os limites de integração, temos:
$$A=\left[ \frac{(3)^3}{3} \right]-\left[ \frac{(1)^3}{3} \right]$$
Por fim, podemos simplificar:
$$A=\left[ \frac{27}{3} \right]-\left[ \frac{1}{3} \right]$$
$$A=[9]-\left[ \frac{1}{3} \right]$$
$$A= \frac{26}{3}$$
EXERCÍCIO 2
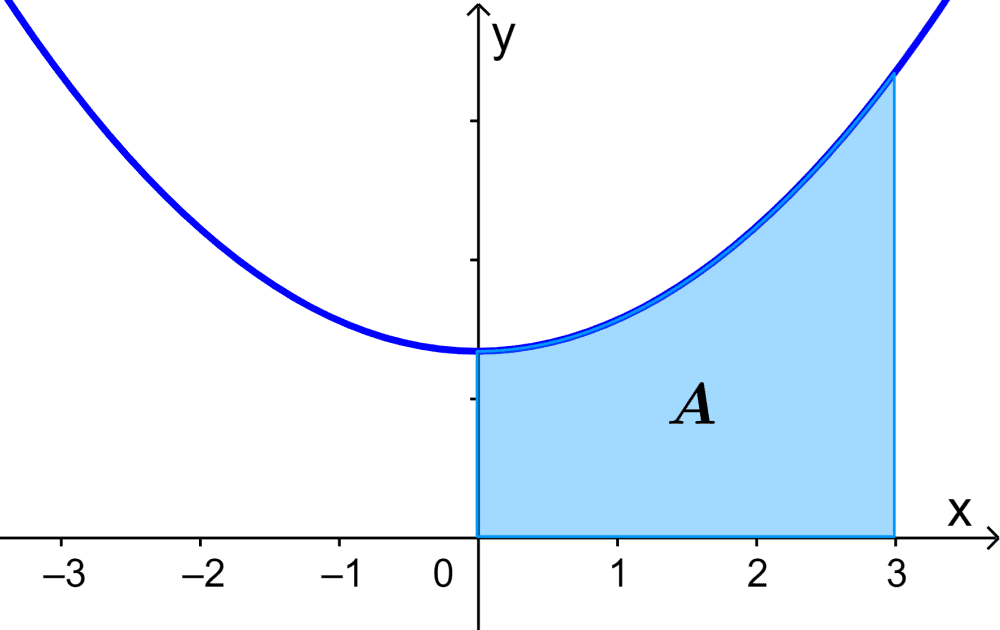
Determine a área sob a curva representada por $latex y=\frac{1}{3}x^2+2$ já que $latex x=0$ e $latex x=3$.
Solução
Com as informações dadas, podemos formar a seguinte integral definida:
$$A=\int_{0}^{3} \frac{1}{3} x^2+2 dx$$
Agora, integramos à expressão dada e mantemos os limites de integração:
$$A=\left[ \frac{1}{9} x^3+2x \right]_{0}^{3}$$
Quando avaliamos os limites de integração na expressão integrada, temos:
$$A=\left[\frac{1}{9}(3)^3+2(3) \right]-\left[\frac{1}{9}(0)^3+2(0) \right]$$
Simplificando, temos:
$$A=[3+6]-[0]$$
$$A=9$$
EXERCÍCIO 3
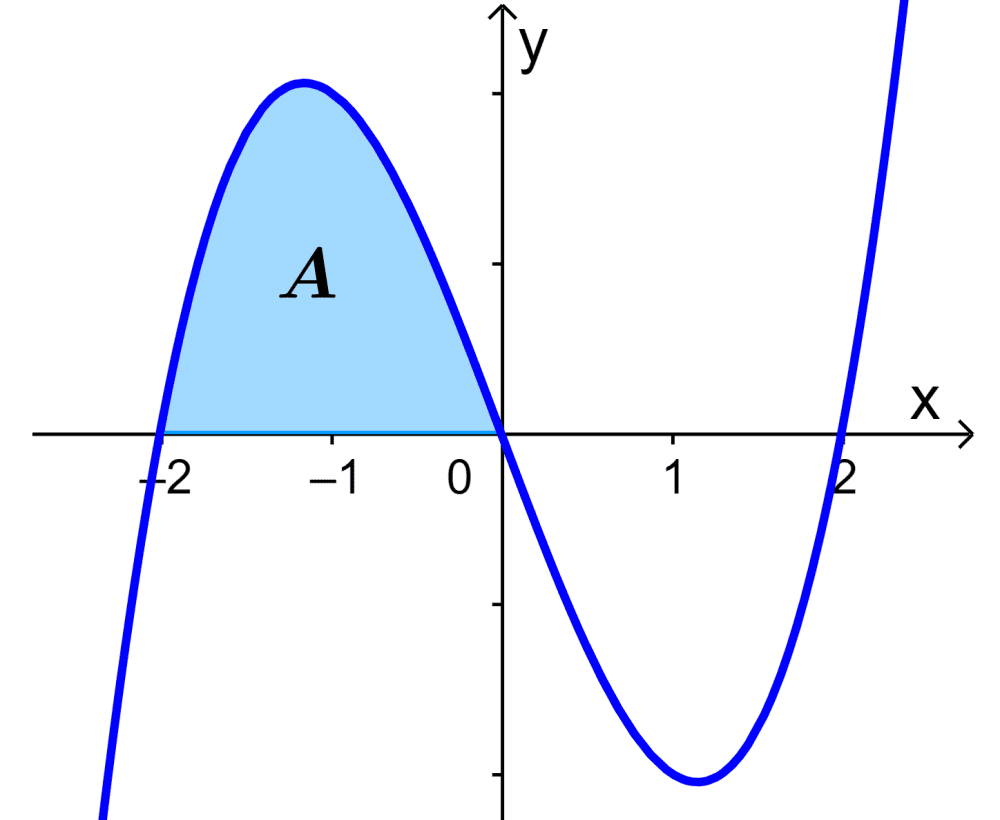
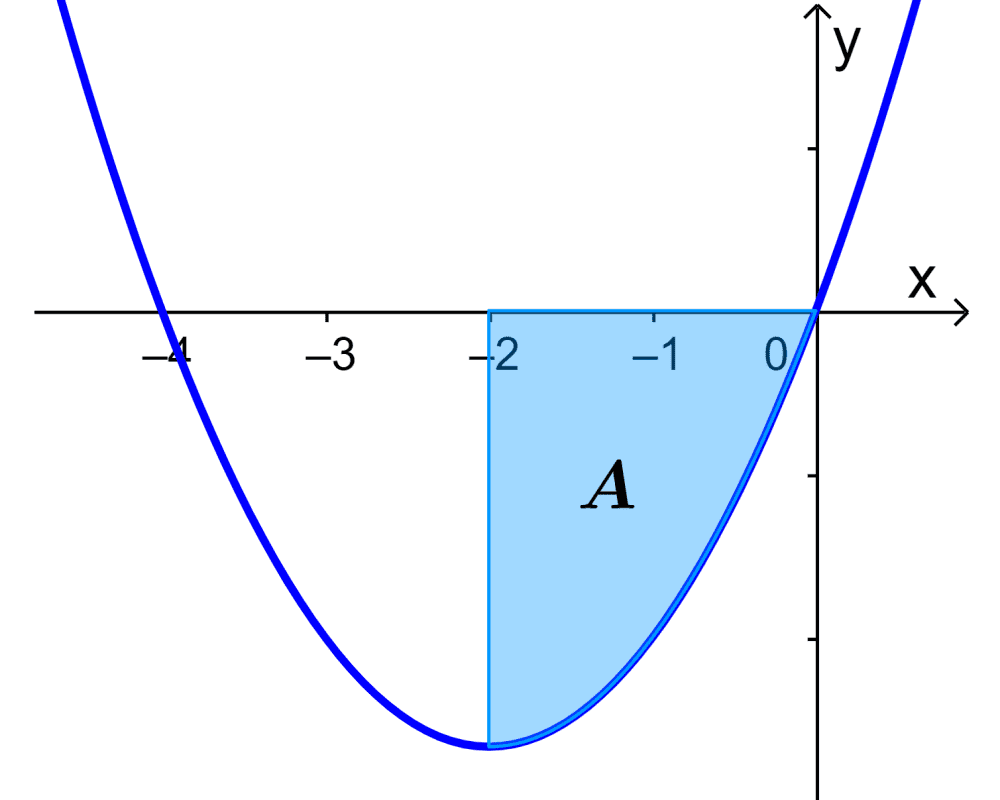
Qual é a área da curva representada por $latex y=x^3-4x$ de $latex x=-2$ até $latex x=0$?
Solução
Começamos formando uma integral definida com as informações fornecidas:
$$A=\int_{-2}^{0} x^3-4x dx$$
Agora, integramos a expressão e mantemos os limites de integração:
$$A=\left[ \frac{x^4}{4} -2x^2 \right]_{-2}^{0}$$
Quando avaliamos os limites de integração, temos:
$$A=\left[ \frac{(0)^4}{4} -2(0)^2 \right]-\left[ \frac{(-2)^4}{4} -2(-2)^2 \right]$$
Simplificamos para obter um único valor para a área:
$$A=[ 0 -0]-\left[ \frac{16}{4} -2(4) \right]$$
$latex A=-[ 4-8]$
$latex A= 4$
EXERCÍCIO 4
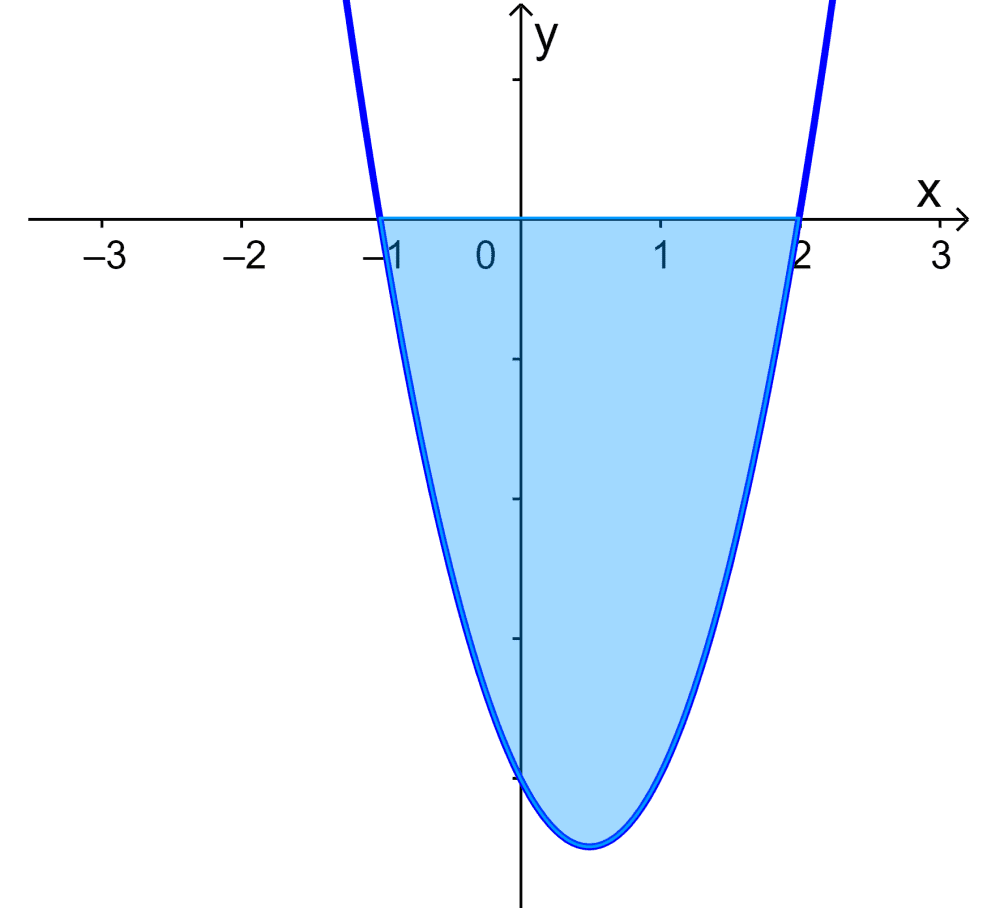
Encontre a área sob a curva $latex y=x^2+x+2$ de $latex x=-1$ até $latex x=2$.
Solução
Formando uma integral com a informação dada, temos:
$$A=\int_{-1}^{2} x^2+x+2 dx$$
Agora, podemos integrar a expressão mantendo os limites de integração:
$$A=\left[ \frac{x^3}{3} +\frac{x^2}{2}+2x \right]_{-1}^{2}$$
Avaliando isso, temos:
$$A=\left[ \frac{(2)^3}{3} +\frac{(2)^2}{2}+2(2) \right]-\left[ \frac{(-1)^3}{3} +\frac{(-1)^2}{2}+2(-1) \right]$$
Quando simplificamos, temos:
$$A=\left[ \frac{8}{3} +2+4 \right]-\left[ -\frac{1}{3} +\frac{1}{2}-2 \right]$$
$$A=\left[ \frac{26}{3}\right]-\left[ -\frac{11}{6} \right]$$
$latex A=\frac{63}{6}$
$latex A= 10~\frac{1}{2}$
EXERCÍCIO 5
Se tivermos uma curva representada por $latex y=x^2+4x$, encontre a área da região de $latex x=-2$ até $latex x=0$.
Solução
Neste caso, a região que queremos está abaixo do eixo x. No entanto, podemos seguir o mesmo processo e encontrar uma integral definida com as informações fornecidas:
$$A=\int_{-2}^{0} x^2 +4x dx$$
Determinando a integral da expressão e mantendo os limites de integração, temos:
$$A=\left[ \frac{x^3}{3} +2x^2 \right]_{-2}^{0}$$
Avaliando os limites de integração, temos:
$$A=\left[ \frac{(0)^3}{3} +2(0)^2 \right]-\left[ \frac{(-2)^3}{3} +2(-2)^2 \right]$$
Quando simplificamos, obtemos o seguinte:
$$A=[ 0 +0]-\left[ \frac{-8}{3} +8 \right]$$
$$A=-\left[ \frac{16}{3} \right]$$
Vemos que obtivemos um valor negativo. A razão para isso é que a área que queremos está sob o eixo x. Então, ignoramos o sinal de menos e a área é igual a $latex A= \frac{16}{3} $.
Neste exercício, podemos entender por que é útil desenhar um gráfico simples quando queremos encontrar a área sob uma curva.
EXERCÍCIO 6
Encontre a área sob a curva $latex y=3x^2-3x-6$ de $latex x=-1$ até $latex x=2$.
Solução
Este exercício é semelhante ao anterior. Portanto, devemos usar o mesmo processo e ignorar o sinal negativo resultante.
Formando a integral definida, temos:
$$A=\int_{-1}^{2} 3x^2-3x-6 dx$$
Determinando a integral da expressão e mantendo os limites de integração, temos:
$$A=\left[ x^3 -\frac{3x^2}{2}-6x \right]_{-1}^{2}$$
Quando avaliamos os limites de integração, temos:
$$A=\left[ (2)^3 -\frac{3(2)^2}{2}-6(2) \right]-\left[ (-1)^3 -\frac{3(-1)^2}{2}-6(-1) \right]$$
Simplificando, temos:
$$A=[ 8 -6-12 ]-\left[ -1 -\frac{3}{2}+6 \right]$$
$$A=[ -10 ]-\left[ \frac{7}{2} \right]$$
$$A=-\frac{27}{2}=-13,5$$
A área é igual a $latex A= 13,5 $.
EXERCÍCIO 7
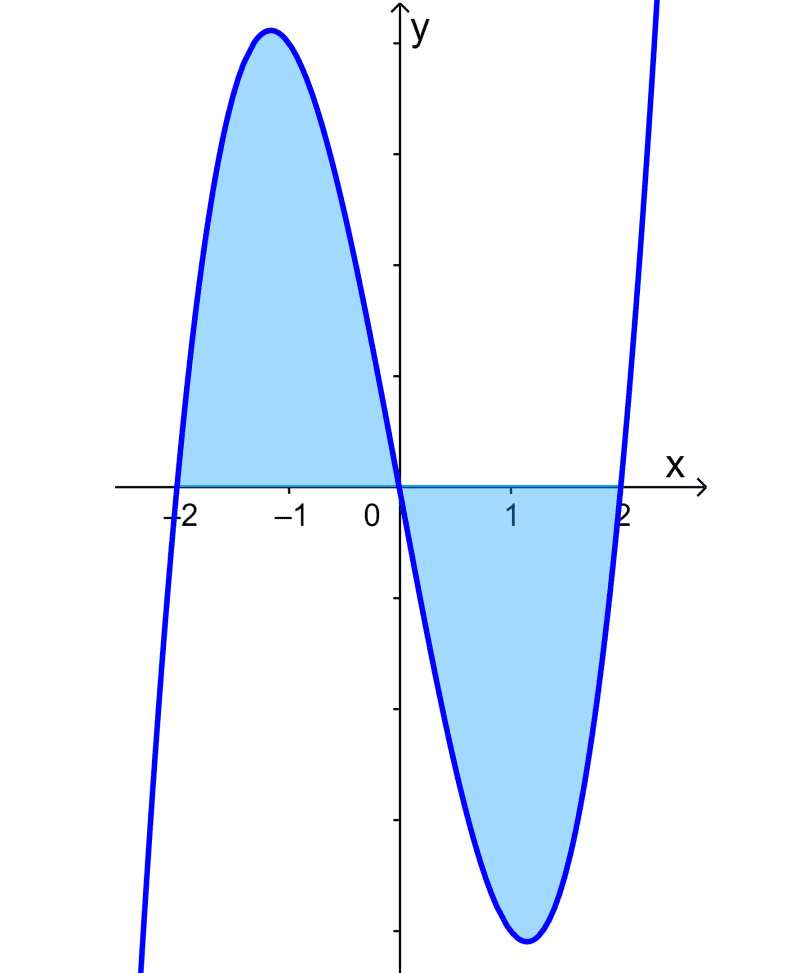
Encontre a área sob a curva $latex y=2x^3-8x$ de $latex x=-2$ até $latex x=2$.
Solução
Podemos resolver isso encontrando as áreas abaixo do eixo x e acima do eixo x separadamente. No entanto, neste caso, vemos que o gráfico é simétrico e ambas as regiões possuem a mesma área.
Portanto, podemos encontrar a área de uma região e depois multiplicá-la por 2. Então, começamos formando a seguinte integral definida:
$$A=\int_{-2}^{0} 2x^3-8x dx$$
Agora, escrevemos da seguinte forma:
$$A=\left[ \frac{x^4}{2}-4x^2 \right]_{-2}^{0}$$
Avaliando isso, temos:
$$A=\left[ \frac{(0)^4}{2}-4(0)^2 \right]-\left[ \frac{(-2)^4}{2}-4(-2)^2 \right]$$
Finalmente, simplificamos para obter um único valor:
$latex A=[0-0]-[ 8 -16]$
$latex A= 8$
Portanto, a área da região de $latex x=-2$ a $latex x=2$ é 16.
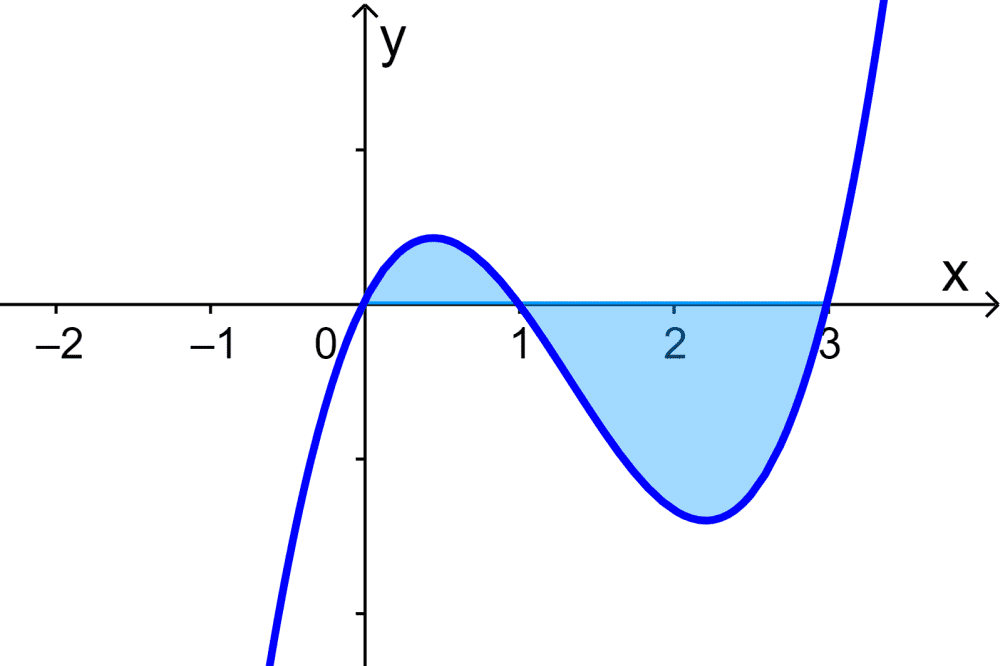
EXERCÍCIO 8
Se tivermos a curva $latex y=x^3-4x^2+3x$, qual é a área sob a curva de $latex x=0$ até $latex x=3$?
Solução
Nesse caso, a área necessária tem duas partes, $latex A_{1}$, a área acima do eixo x, e $latex A_{2}$, a área abaixo do eixo x. Então, vamos encontrar essas áreas separadamente.
Para a área $latex A_{1}$, temos a seguinte integral definida:
$$A_{1}=\int_{0}^{1} (x^3-4x^2+3x) dx$$
Podemos resolver essa integral da seguinte forma:
$$A_{1}=\left[ \frac{x^4}{4}-\frac{4x^3}{3}+\frac{3x^2}{2} \right]_{0}^{1}$$
$$A_{1}=\left[ \frac{1}{4}-\frac{4}{3}+\frac{3}{2} \right]-[ 0]$$
$$A_{1}=\frac{5}{12}$$
Para a área $latex A_{2}$, temos a seguinte integral definida:
$$A_{2}=\int_{1}^{3} (x^3-4x^2+3x) dx$$
E resolvemos da seguinte forma:
$$A_{2}=\left[ \frac{x^4}{4}-\frac{4x^3}{3}+\frac{3x^2}{2} \right]_{1}^{3}$$
$$A_{2}=\left[ \frac{81}{4}-36+\frac{27}{2} \right]-\left[ \frac{1}{4}-\frac{4}{3}+\frac{3}{2} \right]$$
$$A_{2}=-\frac{9}{4}-\frac{5}{12}$$
$$A_{2}=-\frac{8}{3}$$
Finalmente, calculamos a área total $latex A$ da seguinte forma:
$$A=A_{1}+A_{2}$$
$$A=\frac{5}{12}+\frac{8}{3}$$
$$A=\frac{37}{12}$$
Exercícios da área sob uma curva para resolver
Encontre a área sob a curva $latex y=2x^2+3$ de $latex x=-1$ até $latex x=2$.
Escreva a resposta na caixa.
Veja também
Interessado em aprender mais sobre integrais de funções? Você pode olhar para estas páginas: