A derivada da função secante inversa é igual a 1/(|x|√(x2-1)). Podemos provar esta derivada usando o teorema de Pitágoras e a álgebra.
Neste artigo, vamos aprender como derivar a função secante inversa. Veremos alguns princípios básicos, uma comparação gráfica da função e sua derivada, e alguns exemplos.
CÁLCULO
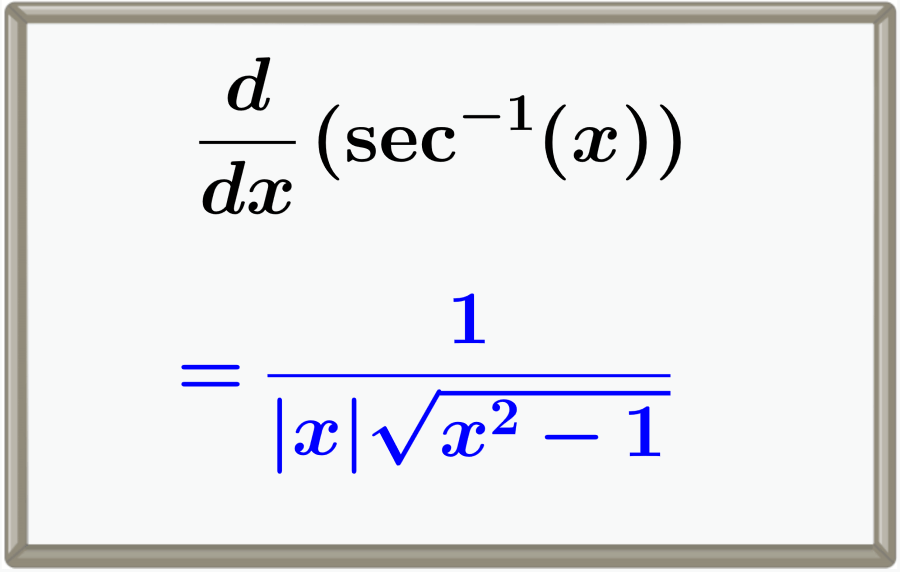
Relevante para…
Aprender sobre a prova e os gráficos da derivada de arco sec de x.
CÁLCULO
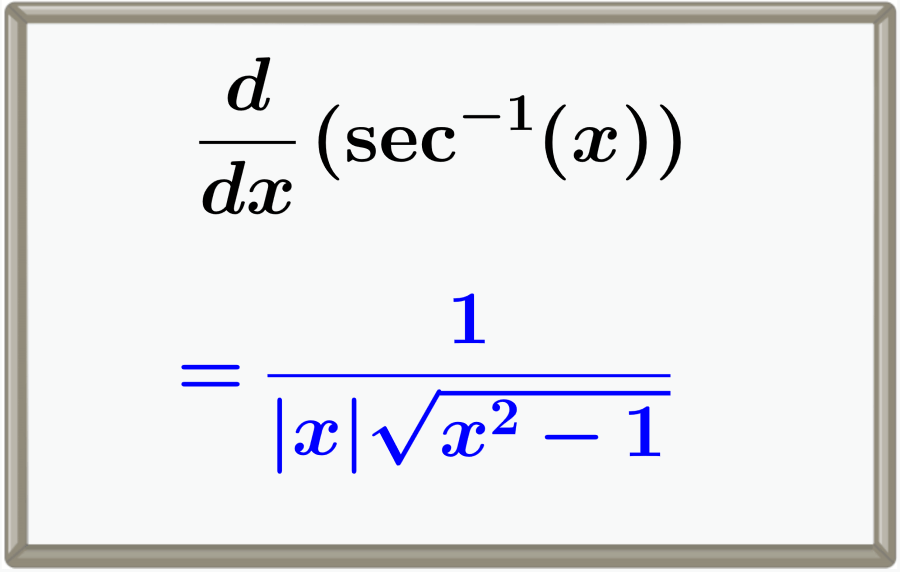
Relevante para…
Aprender sobre a prova e os gráficos da derivada de arco sec de x.
Evite confusão no uso de arcsec(x), $latex \sec^{-1}(x)$, $latex \frac{1}{\sec(x)}$, $latex \sec^{n}(x)$
É importante não cairmos na possível confusão que podemos ter ao usar diferentes denotações $latex \text{arcsec}(x)$, $latex \sec^{-1}{(x)}$, $latex \frac{1 }{\sec{(x)}}$ e $latex \sec^{n}{(x)}$, pois pode levar a erros de derivação.
Resumindo a definição desses símbolos, temos
$latex \text{arcsec}(x) = \sec^{-1}{(x)}$
Os símbolos $latex \text{arcsec}$ e $latex \sec^{-1}$ são usados alternadamente ao calcular a secante inversa. $latex \text{arcsecant}$ é comumente usado como símbolo verbal para a função secante inversa, enquanto $latex \sec^{-1}$ é usado como símbolo matemático para a função secante inversa para uma configuração mais formal.
No entanto, no caso da denotação $latex \sec^{-1}{(x)}$, devemos considerar que $latex -1$ não é um expoente algébrico de uma secante. O $latex -1$ usado para a secante inversa representa que a secante é inversa e não elevada a $latex -1$.
Portanto,
$latex \sec^{-1}{(x)} \neq \frac{1}{\sec{(x)}}$
E dado como $latex \sec^{2}{(x)}$ ou $latex \sec^{n}{(x)}$, onde n é qualquer expoente algébrico de uma secante não inversa, você NÃO DEVE usar a fórmula da secante inversa, pois nesses dados, tanto 2 quanto qualquer expoente n são tratados como expoentes algébricos de uma secante não inversa.
Prova da derivada da função arco secante
Nesta prova, usaremos principalmente os conceitos de triângulo retângulo, o teorema de Pitágoras, a função trigonométrica de secante e tangente e álgebra básica. Como na figura anterior como exemplo de referência para um determinado triângulo retângulo, suponha que temos esse mesmo triângulo $latex \Delta ABC$, mas desta vez, vamos alterar as variáveis para uma ilustração mais simples.
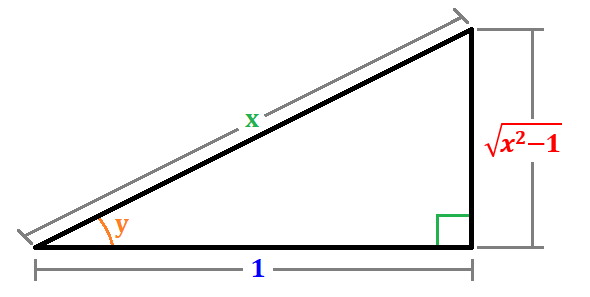
onde para cada unidade de um lado adjacente ao ângulo y, existe um lado $latex \sqrt{x^2-1}$ oposto ao ângulo y e uma hipotenusa x.
Usando esses componentes de um triângulo retângulo, podemos encontrar o ângulo y usando Cho-Sha-Cao, particularmente a função secante usando a hipotenusa x e seu lado adjacente.
$latex \sec{(\theta)} = \frac{hyp}{adj}$
$latex \sec{(y)} = \frac{x}{1}$
$latex \sec{(y)} = x$
Agora, podemos derivar implicitamente essa equação usando a derivada trigonométrica da função secante para o lado esquerdo e a regra da potência para o lado direito. Ao fazer isso, temos
$latex \frac{d}{dx} (\sec{(y)}) = \frac{d}{dx} (x)$
$latex \frac{d}{dx} (\sec{(y)}) = 1$
$latex \frac{dy}{dx} (\sec{(y)}\tan{(y)}) = 1$
$latex \frac{dy}{dx} = \frac{1}{\sec{(y)}\tan{(y)}}$
Obtendo a tangente do ângulo y do nosso triângulo retângulo dado, temos
$latex \tan{(y)} = \frac{opp}{adj}$
$latex \tan{(y)} = \frac{\sqrt{x^2-1}}{1}$
$latex \tan{(y)} = \sqrt{x^2-1}$
Então podemos substituir $latex \sec{(y)}$ e $latex \tan{(y)}$ na diferenciação implícita de $latex \sec{(y)} = x$
$latex \frac{dy}{dx} = \frac{1}{\sec{(y)}\tan{(y)}}$
$latex \frac{dy}{dx} = \frac{1}{(x) \cdot \left(\sqrt{x^2-1}\right)}$
$latex \frac{dy}{dx} = \frac{1}{x\sqrt{x^2-1}}$
Agora temos que
$latex \sec{(y)} = x$
e também
$latex hypothenuse = x$
Sabemos que uma hipotenusa negativa não pode existir. Portanto, $latex \sec{(y)}$ neste caso não pode ser negativo. É por isso que o multiplicando x no denominador da derivada da secante inversa deve ser considerado um valor absoluto.
$latex \frac{dy}{dx} = \frac{1}{|x|\sqrt{x^2-1}}$
Portanto, isolando o ângulo y algebricamente e obtendo sua derivada, temos
$latex \sec{(y)} = x$
$latex y = \sec^{-1}{(x)}$
$latex \frac{dy}{dx} = \frac{d}{dx} \left( \sec^{-1}{(x)} \right)$
$latex \frac{dy}{dx} = \frac{1}{|x|\sqrt{x^2-1}}$
que agora é a fórmula derivada da secante inversa de x.
Agora, para a derivada de uma secante inversa de qualquer função diferente de x, podemos aplicar a derivada da fórmula da secante inversa junto com a fórmula da regra da cadeia. Ao fazer isso, temos
$latex \frac{dy}{dx} = \frac{d}{du} \sec^{-1}{(u)} \cdot \frac{d}{dx} (u)$
$latex \frac{dy}{dx} = \frac{1}{|u|\sqrt{u^2-1}} \cdot \frac{d}{dx} (u)$
onde $latex u$ é qualquer função diferente de x.
Gráfico do arco secante de x vs. a derivada do arco secante de x
O gráfico da função
$latex f(x) = \sec^{-1}{(x)}$
é ilustrado como
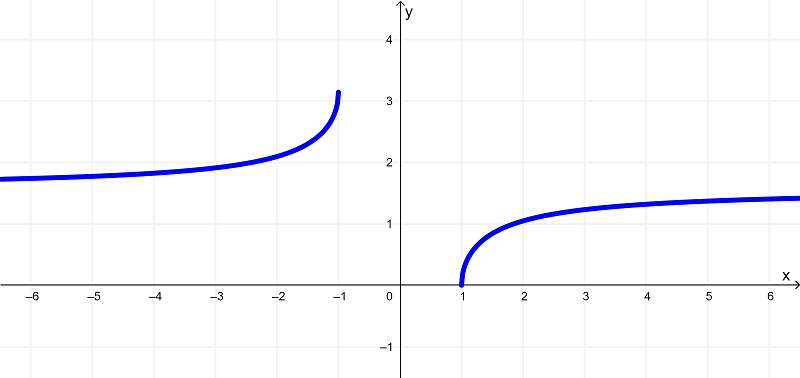
E diferenciando $latex f(x) = \sec^{-1}{(x)}$, obtemos
$latex f'(x) = \frac{1}{|x|\sqrt{x^2-1}}$
que tem o seguinte gráfico
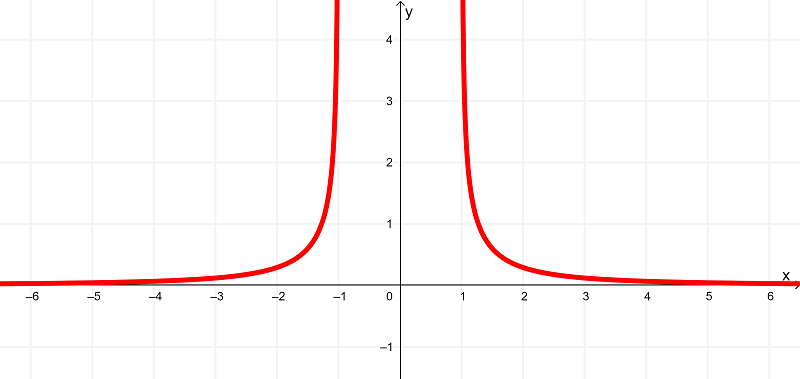
Ilustrando os dois gráficos em um, temos
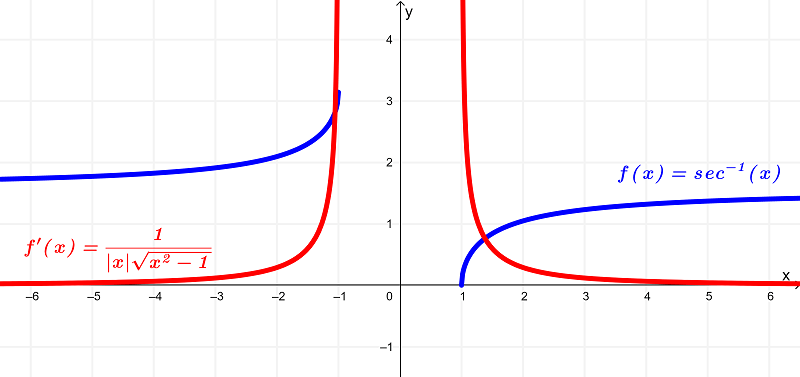
Usando os gráficos, vemos que a função original $latex f(x) = \sec^{-1}{(x)}$ tem um domínio de
$latex (-\infty,-1] \cup [1,\infty )$ ou todos os números reais, exceto $latex -1 < x < 1$
e existe dentro da imagem de
$latex [0,\frac{\pi}{2}\big) \cup \big(\frac{\pi}{2},\pi]$ ou $latex 0 \leq y \leq \pi$ exceto $latex \frac{\pi}{2}$
enquanto a derivada $latex f'(x) = \frac{1}{|x|\sqrt{x^2-1}}$ tem um domínio de
$latex (-\infty,-1) \cup (1,\infty)$ ou todos os números reais, exceto $latex -1 \leq x \leq 1$
e existe dentro da imagem de
$latex (0,\infty)$ ou $latex y > 0$
Exemplos
Nos exemplos a seguir, veremos como derivar as funções de secante inversa composta.
EXEMPLO 1
Qual é a derivada de $latex f(x) = \sec^{-1}(2x)$?
Solução
Uma vez que temos uma função secante inversa composta, podemos usar a regra da cadeia para a derivar.
Assim, consideramos $latex u=2x$ como a função interna e temos $latex f(u)=\sec^{-1}(u)$ e aplicando a regra da cadeia, temos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{|u|\sqrt{u^2-1}} \times 2$$
Em seguida, inserimos $latex u=2x$ de volta na função e temos:
$$\frac{dy}{dx}=\frac{2}{|2x|\sqrt{(2x)^2-1}}$$
$$\frac{dy}{dx}=\frac{2}{|2x|\sqrt{4x^2-1}}$$
EXEMPLO 2
Encontre a derivada da função $latex F(x) = \sec^{-1}(x^2-5)$
Solução
Para usar a regra da cadeia, escrevemos a função secante inversa como $latex f (u) = \sec^{-1}(u)$, onde $latex u = x^2-5$.
Então, começamos por encontrar a derivada da função externa $latex f(u)$:
$$\frac{d}{du} ( \sec^{-1}(u) ) = \frac{1}{|u|\sqrt{u^2-1}}$$
Agora, calculamos a derivada da função interna $latex g(x)=u=x^2-5$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(x^2-5)$$
$$\frac{d}{dx}(g(x)) = 2x$$
Depois, temos que multiplicar a derivada da função externa pela derivada da função interna:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = \frac{1}{|u|\sqrt{u^2-1}} \cdot 2x$$
Finalmente, substituímos $latex u$ de volta e simplificamos:
$$\frac{dy}{dx} = \frac{1}{|x^2-5|\sqrt{(x^2-5)^2-1}} \cdot 2x$$
$$\frac{dy}{dx} = \frac{2x}{|x^2-5|\sqrt{(x^2-5)^2-1}}$$
$$F'(x) = \frac{2x}{|x^2-5|\sqrt{x^4-10x^2+24}}$$
EXEMPLO 3
Encontre a derivada de $latex f(x) = \sec^{-1}(\sqrt{x})$
Solução
Neste caso, a função interna é $latex u=\sqrt{x}$. Considerando que podemos escrevê-lo como $latex u=x^{\frac{1}{2}}$, sua derivada é:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Se aplicarmos a regra da cadeia com $latex f(u)=\sec^{-1}(u)$, temos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\frac{1}{|u|\sqrt{u^2-1}} \times \frac{1}{2}x^{-\frac{1}{2}}$$
Substituindo $latex u=\sqrt{x}$ e simplificando, temos:
$$\frac{dy}{dx}=\frac{1}{|\sqrt{x}|\sqrt{(\sqrt{x})^2-1}} \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=\frac{1}{|\sqrt{x}|\sqrt{x-1}} \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=\frac{1}{|\sqrt{x}|\sqrt{x-1}\sqrt{x}}$$
$$\frac{dy}{dx}=\frac{1}{|\sqrt{x}|\sqrt{x(x-1)}}$$
Prática de derivadas de funções secante inversa composta


Veja também
Interessado em aprender mais sobre derivadas de funções trigonométricas inversas? Veja estas páginas:
- Derivada do arco tan (tangente inversa) – Demonstração e Gráficos
- Derivada do arco seno (seno inverso) – Demonstração e Gráficos
- Derivada do arco cos (cosseno inverso) – Demonstração e Gráficos
- Derivada de arc csc (Cossecante Inverso) – Demonstração e Gráficos
- Derivada de arco cot (cotangente inversa) – Demonstração e gráficos



