Seno, cosseno e tangente são as funções trigonométricas mais importantes. Para obter os gráficos das funções trigonométricas precisamos conhecer o período, a fase e a amplitude. Os gráficos de cossecante, secante e cotangente são obtidos considerando que são funções recíprocas de seno, cosseno e tangente, respectivamente.
Neste artigo, aprenderemos sobre as representações gráficas das funções seno, cosseno e tangente. Também aprenderemos sobre a amplitude, fase e período dessas funções.
ALGEBRA
Relevante para…
Aprender a representar graficamente as funções trigonométricas fundamentais.
ALGEBRA
Relevante para…
Aprender a representar graficamente as funções trigonométricas fundamentais.
Gráfico do seno
A função seno é uma das funções trigonométricas fundamentais. Podemos escrever $latex y= \sin(x)$ ou $latex f(x)=\sin(x)$. A seguir está o gráfico do seno:
A função seno tem as seguintes características:
- As raízes ou zeros de $latex y=\sin(x)$ são múltiplos de π.
- O gráfico do seno passa pela origem, pois quando x é 0, temos $latex \sin(0)=0$.
- O período da função seno é 2π.
- A altura da curva em cada ponto é igual ao valor da função seno em cada ponto.
- O valor máximo da função é 1 quando $latex x=\frac{\pi}{2}$.
- O valor mínimo da função é -1 quando $latex x=\frac{3\pi}{2}$.
Gráfico do cosseno
Para o cosseno, podemos escrever $latex y=\cos(x)$ ou $latex f(x)=\cos(x)$. A seguir está o gráfico do cosseno:
A seguir estão as características do gráfico da função cosseno:
- Temos essa identidade $latex \sin(x+\frac{\pi}{2}) =\cos (x)$.
- O gráfico do cosseno é o gráfico que obtemos se movermos para o gráfico do seno
$latex \frac{\pi}{2}$ unidades à esquerda. - As raízes ou zeros da função cosseno são os múltiplos de π/2.
- O gráfico do seno cruza o eixo y no ponto (0, 1).
- O período da função cosseno é 2π.
- O valor máximo da função é 1 quando $latex x=0$.
- O valor mínimo da função é -1 quando x é π.
Podemos observar as seguintes semelhanças entre gráficos de seno e gráficos de cosseno:
- Ambos produzem a mesma curva, que é movida ao longo do eixo x.
- Ambos têm amplitude de 1.
- Ambos têm um período de 2π ou 360 °.
O gráfico a seguir nos mostra uma comparação das funções seno e cosseno:
Gráfico da tangente
O gráfico da tangente é completamente diferente em comparação com o gráfico do seno e do cosseno. O gráfico da função tangente tem valores que variam de infinito negativo a infinito positivo e cruza o eixo x ao longo de um período de π radianos:
A seguir estão as características da função tangente:
- As raízes ou zeros da função são os múltiplos de π.
- O gráfico da tangente passa pela origem.
- O gráfico da tangente tem amplitude indefinida porque a curva vai ao infinito.
- O período da função seno é π ou 180 °.
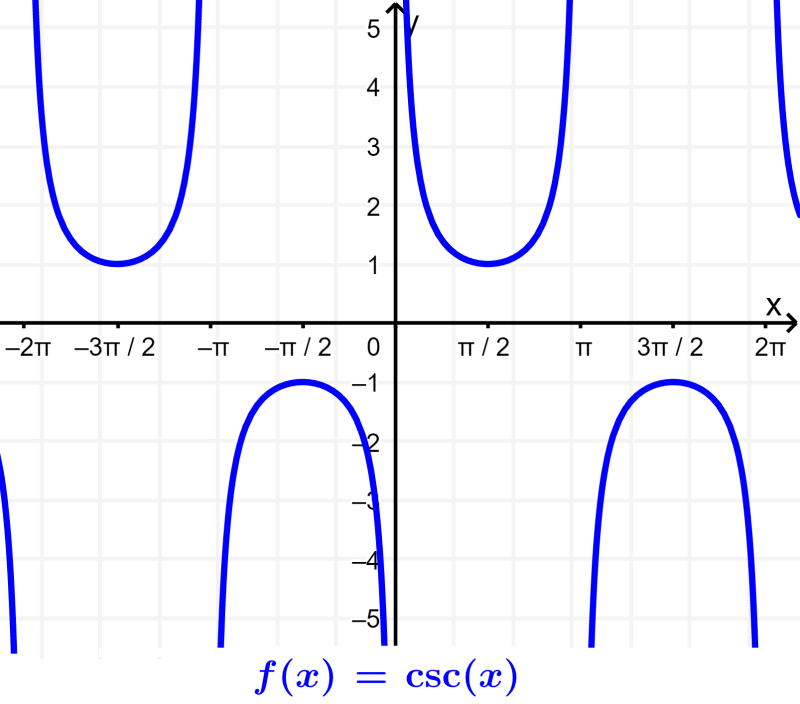
Gráfico da cossecante
A cossecante é a função recíproca do seno. Isso significa que a função cossecante é obtida dividindo 1 pelo seno. Assim, a função cossecante torna-se indefinida quando o seno é igual a 0 (múltiplos de π).
A seguir estão algumas características importantes da função cossecante:
- A cosecante não tem raízes ou zeros. Podemos ver que o gráfico não toca o eixo x.
- A cossecante é indefinida em múltiplos de π. Ou seja, tem assíntotas nesses pontos.
- A imagem da função cossecante são todos os números reais, exceto -1<y<1.
- O gráfico da cossecante tem uma amplitude indefinida.
- O período da função cossecante é 2π ou 360°.
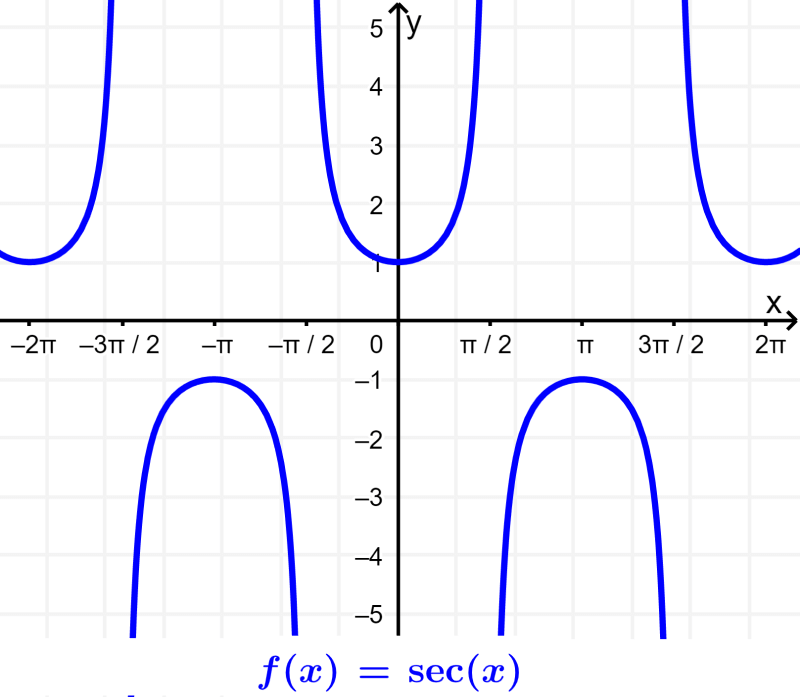
Gráfico da secante
A secante é a função recíproca do cosseno. Ou seja, podemos obter a função secante dividindo 1 pelo cosseno. Assim, a função secante torna-se indefinida quando o cosseno é igual a 0 (π/2±nπ, onde n é um inteiro).
A seguir temos algumas características importantes da função secante:
- A função secante nunca toca o eixo x. Isso significa que não tem raízes ou zeros.
- A secante tem assíntotas em múltiplos de π/2, pois é indefinida nesses pontos.
- O intervalo da função secante são todos os números reais, exceto -1<y<1.
- A secante tem amplitude indefinida.
- O período da função secante é 2π ou 360°.
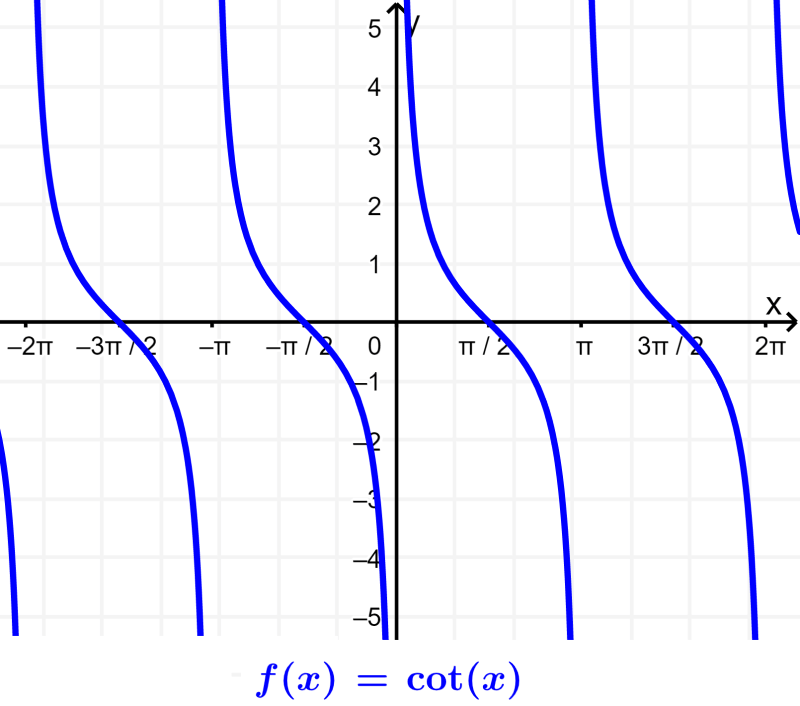
Gráfico da cotangente
A cotangente é a função recíproca da tangente. Ou seja, a cotangente é equivalente a 1 dividido pela função tangente. Assim, a função cotangente resulta indefinida quando a tangente é igual a 0 (múltiplos de π).
A seguir temos algumas características importantes da função cotangente:
- Os zeros ou raízes da cotangente estão localizados em π/2±nπ, onde n é um número inteiro.
- A cotangente é indefinida em múltiplos de π. Ou seja, tem assíntotas nesses pontos.
- A imagem da cotangente são todos os números reais.
- O gráfico da cotangente tem uma amplitude indefinida.
- O período da função cotangente é π ou 180°.
Amplitude das funções trigonométricas
A amplitude é a altura da linha central de uma função trigonométrica até seu ponto máximo ou mínimo. A amplitude é o valor absoluto pelo qual uma função trigonométrica é multiplicada.
A amplitude também pode ser medida tomando a altura do ponto mais alto do ponto mais baixo e dividindo por 2. A amplitude nos diz quão alto ou baixo é o gráfico de uma função trigonométrica.
Período das funções trigonométricas
O período é a medida de dois pontos equivalentes no gráfico, por exemplo, um ponto máximo, até o próximo ponto equivalente. A seguir está uma representação gráfica do período da função seno:
Fase das funções trigonométricas
Fase é uma medida do movimento horizontal de uma função trigonométrica a partir de sua posição original. A seguir está uma representação gráfica da fase da função seno:
Como representar graficamente as funções trigonométricas?
Existem vários métodos que podem ser usados para representar graficamente funções trigonométricas. A seguir está uma explicação detalhada de um dos métodos mais eficientes para representar graficamente funções trigonométricas.
Para traçar o gráfico das funções trigonométricas, devemos começar convertendo a função dada para a forma geral $latex a\sin(bx-c)+d$. Desta forma, podemos encontrar facilmente os diferentes parâmetros como amplitude, fase, período e translação vertical, onde:
- $latex |a|=$ amplitude
- $latex \frac{2\pi}{|b|}=$ período
- $latex \frac{c}{b}=$ fase
- $latex d=$ movimento vertical
Da mesma forma, podemos encontrar o gráfico do cosseno usando a forma $latex a\cos(bx-c)+d$.
Os gráficos das funções trigonométricas fundamentais são mostrados abaixo em sua forma básica:
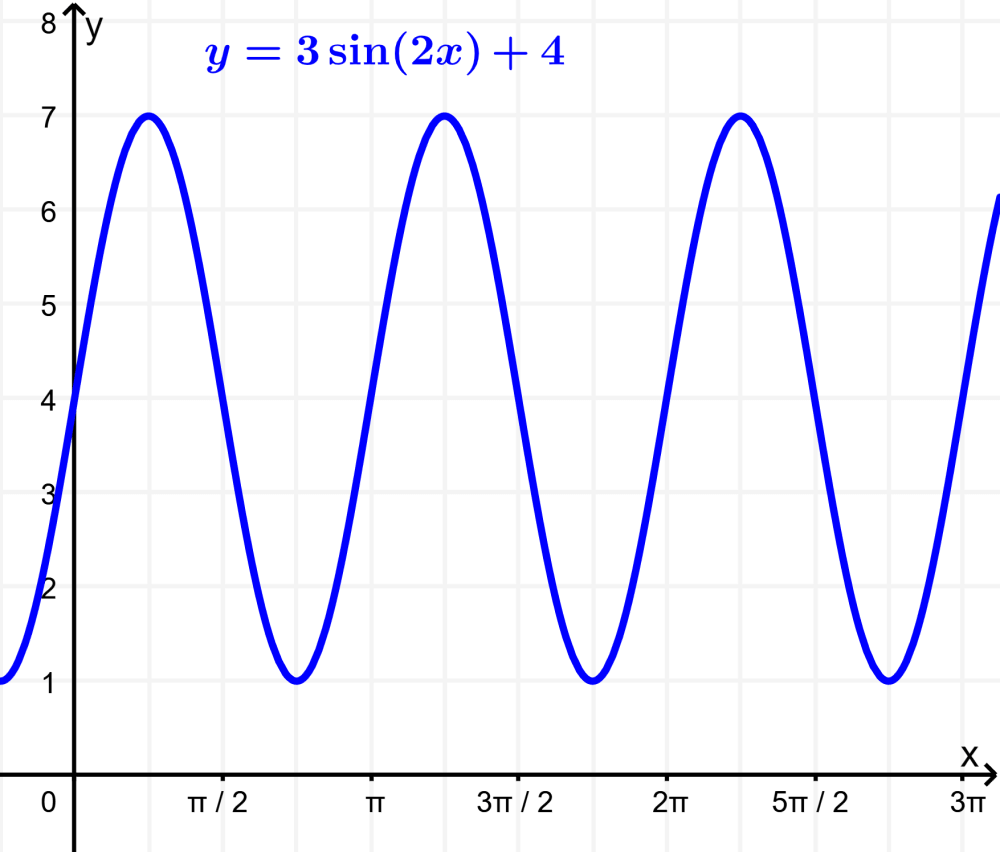
EXEMPLO 1
Represente graficamente a função $latex y=3\sin(2x)+4$.
Solução:
- A amplitude é 3, então a distância entre os valores mínimo e máximo é 6.
- O número de ondas é 2. Cada onda tem um período de 360° ÷ 2 = 180°.
- O gráfico é movido 4 unidades para cima.
- O ponto máximo é (3×1)+4 = 7 e o ponto mínimo é (3×-1)+4 = 1.
- O período é $latex \frac{2\pi}{2}=\pi$
O gráfico é parecido com este:
EXEMPLO 2
A seguir está o gráfico da função $latex y=3 \sin (2(x+3)) – 2$.
Nesta função, temos:
- Amplitude: $latex A=2$
- Período: $latex \text{periodo}=\frac{2\pi}{B}=\frac{2\pi}{2}=\pi$
- Fase: $latex C=-3$
- Movimento vertical: $latex D=-2$
Veja também
Você quer aprender mais sobre gráficos de funções? Olha para estas páginas: