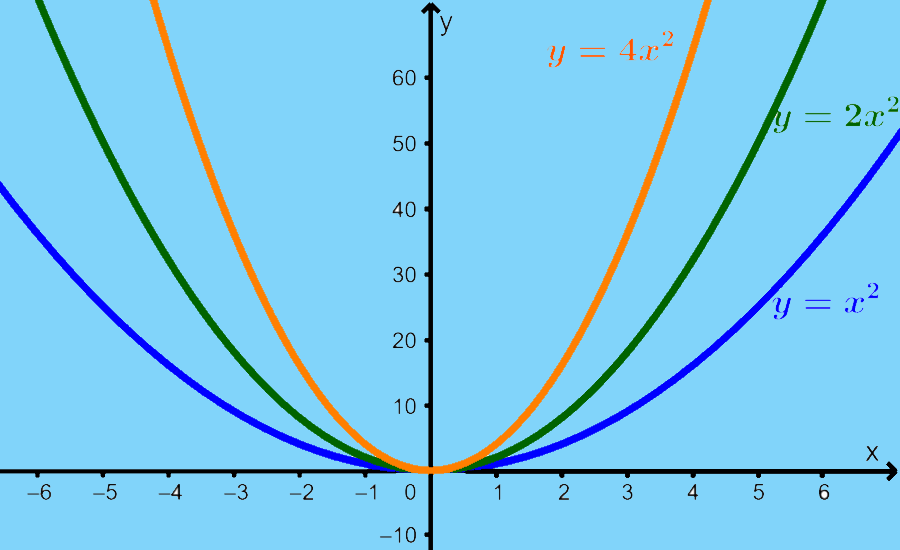
O gráfico de uma função quadrática tem uma curva em forma de U e é chamado de parábola. Podemos representar graficamente uma função quadrática usando seus pontos-chave, como suas interceptações em x, seu vértice e seu eixo de simetria. As partes de uma parábola nos dão informações importantes sobre uma função quadrática.
Neste artigo, aprenderemos sobre as diferentes partes dos gráficos de funções quadráticas e representaremos graficamente essas funções na forma de vértice e na forma padrão.
Partes de parábolas
Lembre-se de que uma função quadrática tem a forma $latex f (x) = a{{x}^2}+bx+c$, onde a, b e c são constantes e $latex a \ne 0$.
Os gráficos das funções quadráticas são em forma de U, conforme mostrado abaixo:
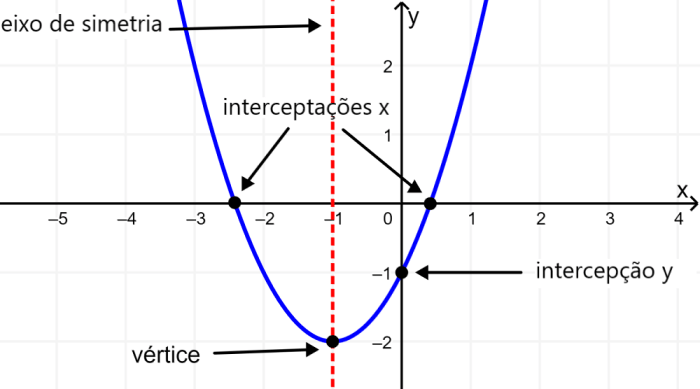
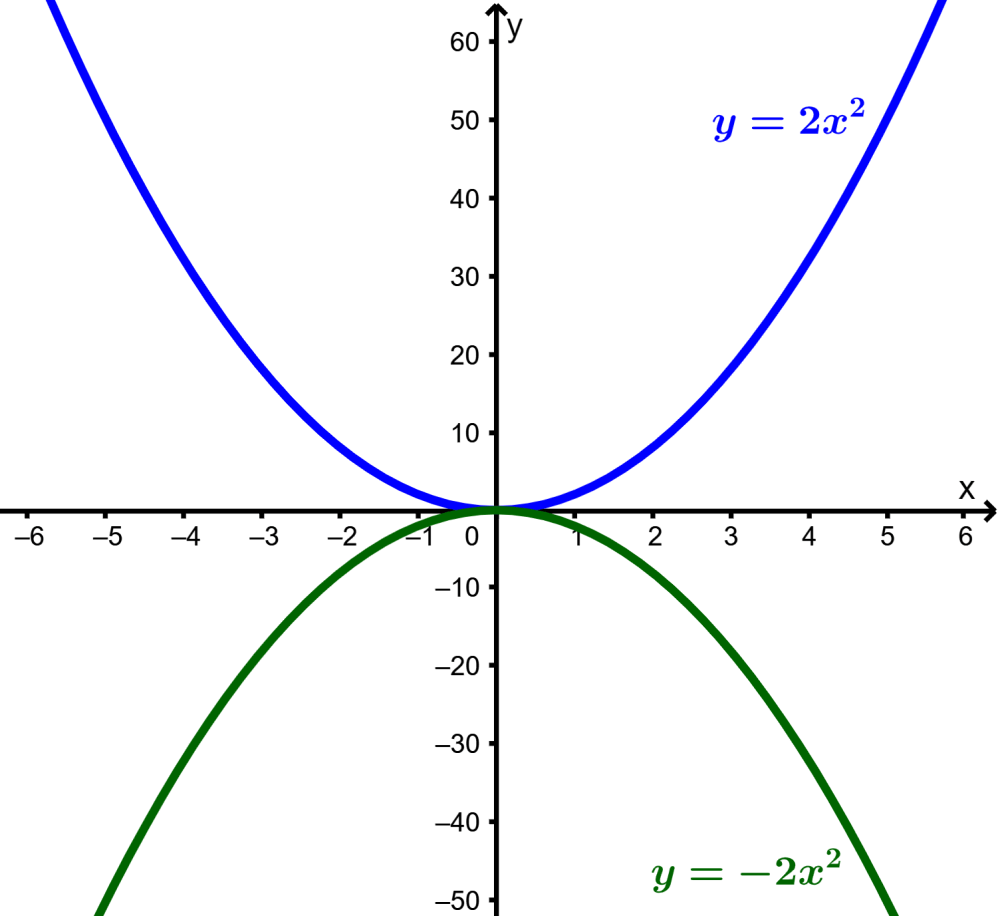
O sinal no coeficiente a determina se o gráfico abre para cima ou abre para baixo. Se $latex a> 0$, o gráfico abre para cima e se $latex a<0$, o gráfico abre para baixo.
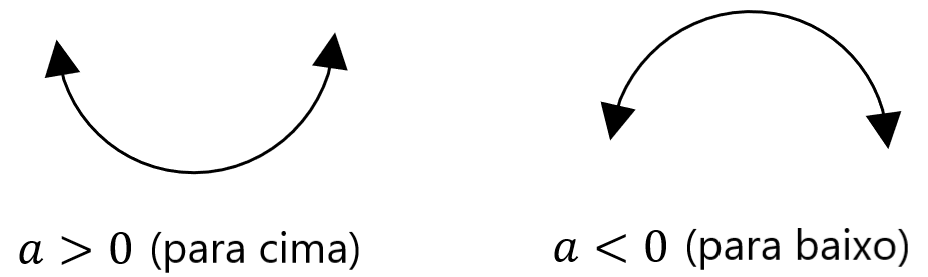
As parábolas possuem características diferentes que determinam sua forma e sua localização no plano cartesiano. Essas características são o vértice, o eixo de simetria, a interceptação y e as interceptações x.
Vértice
O vértice é o ponto extremo no gráfico de uma função quadrática, ou seja, é o ponto mais alto ou o ponto mais baixo. Se a parábola se abre para cima, o vértice representa o ponto mais baixo e se a parábola se abre para baixo, o vértice representa o ponto mais alto.
Eixo de simetria
Todas as parábolas são simétricas em relação a uma linha vertical chamada eixo de simetria. Esta linha vertical passa pelo vértice.
Interceptação y
A interceptação y é o ponto onde a parábola cruza o eixo y. Para todos os gráficos de funções quadráticas, há uma única interceptação y. Se houvesse mais interceptações y, o gráfico não representaria uma função.
Interceptações x
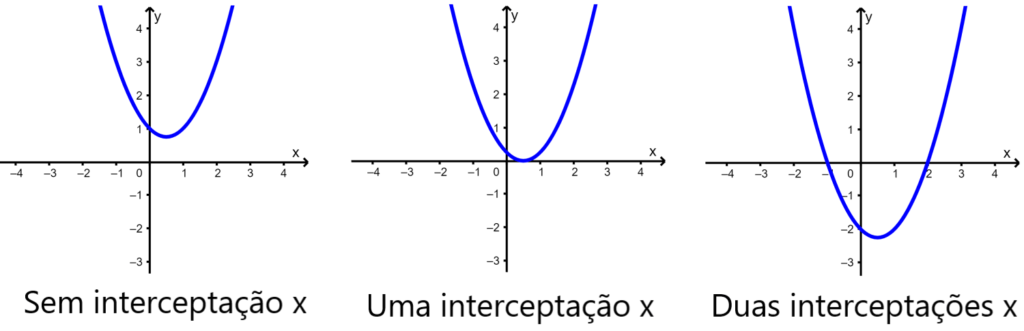
As interceptações são os pontos onde a parábola cruza o eixo x. Os interceptos em x representam os zeros ou raízes da função quadrática, ou seja, os valores de x quando temos $latex x = 0$. É possível ter zero interceptações x, uma interceptação x e duas interceptações x. O número de interceptações depende da localização do gráfico da função quadrática. Quando a parábola tem dois interceptos x, o vértice sempre fica entre esses interceptos devido à simetria do gráfico.
Interpretação gráfica das soluções de funções quadráticas
Podemos encontrar as raízes das funções quadráticas algebricamente ou graficamente.
Para encontrar as raízes algebricamente, podemos usar a fórmula quadrática $latex x=\frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}$. Também podemos encontrar as raízes graficamente, fazendo várias observações do gráfico de uma função quadrática.
Vejamos a conexão entre encontrar raízes algebricamente e graficamente com o gráfico da função $latex f(x)={{x}^{2}}+x-2$:
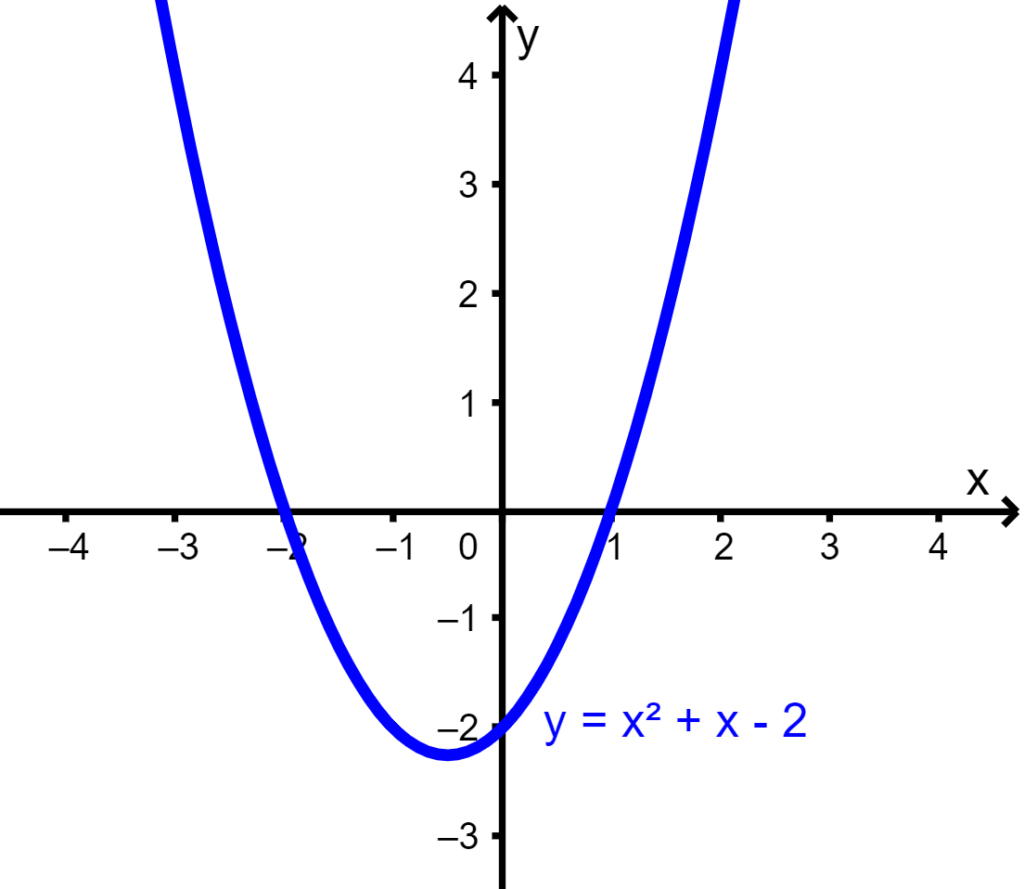
Podemos ver que o gráfico cruza o eixo x nos pontos (-2, 0) e (1, 0). Sabemos que as interceptações em x representam as raízes da função quadrática, então $latex x=-2$ e $latex x=1$ são as raízes.
Agora vamos encontrar as raízes de $latex f(x)={{x}^{2}}+x-2$ algebricamente. Podemos usar a fórmula quadrática com os coeficientes $latex a=1, b=1, c=-2$.
$latex x=\frac{{-1\pm \sqrt{{{{1}^{2}}-4\left( 1 \right)\left( {-2} \right)}}}}{{2\left( 1 \right)}}$
$latex x=\frac{{-1\pm \sqrt{9}}}{2}$
$latex x=\frac{{-1\pm 3}}{{2}}$
Portanto, temos dois valores possíveis para x: $latex x=\frac{{-1+3}}{{2}}$ e $latex x=\frac{{-1-3}}{{2}}$. Simplificando esses valores, obtemos $latex x=1$ e $latex x=-2$. Esses são os mesmos valores que encontramos graficamente.
EXEMPLOS
Encontre as raízes da função $latex f(x)={{x}^{2}}+2x+3$ algebricamente e graficamente:
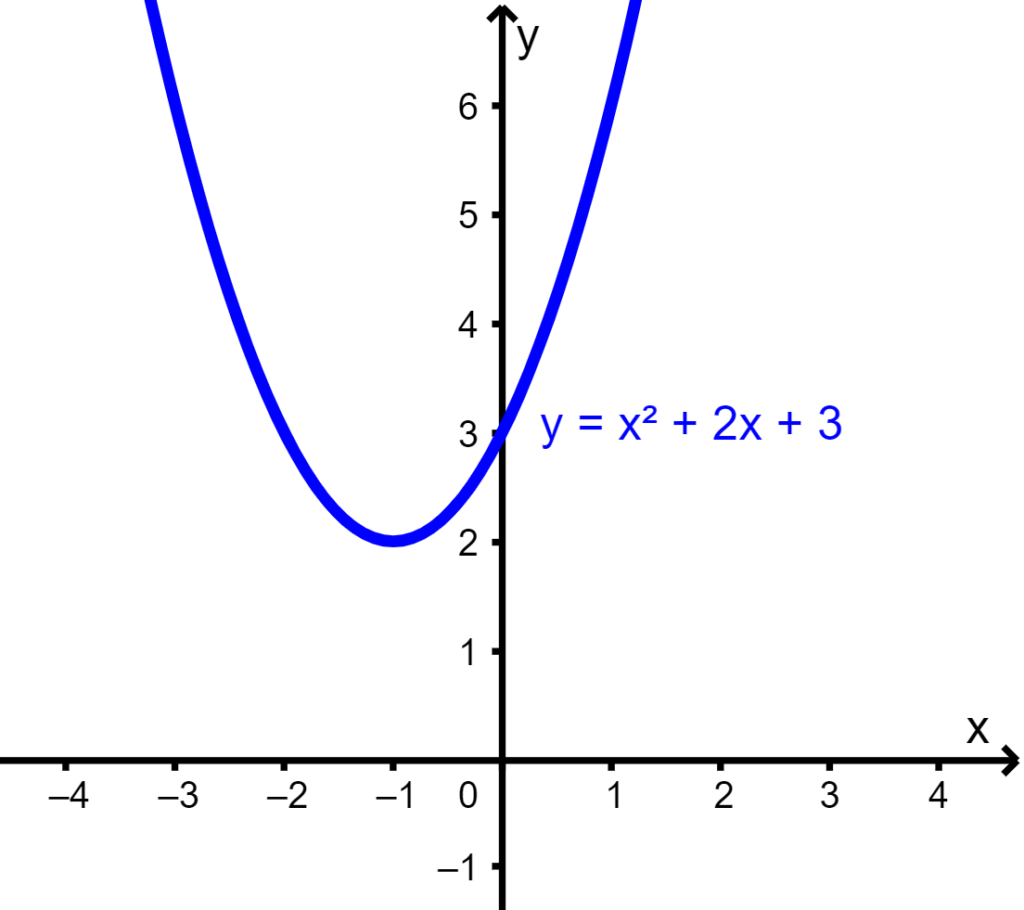
Podemos ver que o gráfico não cruza o eixo x, portanto, não possui raízes reais. Podemos verificar isso algebricamente.
Usaremos a fórmula quadrática com os coeficientes $latex a=1, b=2, c=3$.
$latex x=\frac{{-2\pm \sqrt{{{{2}^{2}}-4\left( 1 \right)\left( {3} \right)}}}}{{2\left( 1 \right)}}$
$latex x=\frac{{1\pm \sqrt{-9}}}{2}$
Nós observamos que temos $latex \sqrt{-8}$, que não é um número real. Isso significa que a função quadrática não tem raízes reais.
Gráficos de funções quadráticas na forma de vértice
A forma de vértice de uma função quadrática nos permite encontrar o vértice do gráfico facilmente.
As equações quadráticas podem ser apresentadas de diferentes maneiras. Por exemplo, já vimos sua forma canónica:
$latex f\left( x \right)=a{{x}^{2}}+bx+c$
Outra forma comum é a forma do vértice:
$latex f\left( x \right)=a{{(x-h)}^{2}}+k$
Nesta forma, o vértice é o ponto $latex (h, k)$. Como vimos anteriormente, o coeficiente $latex a$ determina se a parábola abre para cima ou para baixo.
Transformar da forma do vértice para a forma canónica
Para transformar uma função quadrática escrita na forma de vértice para a forma canónica, simplesmente expandimos a expressão quadrada e combinamos termos semelhantes. Por exemplo, o seguinte quadrática:
$latex f\left( x \right)={{(x-5)}^{2}}+4$
Pode ser reescrita assim:
$latex f\left( x \right)=(x-5)(x-5)+4$
$latex f\left( x \right)={{x}^{2}}-5x-5x+25+4$
$latex f\left( x \right)={{x}^{2}}-10x+29$
Transformar da forma canónica para a forma do vértice
Isso é um pouco mais difícil e temos que usar um processo chamado “completar o quadrado”.
Quando temos $latex a=1$
Suponha que queremos escrever $latex f\left( x \right)={{x}^{2}}+2x+3$ na forma de vértice. Observamos que o coeficiente do termo $latex {{x}^{2}}$ é 1.Quando for esse o caso, olhamos para o coeficiente do termo x e pegamos sua metade. Então nós elevamos esse número ao quadrado. Ou seja, neste caso temos 2, pegando a sua metade temos 1 e ao quadrado, temos 1. Então, somamos e subtraímos este número como mostrado abaixo:
$latex f\left( x \right)=({{x}^{2}}+2x+1)+3-1$
Aqui, adicionamos e subtraímos o mesmo número, portanto, não alteramos realmente a função. Agora, a expressão entre parênteses pode ser escrita como um quadrado e temos:
$latex f\left( x \right)={{(x+1)}^{2}}+2$
Nesta forma, o vértice é $latex (-1, 2)$.
Quando temos $latex a\ne 1$
Isso é um pouco mais difícil do que o caso anterior, mas podemos usar a mesma ideia para transformar a função. Suponha que queremos escrever $latex f\left( x \right)=2{{x}^{2}}+12x-4$ na forma de vértice. Agora, o coeficiente do termo $latex {{x}^{2}}$ é 2. Podemos fatorar 2 dos dois primeiros termos:
$latex f\left( x \right)=2({{x}^{2}}+6x)-4$
Então, completamos o quadrado entre parênteses. Notamos que metade de 6 é 3 e o quadrado é 9, então adicionamos e subtraímos 9 dentro dos parênteses:
$latex f\left( x \right)=2({{x}^{2}}+6x+9-9)-4$
e resolvemos o seguinte:
$latex f\left( x \right)=2({{(x+3)}^{2}}-9)-4$
$latex f\left( x \right)=2{{(x+3)}^{2}}-18-4$
$latex f\left( x \right)={{(x+3}^{2}}-11$
Então, o vértice do gráfico é $latex (-3, -11)$.
Gráficos de funções quadráticas na forma canónica
Uma função quadrática na forma $latex f(x) =a{{x}^2}+bx+c$ está na forma canónica. Independentemente do formato, o gráfico de uma função quadrática é uma parábola. Por exemplo, o seguinte é o gráfico de $latex f(x) = {{x}^2} + 2x-4$.
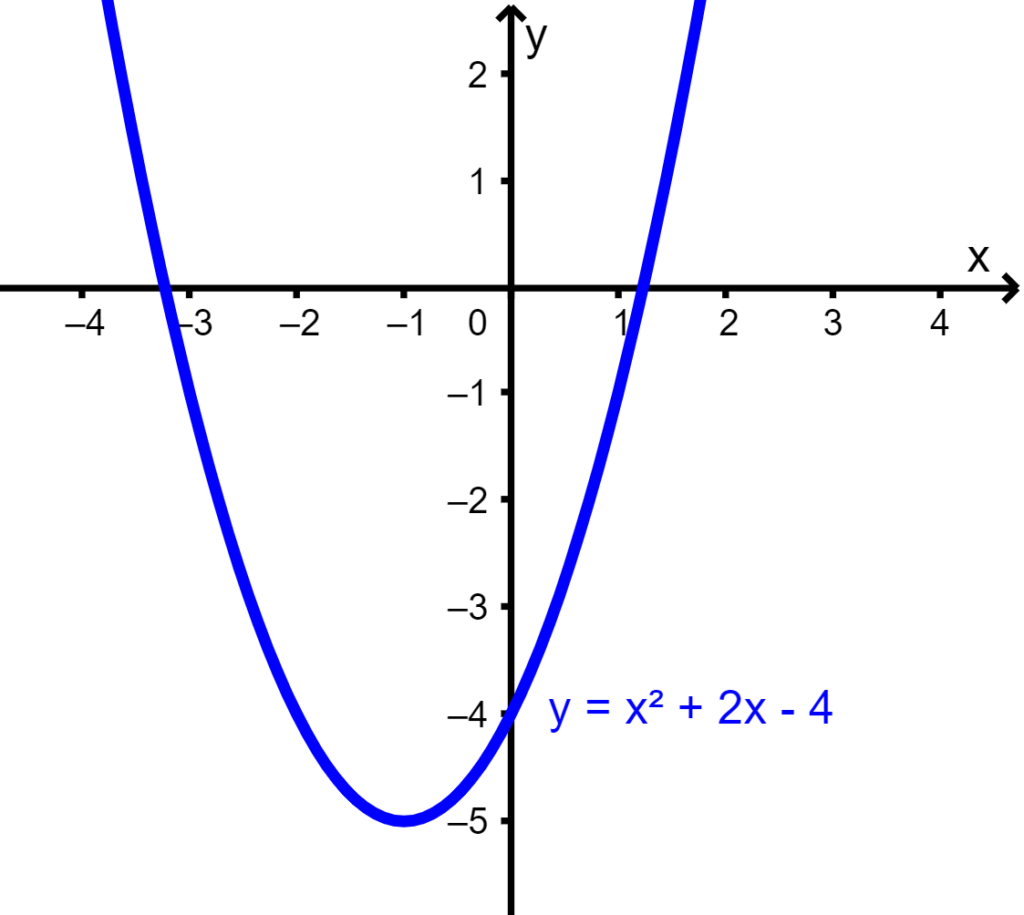
Cada coeficiente de uma função quadrática tem um impacto na forma e na localização do gráfico no plano cartesiano.
Coeficiente de $latex {{x}^2}$, a
O coeficiente a controla a taxa de aumento ou diminuição da função do vértice. Quanto maior e positivo for a, mais rápido a função quadrática crescerá e o gráfico parecerá ficar “mais fino”.
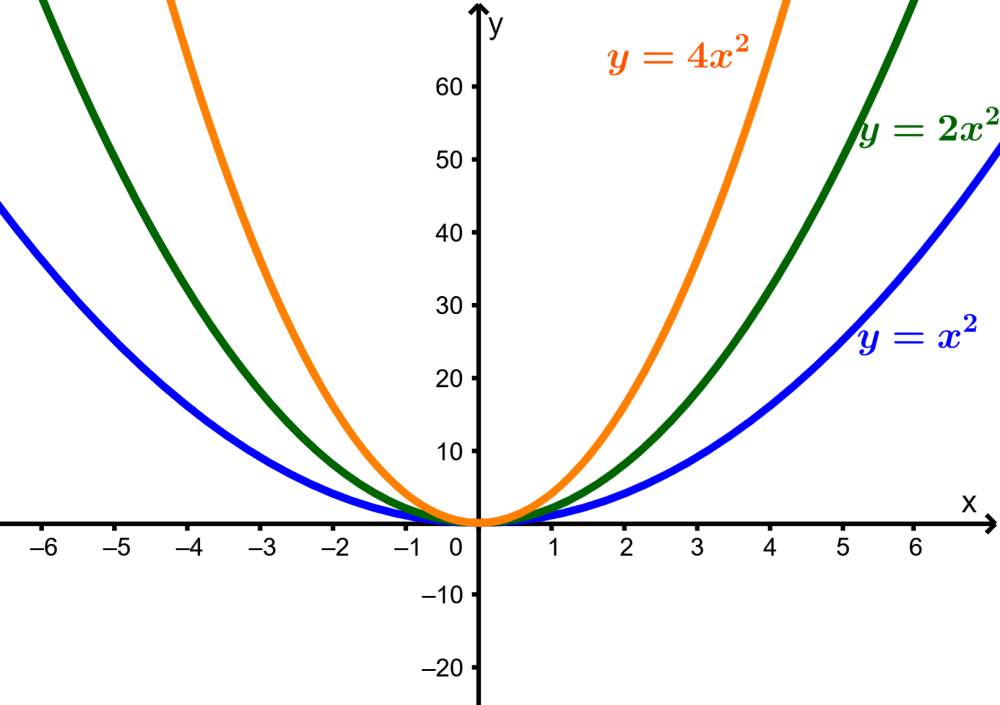
O coeficiente a também controla onde a parábola será aberta. Se tivermos $latex a>0$, o gráfico se abrirá para cima e se tivermos $latex a<0$, o gráfico se abrirá para baixo.
Eixo de simetria
Os coeficientes aeb controlam o eixo de simetria e a coordenada x do vértice da parábola. Podemos encontrar o eixo de simetria de uma parábola da seguinte forma:
$latex x=-\frac{b}{2a}$
Por exemplo, na parábola $latex f (x)=3{{x}^2}-6x+2$, temos $latex a=3, ~b=-6$, então temos $latex x=-\frac{- 6}{2(3)}=1$. O vértice tem uma coordenada x de 1:
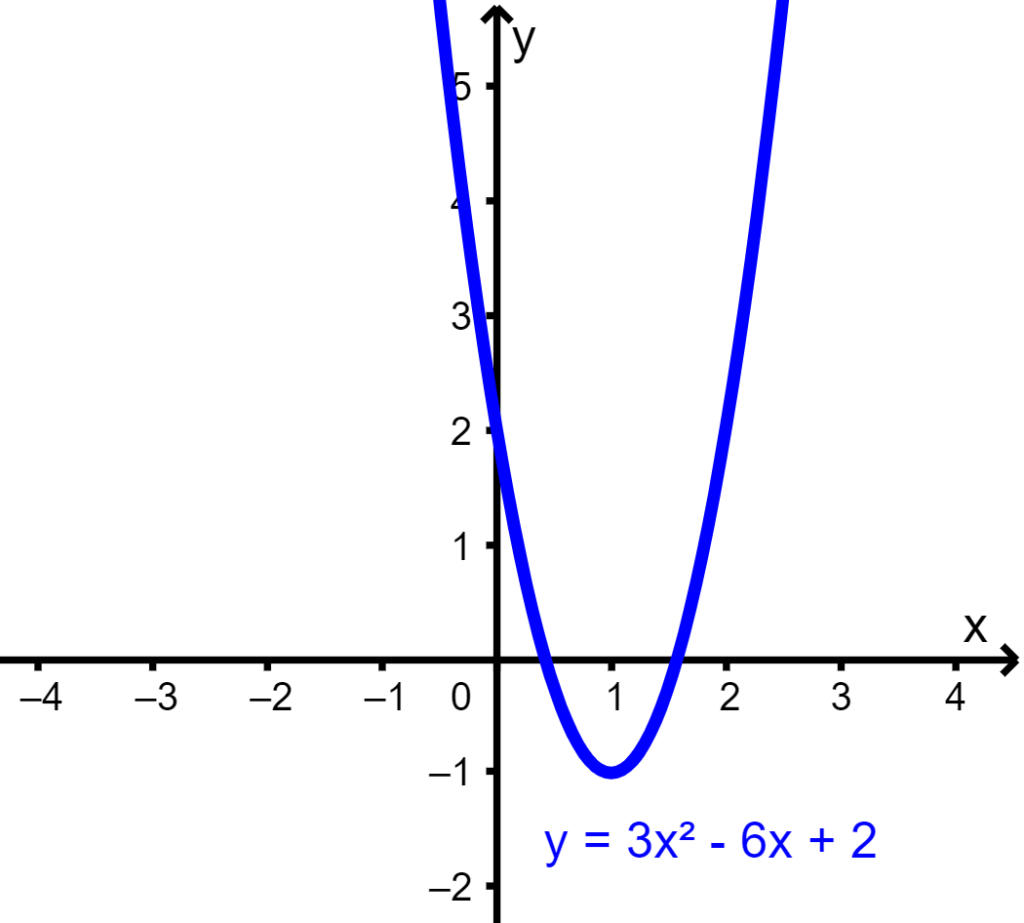
A interceptação em y da parábola
O coeficiente c controla a altura da parábola. Este é o ponto onde a parábola intercepta o eixo y. O ponto (0, y) é a interceptação y da parábola. Nesse caso, $latex c=2$ e a parábola intercepta o eixo y no ponto (0, 2).
Veja também
Você quer aprender mais sobre gráficos de funções? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
