A função logarítmica $latex y=\log _{b}x$ é definida como a função inversa da função exponencial $latex y={{b}^x}$. Sabendo disso, podemos representar graficamente as funções logarítmicas observando a relação entre as funções logarítmicas e as funções exponenciais.
Neste artigo, vamos aprender a fazer gráficos de funções logarítmicas. Veremos gráficos com translação horizontais e verticais.
Termos importantes
Antes de começar com os gráficos das funções logarítmicas, é importante que nos familiarizemos com alguns termos que serão utilizados.
Domínio de uma função
O domínio de uma função é o conjunto de valores que podemos substituir na função para obter respostas aceitáveis. Ou seja, o domínio são todos os valores possíveis para x.
Imagem de uma função
A imagem é o conjunto de valores que obtemos substituindo os valores no domínio da variável.
Assíntotas
Uma assíntota é uma linha da qual uma curva se aproxima à medida que os valores x ou y tendem ao infinito. Temos três tipos de assíntotas: vertical, horizontal e inclinada. A assíntota vertical é o valor de x pelo qual a função cresce sem limites quando se aproxima desse valor. A assíntota horizontal é um valor de y do qual a função se aproxima à medida que os valores de x crescem sem limites. Assíntotas inclinadas são equações lineares das quais a função se aproxima à medida que os valores de x tendem ao infinito.
Como obter gráficos de funções logarítmicas?
Podemos representar graficamente uma função logarítmica examinando o gráfico de uma função exponencial e, em seguida, trocando os valores de x e y.
- O gráfico de uma função exponencial $latex y={{b}^x}$ tem as seguintes características:
- O domínio de uma função exponencial são todos os números reais. Ou seja, os valores de x variam de infinito negativo a infinito positivo.
- O intervalo é composto por todos os números positivos reais. Ou seja, de 0 a infinito positivo.
- O gráfico de uma função exponencial normalmente passa pelo ponto (0, 1), o que significa que esse ponto é a interceptação y.
- O gráfico de uma função exponencial $latex y={{b}^x}$ tem uma assíntota horizontal em $latex y=0$.
- Se tivermos $latex 1>b>0$, a função diminui da esquerda para a direita e é chamada de decaimento exponencial.
- Se tivermos $latex b>1$, o gráfico aumenta da esquerda para a direita e é chamado de crescimento exponencial.
Usando cada uma das características mencionadas, podemos deduzir características equivalentes para as funções logarítmicas:
- O domínio de uma função logarítmica são todos os números reais positivos, de 0 a infinito positivo.
- O intervalo de uma função exponencial são todos os números reais.
- O gráfico de uma função logarítmica passa pelo ponto (1, 0).
- O gráfico de uma função logarítmica tem uma assíntota vertical em $latex x=0$.
- Se tivermos $latex 1>b>0$, o gráfico diminuirá da esquerda para a direita.
- Se tivermos b> 1, o gráfico crescerá da esquerda para a direita.
Gráficos de funções logarítmicas básicas
Podemos considerar uma função logarítmica básica como uma função que não possui movimentos horizontais ou verticais.
Podemos representar graficamente as funções logarítmicas básicas seguindo estas etapas:
Passo 1: Todas as funções logarítmicas básicas passam pelo ponto (1, 0), portanto, começamos traçando esse ponto.
Passo 2: Sabemos que o gráfico tem uma assíntota em $latex x=0$, de modo que traçá-lo.
Passo 3: Se a base da função for maior que 1, o gráfico aumenta da esquerda para a direita. Se a base da função estiver entre 0 e 1, o gráfico diminui da esquerda para a direita.
EXEMPLO 1
Represente graficamente a função logarítmica $latex y=\log_{2}x$.
Solução: Começamos colocando um ponto em (1, 0). Sabemos que a função logarítmica deve ter o domínio de (0, infinito) e a imagem de (-infinito, infinito).
Como a função logarítmica $latex y =\log_{2}x$ tem uma base maior que 1, incrementamos a curva da esquerda para a direita, conforme mostrado abaixo.
A assíntota horizontal não pode ser exibida, pois está localizada exatamente no eixo x.
EXEMPLO 2
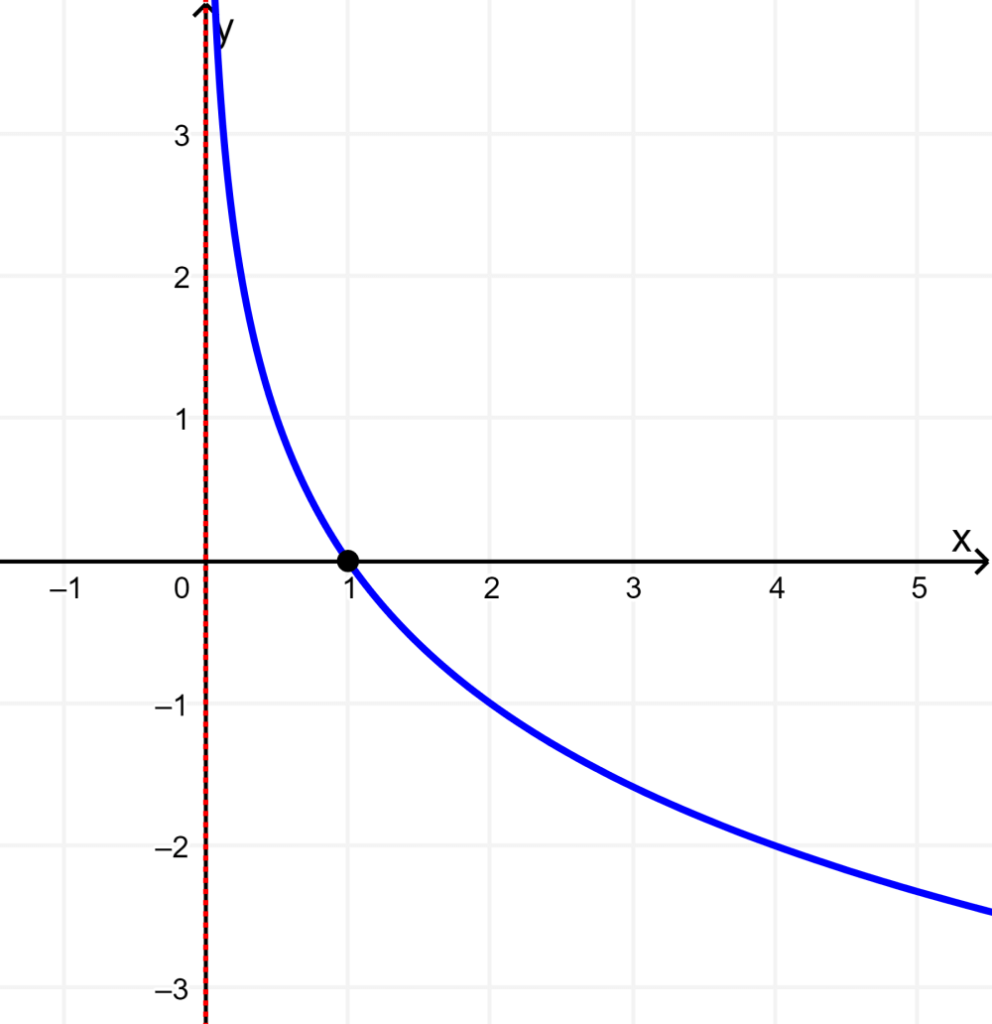
Represente graficamente a função logarítmica $latex y =\log_{0,5}x$.
Solução: Da mesma forma, colocamos um ponto em (1, 0). A função possui o mesmo domínio e imagem da anterior. O domínio é (0, infinito) e a imagem é (-infinito, infinito).
A assíntota vertical está localizada exatamente no eixo y.
Nesse caso, a base da função $latex y=\log_{0,5}x$ é menor que 1, mas maior que 0, então a função diminui da esquerda para a direita.
Gráficos de funções logarítmicas com movimento horizontal
As funções logarítmicas com movimento horizontal têm a forma $latex y=\log _{b}(x-h)$, onde h é o movimento horizontal. Ao mover o gráfico horizontalmente, produzimos as seguintes alterações:
- A interceptação x se move para a direita ou esquerda por uma distância que corresponde ao valor de h.
- A assíntota vertical se move na mesma distância.
- O domínio da função também é afetado.
EXEMPLO 1
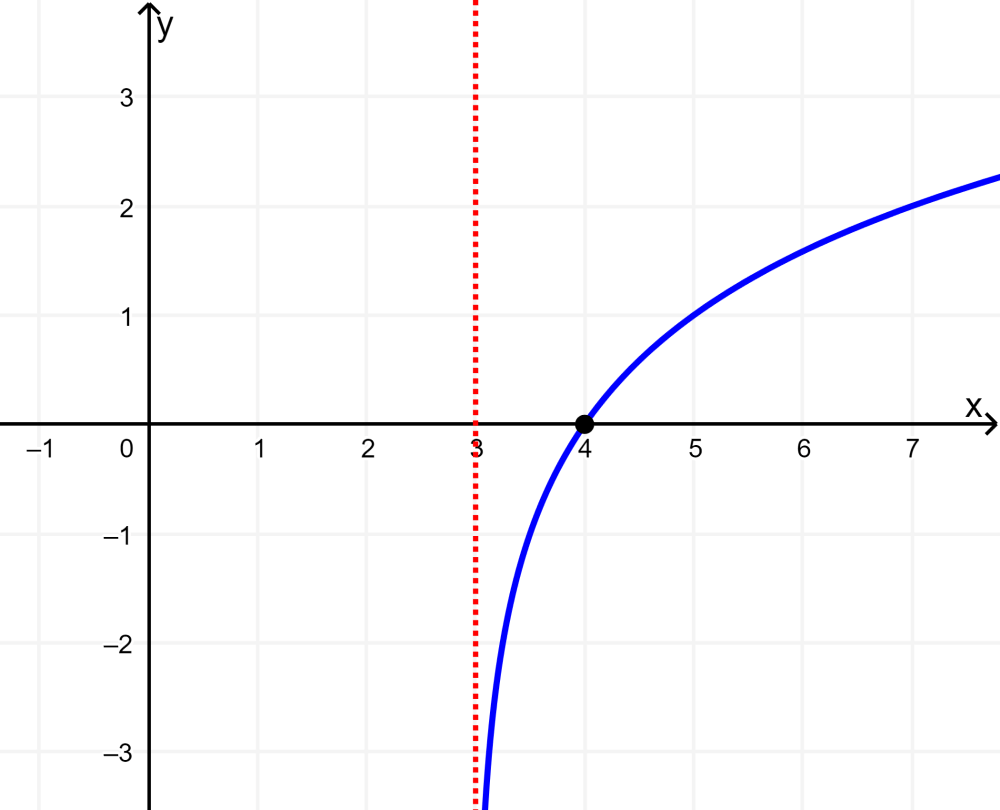
Represente graficamente a função logarítmica $latex y=\log_{2}(x-3)$.
Solução: A interceptação x está localizada em (4, 0). A função tem o domínio (3, infinito) e a imagem é (-infinito, infinito).
A assíntota vertical está localizada em $latex x=3$.
A base da função é maior que 1, então a função cresce da esquerda para a direita.
EXEMPLO 2
Represente graficamente a função logarítmica $latex y=\log_{0,5}(x + 3)$.
Solução: A interceptação x está localizada em (-2, 0). A função possui o domínio (-3, infinito) e a imagem é (-infinito, infinito).
A assíntota vertical está localizada em $latex x=-3$.
Nesse caso, a base da função $latex y=\log_{0,5}x$ é menor que 1, mas maior que 0, então a função diminui da esquerda para a direita.
Gráficos de funções logarítmicas com movimento vertical
Uma função logarítmica com movimento vertical tem a forma $latex y=\log_{b}(x)+k$, onde k é o movimento vertical. Com um movimento vertical no gráfico, produzimos o seguinte:
- A interceptação x se move para cima ou para baixo em uma distância de k.
EXEMPLO
Represente graficamente a função logarítmica $latex y=\log_{2}(x)+3$.
Solução: A função logarítmica possui o domínio (0, infinito) e a imagem é (-infinito, infinito).
A assíntota vertical está localizada em $latex x=0$.
A função cresce da esquerda para a direita, pois sua base é maior que 1.
Gráficos de funções logarítmicas com movimento horizontal e vertical
Uma função logarítmica com movimento horizontal e vertical tem a forma $latex y=\log_{b}(x-h) + k$, onde h é o movimento horizontal e k é o movimento vertical.
EXEMPLO 1
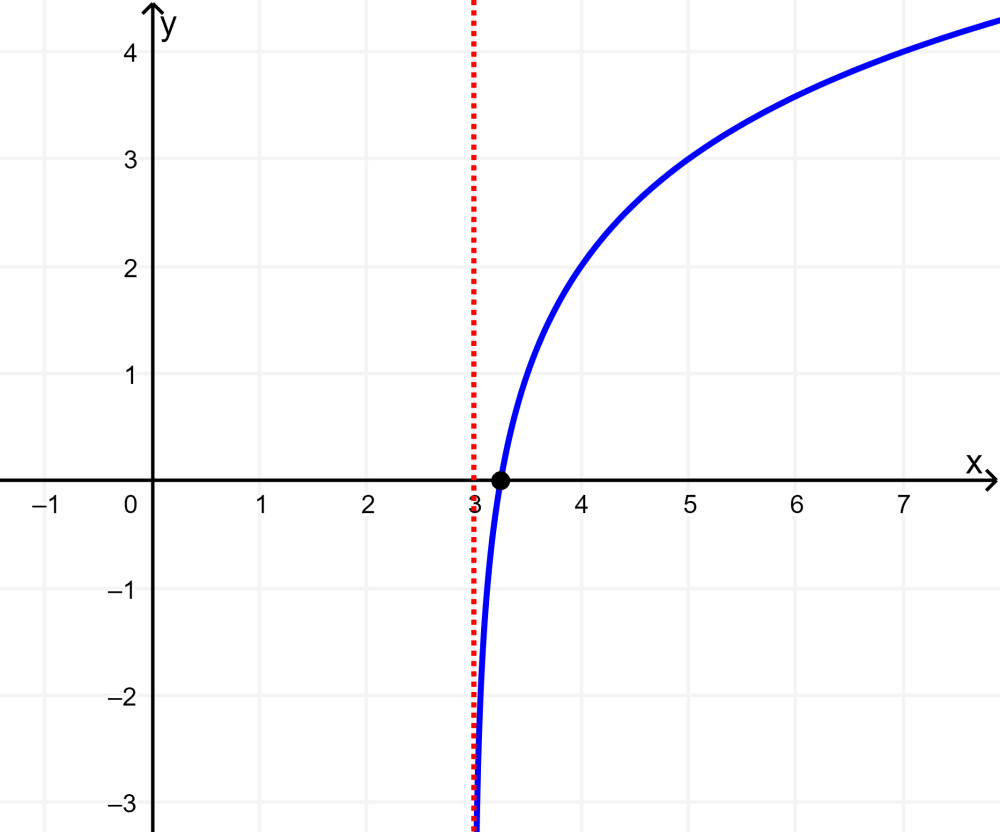
Represente graficamente a função logarítmica $latex y=\log_{2}(x-3)+2$.
Solução: O gráfico se move 3 unidades para a direita e 2 unidades para cima. A função tem o domínio (3, infinito) e a imagem é (-infinito, infinito).
A assíntota vertical está localizada em $latex x=3$.
A base da função é maior que 1, então a função cresce da esquerda para a direita.
EXEMPLO 2
Represente graficamente a função logarítmica $latex y=\log_{0,5}(x + 2) -3$.
Solução: A função original é movida 2 unidades para a esquerda e 3 unidades para baixo.
A assíntota vertical está localizada em $latex x=-2$.
Na função $latex y=\log_{0,5} x$, a base é menor que 1 e maior que 0, então a função diminui da esquerda para a direita.
Veja também
Você quer aprender mais sobre gráficos de funções? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
