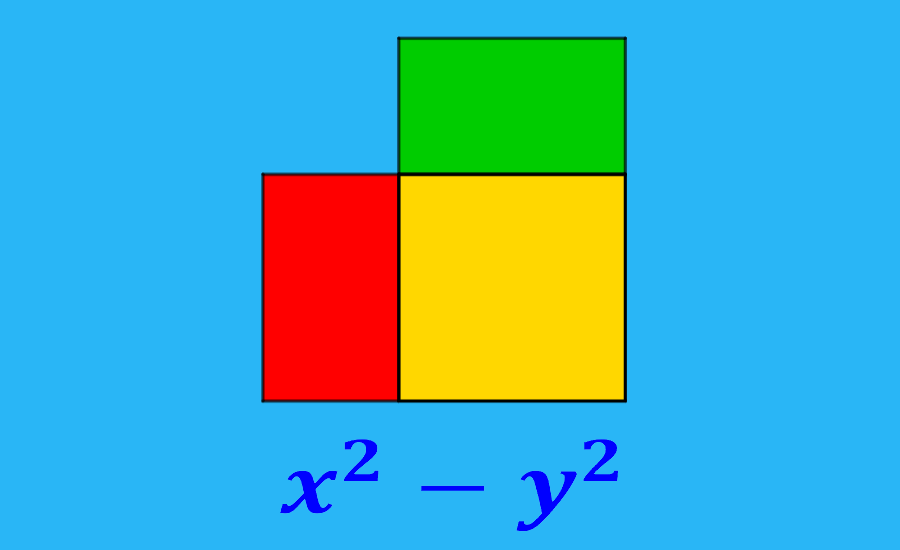Quando aprendemos a fatorar, geralmente exploramos fórmulas importantes ao mesmo tempo. Uma dessas fórmulas é a diferença de quadrados. O teorema da diferença de quadrados nos diz que se tivermos uma expressão da forma a²-b², isso é equivalente a (a+b)(a–b).
Neste artigo, aprenderemos mais sobre a diferença de quadrados, veremos como fatorar usando esta fórmula e veremos exercícios com respostas para entender os conceitos.
O qué é a diferença dos quadrados?
A diferença dos quadrados é um teorema que nos diz se uma equação quadrática pode ser escrita como um produto de dois binômios, onde um, mostra a diferença das raízes quadradas e o outro, mostra a soma das raízes quadradas.
Uma diferença de quadrados é algo que se parece com $latex x^2-4$. Isso ocorre porque $latex 2^2=4$, então, na verdade temos $latex x^2-2^2$, o qual é uma diferença de quadrados.
Fórmula da diferença de quadrados
A fórmula da diferença de quadrados é uma expressão algébrica usada para expressar a diferença entre dois valores quadrados. Uma diferença de quadrados é expressa na forma:
$latex a^2-b^2$
onde o primeiro e o último termos são quadrados perfeitos.
Fatorando a diferença de quadrados, temos:
$latex a^2-b^2=(a+b)(a-b)$
Isso é verdade porque $$(a+b)(a-b)=a^2+ab-ab-b^2=a^2-b^2$$
Como fatorar a diferença de quadrados?
A seguir estão os passos necessários para fatorar uma diferença de quadrados:
1. Fatore a expressão inicial se possível.
Determine se os termos têm um fator comum. Em caso afirmativo, fatore esse fator comum e não se esqueça de incluí-lo na resposta final. Por exemplo, $latex 2x^2-32=2(x^2-16)$.
2. Aplique a fórmula da diferença dos quadrados.
A fórmula para a diferença de quadrados é $latex a^2-b^2=(a+b)(a-b)$. Por exemplo, $latex 2(x^2-16)$ é igual a $latex 2(x+4)(x-4)$.
3. Fatore e simplifique o resultado final.
Determine se os demais fatores podem ser fatorados ou simplificados.
Exemplos resolvidos de diferença de quadrados
EXEMPLO 1
Fatore a expressão $latex {{x}^{2}}-9$.
Solução
Passo 1: Nesse caso, a expressão não precisa ser fatorada.
Passo 2: Para fatorar o problema na forma $latex (a+b)(a-b)$ precisamos determinar o valor que temos que elevar ao quadrado para obter $latex {{x}^{2}}$ e o valor que temos que elevar ao quadrado para obter 9.
Neste caso, temos x e 3, pois $latex (x)(x)={{x}^{2}}$ e $latex (3)(3)=9$.
$latex {{x}^{2}}-9$
$latex =(x+3)(x-3)$
Passo 3: A expressão está agora em sua forma mais simples.
EXEMPLO 2
Use a diferença de quadrados para fatorar $latex 4x^2-49$.
Solução
Passo 1: Os termos não têm um fator comum.
Passo 2: Para fatorar o problema na forma $latex (a+b)(a-b)$ precisamos determinar o valor que temos que elevar ao quadrado para obter $latex 4x^2$ e o valor que temos que elevar ao quadrado para obter 49 .
Neste caso, temos 2x e 7 porque $latex (2x)(2x)=4x^2$ e $latex (7)(7)=49$.
$latex 4x^2-49$
$latex =(2x+7)(2x-7)$
Passo 3: A expressão está agora em sua forma mais simples.
EXEMPLO 3
Fatore a expressão $latex 18x^2-98$.
Solução
Passo 1: Os termos têm um fator comum:
$latex 2(9x^2-49)$
Passo 2: Temos que determinar o valor que precisamos elevar ao quadrado para obter $latex 9x^2$ e o valor que precisamos elevar ao quadrado para obter 49.
Neste caso, temos 3x e 7 porque $latex (3x)(3x)=3x^2$ e $latex (7)(7)=49$.
$latex 2(9x^2-49)$
$latex =2(3x+7)(3x-7)$
Passo 3: A expressão está agora em sua forma mais simples.
EXEMPLO 4
Use a diferença de quadrados na expressão $latex 4x^2-64$.
Solução
Passo 1: Os termos têm um fator comum.
$latex 4(x^2-16)$
Passo 2: Precisamos encontrar o valor que temos que elevar ao quadrado para obter $latex x^2$ e o valor que precisamos elevar ao quadrado para obter 16.
Então, temos x e 4 porque $latex (x)(x)=x^2$ e $latex (4)(4)=16$.
$latex 4(x^2-16)$
$latex =4(x+4)(x-4)$
Passo 3: O resultado não pode mais ser simplificado.
EXEMPLO 5
Fatore a expressão $latex 16x^4-1$.
Solução
Passo 1: Não temos fatores comuns.
Passo 2: Precisamos encontrar o valor que temos que elevar ao quadrado para obter $latex 16x^4$ e o valor que temos que elevar ao quadrado para obter 1.
Neste caso, temos $latex 4x^2$ e 1 porque $latex (4x^2)(4x^2)=16x^4$ e $latex (1)(1)=1$.
$latex (4x^2+1)(4x^2-1)$
Passo 3: Um dos fatores é uma diferença de quadrados, então podemos fatorá-lo: precisamos determinar o valor que temos que elevar ao quadrado para obter $latex 4x^2$ e o valor que temos que elevar ao quadrado para obter 1.
Neste caso, temos $latex 2x$ e 1 porque $latex (2x)(2x)=4x^2$ e $latex (1)(1)=1$.
$latex (4x^2+1)(2x+1)(2x-1)$
Se você quiser explorar mais exemplos de diferença de quadrados, visite nosso artigo: Exercícios de Diferença de Quadrados Resolvidos e para Resolver.
Exercícios de prática de diferença de quadrados
Fatore a expressão $latex 4x^2-36$ usando a diferença de quadrados.
Escreva a resposta na caixa.
Veja também
Interessado em aprender mais sobre diferença de quadrados e outros tópicos algébricos? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
