Identidades Pitagóricas são identidades em trigonometria que são extensões do teorema de Pitágoras. As identidades Pitagóricas são úteis para simplificar expressões trigonométricas. Essas identidades são especialmente úteis para escrever expressões como uma função de seno ou cosseno, como as fórmulas de ângulo duplo.
A seguir, conheceremos as identidades de Pitágoras e aprenderemos a derivá-las a partir do teorema de Pitágoras. Em seguida, veremos alguns exercícios práticos onde aplicaremos essas identidades.
TRIGONOMETRIA
Relevante para…
Aprender sobre identidades pitagóricas com exercícios.
TRIGONOMETRIA
Relevante para…
Aprender sobre identidades pitagóricas com exercícios.
Quais são as identidades pitagóricas?
As identidades pitagóricas são equações que contem funções trigonométricas, verdadeiras para todos os valores substituídos nas variáveis. As identidades trigonométricas são especialmente úteis para simplificar expressões trigonométricas. As identidades Pitagóricas são derivadas do teorema de Pitágoras:
| $latex {{\sin}^2} (\theta)+{{\cos}^2} (\theta)=1$ |
Esta é a identidade pitagórica mais importante. Essa identidade é verdadeira para todos os valores de θ. Usando essa primeira identidade, podemos criar duas identidades Pitagóricas adicionais:
| $latex {{\tan}^2} (\theta)+1={{\sec}^2} (\theta)$ $latex 1+{{\cot}^2} (\theta)={{\csc}^2} (\theta)$ |
onde “tan” representa a função tangente, “sec” representa a função secante, “cot” representa a função cotangente e “csc” representa a função cossecante.
Como derivar as identidades pitagóricas?
Podemos derivar as identidades pitagóricas usando o círculo unitário. Lembre-se que o círculo unitário é um círculo com raio 1. Neste triângulo, as coordenadas x são representadas por $latex \cos(\theta)$ e as coordenadas y são representadas por $latex \sin(\theta)$ como mostrado no diagrama a seguir:
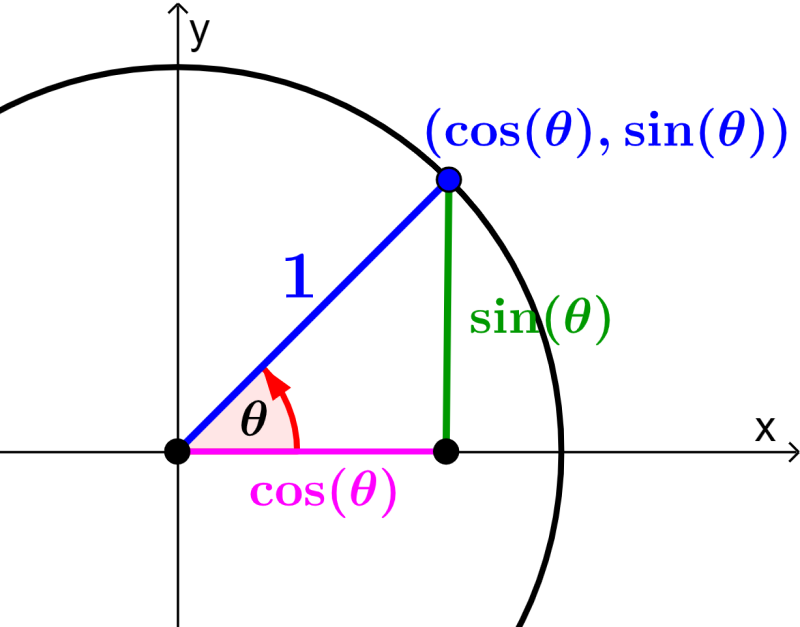
Vemos que os catetos do triângulo retângulo no círculo unitário têm os valores de $latex \sin(\theta)$ e $latex \cos(\theta)$. Além disso, a hipotenusa do triângulo é o raio do círculo, que é igual a 1. Então, usando o teorema de Pitágoras, temos:
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
Esta é a principal identidade Pitagórica. Usando essa identidade, podemos derivar duas identidades adicionais.
Começamos com a primeira identidade Pitagórica:
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
Dividimos cada termo por $latex {{\cos}^2}(\theta)$:
$$\frac{{{\sin}^2}(\theta)}{{{\cos}^2}(\theta)}+\frac{{{\cos}^2}(\theta)}{{{\cos}^2}(\theta)}=\frac{1}{{{\cos}^2}(\theta)}$$
Agora, sabemos que temos $latex \frac{\sin(\theta)}{\cos(\theta)}=\tan(\theta)$ e $latex \frac{1}{\cos(\theta) }= \sec(\theta)$. Então, substituindo e simplificando, temos:
$latex {{\tan}^2}(\theta)+1={{\sec}^2}(\theta)$
Se dividirmos por um valor diferente, podemos encontrar a terceira identidade Pitagórica. Começamos com a primeira identidade Pitagórica:
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
Dividimos cada termo por $latex {{\sin}^2}(\theta)$:
$$\frac{{{\sin}^2}(\theta)}{{{\sin}^2}(\theta)}+\frac{{{\cos}^2}(\theta)}{{{\sin}^2}(\theta)}=\frac{1}{{{\sin}^2}(\theta)}$$
Agora, podemos usar as relações $latex \frac{\cos(\theta)}{\sin(\theta)}=\cot(\theta)$ e $latex \frac{1}{\sin(\theta) } =\csc(\theta)$. Então, substituindo e simplificando, temos:
$latex 1+{{\cot}^2}(\theta)={{\csc}^2}(\theta)$
Exercícios resolvidos de identidade Pitagóricas
As identidades Pitagóricas derivadas acima são usadas para resolver os exercícios a seguir. Tente resolver os exercícios antes de olhar para a resposta.
EXERCÍCIO 1
Simplifique a expressão $latex \sin(x){{\cos}^2}(x)-\sin(x)$ usando as identidades Pitagóricas.
Solução
Esta expressão contém o seno e o cosseno, então podemos usar a identidade $latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$. Portanto, começamos fatorando a expressão dada:
$$\sin(x){{\cos}^2}(x)-\sin(x)=\sin(x)({{\cos}^2}(x)-1)$$
Podemos reescrever a identidade $latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$ da seguinte forma: $latex {{\cos}^2}(x )- 1=-{{\sin}^2}(x)$. Então, substituindo essa identidade, temos:
$$\sin(x)({{\cos}^2}(x)-1)=\sin(x)(-{{\sin}^2}(x))$$
$latex ={{\sin}^3}(x)$
EXERCÍCIO 2
Expresse a expressão trigonométrica $latex {{\csc}^2}(x)-\cot(x)-3$ na forma fatorada.
Solução
Podemos usar a identidade Pitagórica $latex 1+{{\cot}^2}(x)={{\csc}^2}(x)$. Então, substituindo, temos:
$latex {{\csc}^2}(x)-\cot(x)-3$
$latex =1+\cot^2(x)-\cot(x)-3$
$latex =\cot^2(x)-\cot(x)-2$
$latex =(\cot(x)-2)(\cot(x)+1)$
EXERCÍCIO 3
Simplifique a expressão trigonométrica $$({{\sec}^2}(x))(1-{{\sin}^2}(x))-(\frac{\sin(x)}{\csc(x) )}+\frac{\cos(x)}{\sec(x)})$$
Solução
Neste caso, temos que reconhecer que $latex \sec(x)=\frac{1}{\cos(x)}$ e $latex \csc(x)=\frac{1}{\sin(x) }$. Usando isso, temos:
$$({{\sec}^2}(x))(1-{{\sin}^2}(x))-(\frac{\sin(x)}{\csc(x)}+\frac{\cos(x)}{\sec(x)})$$
$$=({{\sec}^2}(x))(1-{{\sin}^2}(x))-({{\sin}^2}(x)+{{\cos}^2}(x))$$
Agora, usamos a identidade Pitagórica principal e temos:
$latex =({{\sec}^2}(x))({{\cos}^2}(x))-(1)$
$latex =1-1$
$latex =0$
EXERCÍCIO 4
Se temos $latex \tan(\theta)=\frac{1}{3}$, qual é o valor de $latex \frac{1}{{{\sin}^2}(\theta) }+\frac{1}{{{\cos}^2}(\theta)}$?
Solução
Podemos usar a segunda e a terceira identidades Pitagóricas. Além disso, lembre-se que secante é igual a $latex \frac{1}{\cos(\theta)}$ e cossecante é igual a $latex \frac{1}{\sin(\theta)}$. Usando isso, temos:
$latex {{\tan}^2}(\theta)+1={{\sec}^2}(\theta)=\frac{1}{{{\cos}^2}(\theta)}$
$latex {{\cot}^2}(\theta)+1={{\csc}^2}(\theta)=\frac{1}{{{\sin}^2}(\theta)}$
Substituindo na expressão original, temos:
$latex \frac{1}{{{\sin}^2}(\theta)}+\frac{1}{{{\cos}^2}(\theta)}$
$latex ={{\cot}^2}(\theta)+1+{{\tan}^2}(\theta)+1$
Agora, sabemos que $latex \tan(\theta)=\frac{1}{3}$. Além disso, como cotangente é a função recíproca da tangente, isso significa que $latex \cot(\theta)=3$. Usando esses valores, temos:
$latex {{\cot}^2}(\theta)+1+{{\tan}^2}(\theta)+1$
$latex ={{3}^2}+1+(\frac{1}{3})^2+1$
$latex =\frac{100}{9}$
Veja também
Interessado em aprender mais sobre identidades trigonométricas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
