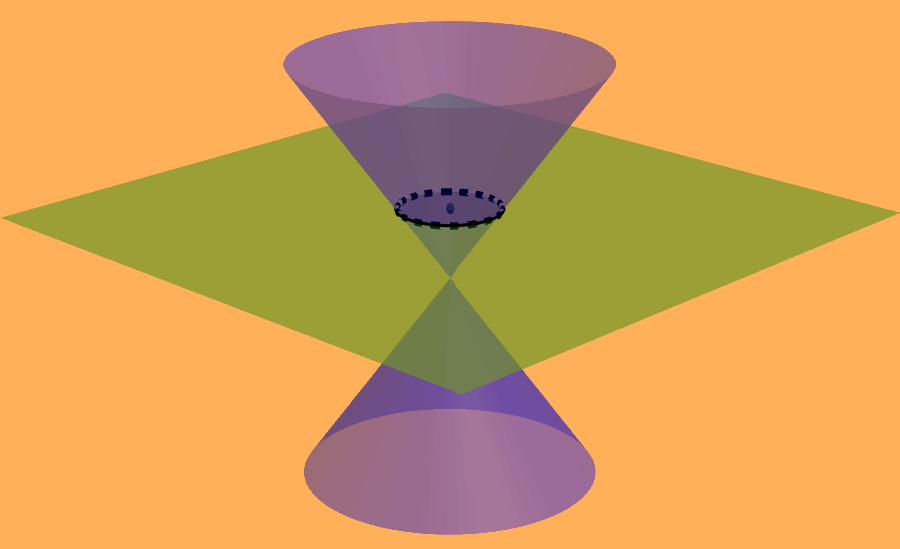
As seções cônicas são obtidas pela interseção da superfície de um cone com um plano. Podemos ter quatro tipos de seções cônicas que são definidas com base no ângulo formado entre o plano e a base do cone. Os quatro tipos de seções cônicas são o círculo, a elipse, a parábola e a hipérbole.
A seguir, aprenderemos mais sobre cada uma das diferentes seções cônicas. Vamos descobrir quais são suas fórmulas e usar diagramas para ilustrá-las. Por fim, revisaremos o conceito de excentricidade, que é uma característica importante das seções cônicas.
O que são seções cônicas?
As seções cônicas são as curvas geradas por um plano que cruza um cone. Os três tipos de seções cônicas são a elipse, a parábola e a hipérbole. O círculo é um tipo de elipse, mas muitas vezes é considerado o quarto tipo de seção cônica.
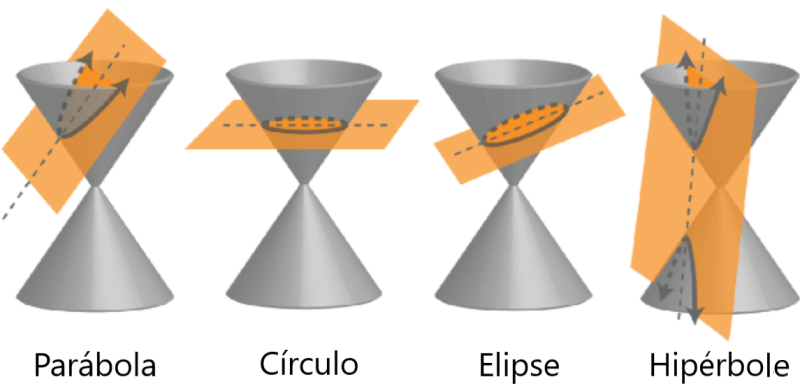
As seções cônicas são geradas pela interseção de um plano com um cone. Se o plano for paralelo ao eixo de revolução (eixo y), a interseção formará uma hipérbole. Se o plano for paralelo a um lado do cone (linha geradora), a interseção formará uma parábola.
Se o plano for perpendicular ao eixo de revolução, a interseção formará um círculo. Se o plano interceptar o cone em um ângulo com o eixo, a interseção formará uma elipse.
Parâmetros de uma seção cônica
A seguir estão alguns dos parâmetros mais importantes definidos em seções cônicas:
Focos: Os focos são dois pontos fixos que definem a seção cônica.
Diretriz: A diretriz é uma linha reta que também define a seção cônica.
Excentricidade: A excentricidade é um parâmetro que determina a forma da seção cônica. Este parâmetro depende do comprimento do semieixo maior e do comprimento do semieixo menor.
Parâmetro focal: O parâmetro focal é a distância do foco até a diretriz correspondente.
Eixo maior: Segmento que une os dois vértices. Em uma elipse, o eixo maior é o maior diâmetro.
Eixo menor: Segmento que une as coberturas. O eixo menor é perpendicular ao eixo maior.
Excentricidade das seções cônicas
A excentricidade é um parâmetro associado a todas as seções cônicas. A excentricidade define a forma da seção cônica e pode ser pensada como uma medida de quanto ela se desvia de ser circular.
A excentricidade é definida por c dividido por a, onde c é o comprimento do centro ao foco e a é o comprimento do centro ao vértice. O valor de e é constante para qualquer seção cônica. Portanto, o valor de e pode ser usado para determinar o tipo de seção cônica:
- Se $latex e=0$, temos um círculo
- Se $latex e\leq 0<1$, temos uma elipse
- Se $latex e=1$, temos uma parábola
- Se $latex e>1$, temos uma hipérbole
Um círculo é definido como um tipo especial de elipse com excentricidade 0. Duas seções cônicas têm a mesma figura somente se sua excentricidade for a mesma.
Seção Cônica – Círculo
Os círculos são formados quando o plano que corta o cone é paralelo à base do cone. A interseção produz um conjunto de pontos que estão à mesma distância de um ponto comum, que é a definição de um círculo.
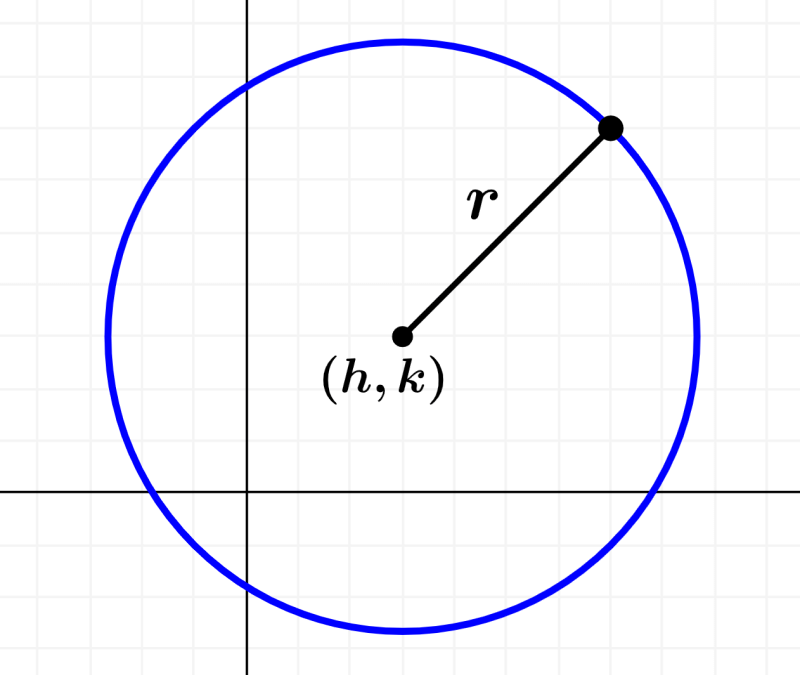
Todos os círculos têm um ponto central, chamado centro, e um raio, que é a distância do centro a qualquer ponto do círculo. Além disso, os círculos têm uma excentricidade de $latex e=0$. No plano cartesiano, a forma geral da equação do círculo é:
| $latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$ |
onde, $latex (h, k)$ é o centro do círculo e r é o raio.
Seção Cônica – Elipse
As elipses são obtidas quando o ângulo do plano em relação ao cone está entre a superfície externa do cone e a base do cone. Esta definição também inclui o caso em que o plano é paralelo à base do cone, de modo que os círculos são um caso especial de elipses.
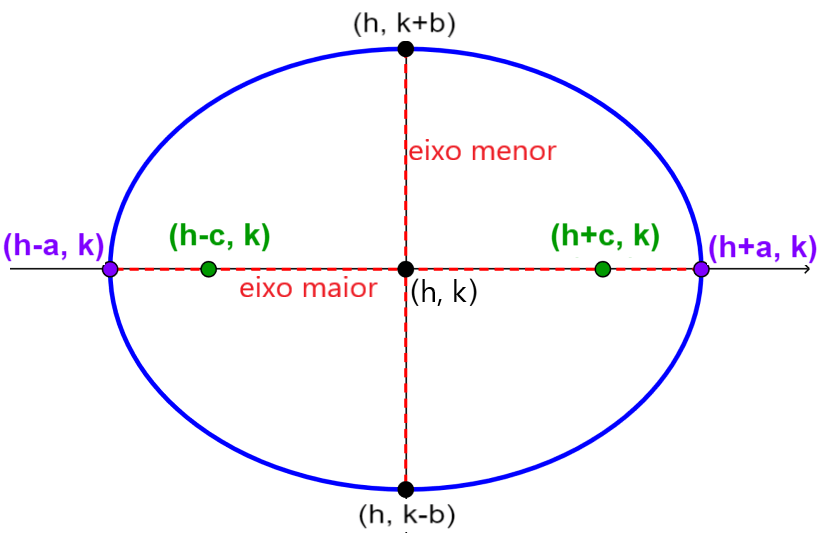
As elipses têm as seguintes características:
- O eixo maior é o maior diâmetro da elipse
- O eixo menor é o menor diâmetro da elipse
- O centro é a intersecção dos dois eixos
- Eles têm dois focos. A soma das distâncias de qualquer ponto da elipse aos dois focos é constante
As elipses podem ter a excentricidade $latex 0\leq e <1$. Vemos que o valor de 0 está incluído (um círculo), mas o 1 não está incluído, pois é a excentricidade de uma parábola. Quando o eixo maior é paralelo ao eixo x, a equação geral de uma elipse é:
| $latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-k)}^2}}{{{b}^2}}=1$ |
onde, $latex (h, k)$ é o centro, 2a é o comprimento do eixo maior e 2b é o comprimento do eixo menor.
Seção Cônica – Parábola
As parábolas são formadas quando o plano é paralelo aos lados do cone. Isso resulta em uma curva em forma de “U”. As parábolas têm as seguintes características:
- O vértice é o ponto onde a curva muda de direção
- O foco é o ponto que está na parte interna da parábola e aquele que dá forma à curva
- A diretriz é a linha que fica do lado de fora da parábola e também a define
- O eixo de simetria é a linha que liga o vértice e o foco e divide a parábola em duas partes iguais
As parábolas têm a excentricidade $latex e=1$. Como todas as parábolas possuem a mesma excentricidade, elas possuem características muito semelhantes e podem ser transformadas com mudança de posição e escala.
As parábolas podem ser representadas por funções quadráticas como:
| $latex f(x)={{x}^2}$ |
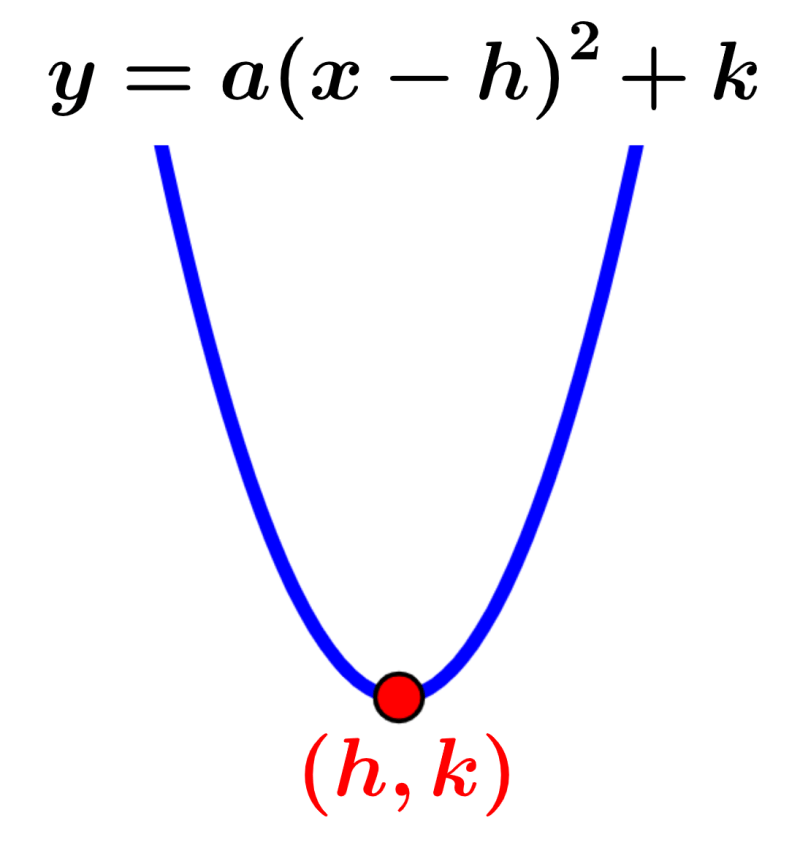
Seção Cônica – Hipérbole
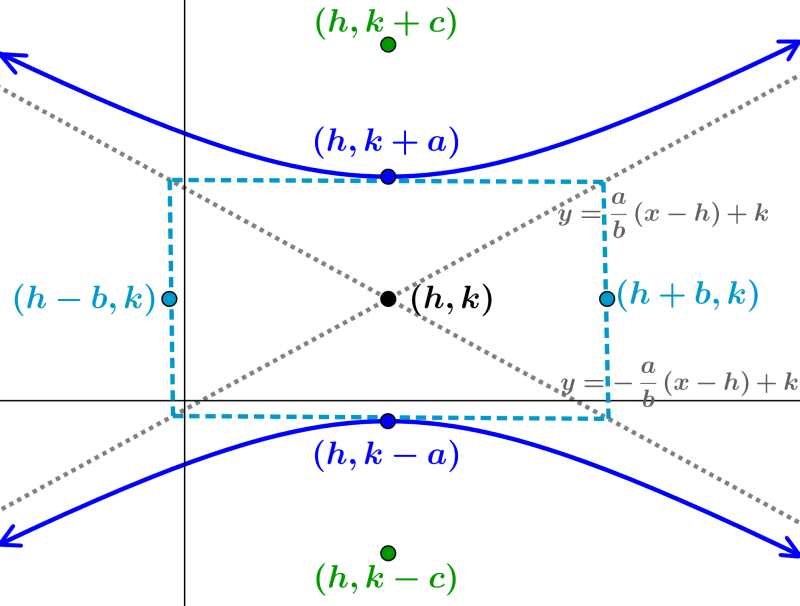
As hipérboles são formadas quando o plano é paralelo ao eixo central do cone. Isso significa que o plano intercepta ambas as bases do cone. As hipérboles são compostas por dois ramos e têm as seguintes características:
- Assíntotas são duas linhas retas que a curva se aproxima, mas nunca toca
- O centro é a intersecção das duas assíntotas
- Os dois focos são os pontos fixos, que definem a forma de cada ramo
- Os dois vértices são os pontos que estão localizados um em cada ramo e onde cada ramo muda de direção
A excentricidade da hipérbole é igual a $latex e>1$. Uma hipérbole que tem os vértices em uma linha horizontal tem a equação geral:
| $latex \frac{{{(x-h}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$ |
onde, $latex (h, k)$ é o centro, 2a é o comprimento do segmento que liga os vértices e 2b é o comprimento do segmento que liga as coberturas.
Fórmulas de seção cônica
A seguir estão as fórmulas para os diferentes tipos de seções cônicas:
Veja também
Interessado em aprender mais sobre seções cônicas? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
