As parábolas são definidas como seções cônicas que são formadas pelo corte de um cone com um plano paralelo a um dos lados do cone. As parábolas são formadas pelo conjunto de todos os pontos equidistantes em relação a uma linha, chamada diretriz, e a um ponto, chamado de foco.
A seguir, aprenderemos como definir uma equação da parábola. Veremos dois casos diferentes: quando o vértice da parábola está localizado na origem e quando o vértice está localizado fora da origem. Aplicaremos o que aprendemos resolvendo alguns exercícios.
Parábolas que têm o vértice em (0, 0)
Uma maneira de definir parábolas é usando a equação geral $latex y = {{x}^2}$. Esta equação representa uma parábola com um vértice na origem (0, 0) e um eixo de simetria em $latex x = 0$.
Além disso, também podemos usar o foco e a diretriz da parábola para obter uma equação, uma vez que cada ponto na parábola é equidistante do foco e da diretriz.
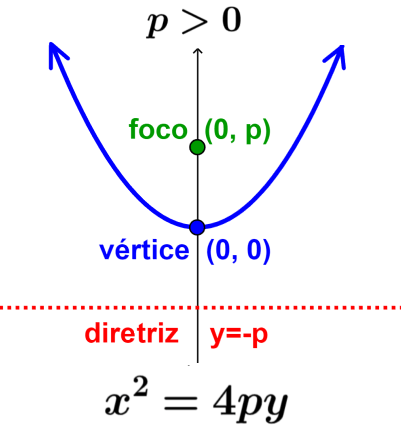
O vértice da parábola está localizado no meio entre o foco e a diretriz. O foco é um ponto localizado no eixo de simetria, enquanto a diretriz é uma linha perpendicular ao eixo de simetria. A imagem a seguir mostra o foco, vértice e diretriz:
Sabemos que podemos descrever uma parábola usando a forma geral $latex y = a {{x}^2}$. É possível reescrever esta equação usando a forma $latex {{x}^2} = 4py$, onde p é uma constante usada para encontrar o foco e a diretriz.
Isso corresponde a uma parábola com orientação vertical. Por outro lado, quando temos uma parábola orientada horizontalmente, temos a equação $latex {{y}^2} = 4px$.
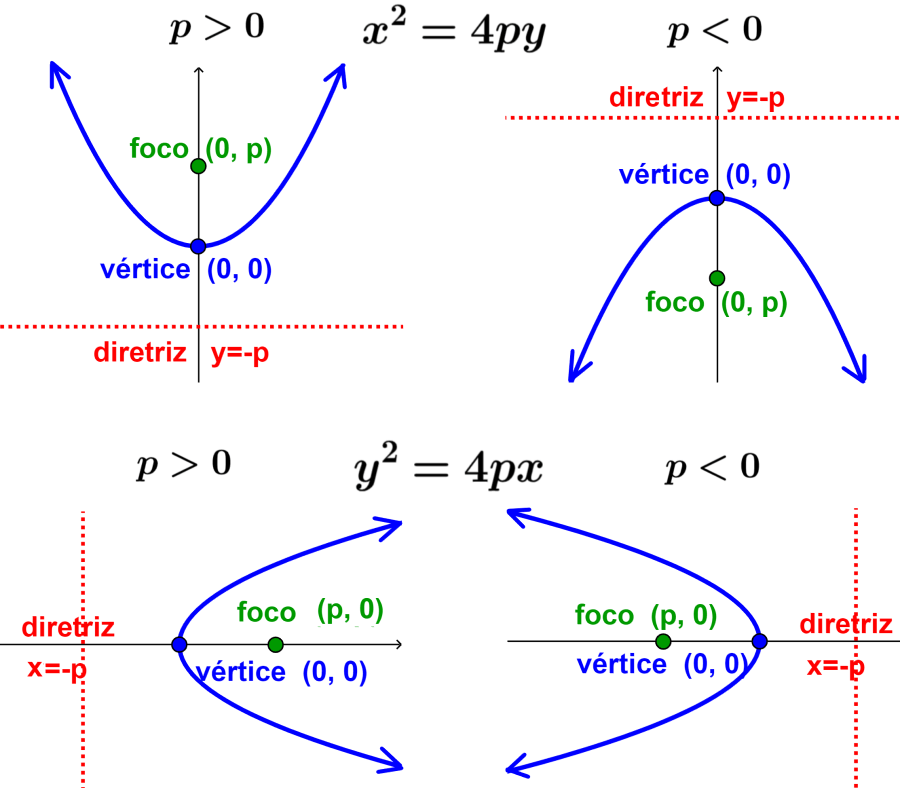
O diagrama mostra os quatro casos diferentes que podemos ter quando a parábola tem um vértice em (0, 0). Quando a variável x é quadrada, a parábola é orientada verticalmente e quando a variável y é quadrada, a parábola é orientada horizontalmente.
Além disso, quando o valor de p é positivo, a parábola se abre para a parte positiva dos eixos, ou seja, para cima ou para a direita.
Por outro lado, quando o valor de p é negativo, a parábola se abre para a parte negativa dos eixos, ou seja, para baixo ou para a esquerda.
EXEMPLO 1
Qual é a equação de uma parábola que tem foco em (0, 3)?
Solução
Sabemos que o vértice da parábola está localizado em (0, 0). O fato de o foco estar em (0, 3) indica que o valor de p é o valor de y e é positivo. Isso significa que a parábola se abrirá para cima. Portanto, a equação geral é $latex {{x}^2}=4py$.
Substituindo p por 3, temos:
$latex {{x}^2}=4(3)y$
$latex {{x}^2}=12y$
EXEMPLO 2
Se tivermos a parábola $latex y = \frac{1}{2} {{x}^2}$, qual é o seu foco e diretriz?
Solução
Encontramos o foco e a diretriz resolvendo $latex {{x}^2}$ e determinando o valor de p . Então, temos:
$latex y=\frac{1}{2}{{x}^2}$
$latex 2y={{x}^2}$
Podemos formar a equação $latex 2 = 4p$ e resolver para p:
$latex 2=4p$
$latex p=\frac{1}{2}$
Então, o foco é $latex (0, \frac{1}{2})$ e a diretriz é $latex y=-\frac{1}{2}$.
Parábolas que têm o vértice em (h, k)
Nem todas as parábolas têm seu vértice no ponto (0, 0), pois em muitos casos, as parábolas têm seu vértice no ponto $latex (h, k)$ que está localizado fora da origem.
Acima vimos que, quando o vértice da parábola está localizado na origem, sua equação é $latex {{x}^2} = 4py$ ou $latex {{y}^2} = 4px$ dependendo de sua orientação.
Se combinarmos essas equações com a forma do vértice das parábolas, $latex y = a{{(x-h)}^2} -k$, podemos formar uma equação que se aplica aos casos em que o vértice não está na origem.
Então, começamos isolando $latex {{(x-h)}^2}$:
$latex y=a{{(x-h)}^2}-k$
$latex {{(x-h)}^2}=\frac{1}{a}(y-k)$
Se compararmos esta equação com $latex {{x}^2}=4py$, temos $latex 4p=\frac{1}{a}$. Então:
$latex {{(x-h)}^2}=4p(y-k)$
Esta é a equação de uma parábola orientada verticalmente. Por outro lado, se a parábola for orientada horizontalmente, sua equação será $latex {{(y-k)}^2}=4p(x-h)$.
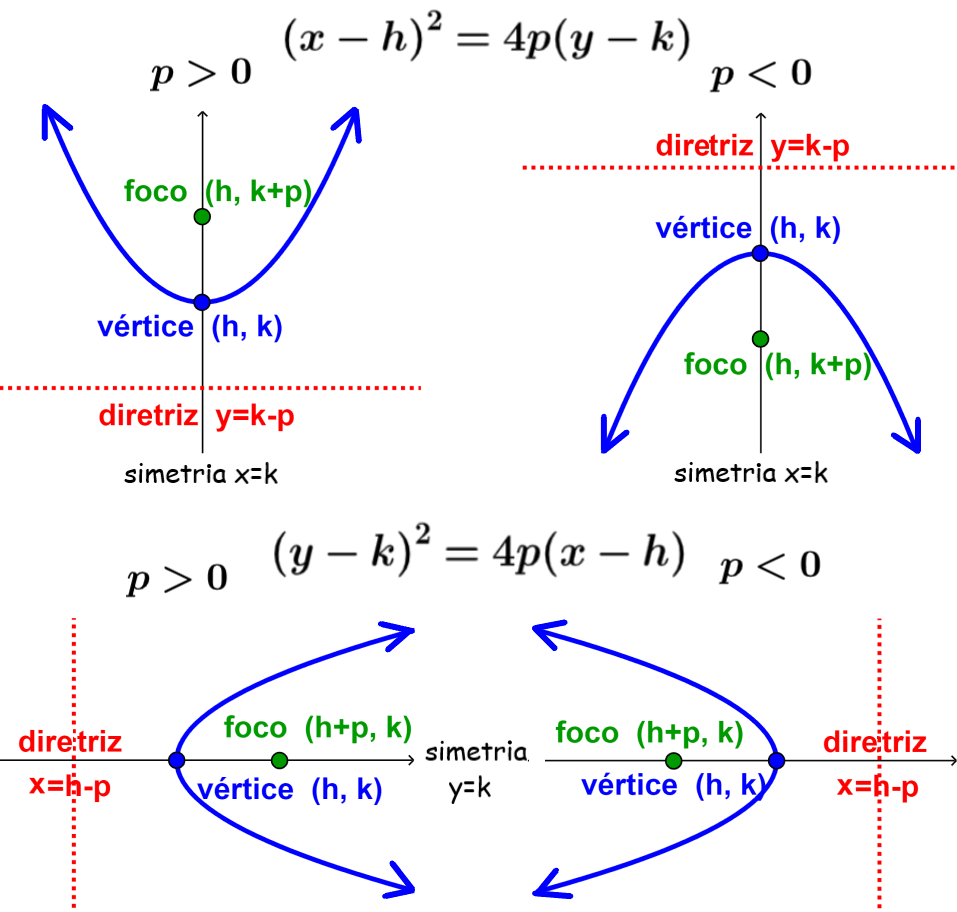
O diagrama nos mostra que quando a variável x é ao quadrado, a parábola é orientada verticalmente e quando a variável y é ao quadrado, a parábola é orientada horizontalmente.
Além disso, o valor de p indica onde a parábola se abre. Se p for positivo, a parábola se abre para a parte positiva dos eixos. Se p for negativo, a parábola se abre para a parte negativa dos eixos.
EXEMPLO 1
Se o vértice de uma parábola está localizado em (-2, 4) e sua diretriz é $latex y = 7$, qual é sua equação?
Solução
Vemos que a diretriz é uma linha horizontal, então a parábola é orientada verticalmente e abrirá para cima ou para baixo. Além disso, também vemos que a diretriz está localizada acima do vértice, então a parábola abre para baixo e o valor de p é negativo.
Podemos encontrar o valor de p usando o vértice $latex (h, k)$. A equação para uma diretriz horizontal é $latex y = k-p$. Então, temos:
$latex 7=4-p$
$latex 3=-p$
$latex p=-3$
Usando esses valores, temos:
$latex {{(x-h)}^2}=4p(y-k)$
$latex {{(x-(-2))}^2}=4(-3)(y-4)$
$latex {{(x+2)}^2}=-12(y-4)$
EXEMPLO 2
Qual é o vértice, foco, eixo de simetria e diretriz da parábola $latex {{(x + 3)}^2} = 4 (y + 4)$?
Solução
Podemos comparar esta equação com a equação geral dada acima. Portanto, o vértice é o ponto $latex (-3, -4)$. Além disso, como a variável x é ao quadrado, a parábola se abre para cima.
Agora, formamos a equação $latex 4p=4$. Resolvendo para p, temos $latex p=1$. Isso significa que o foco é $latex (-3, -4+1)=(-3, -3)$, o eixo de simetria é $latex x=-3$ e a diretriz é $latex y=-3-1=-4$.
Veja também
Você quer aprender mais sobre equações de parábolas? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
