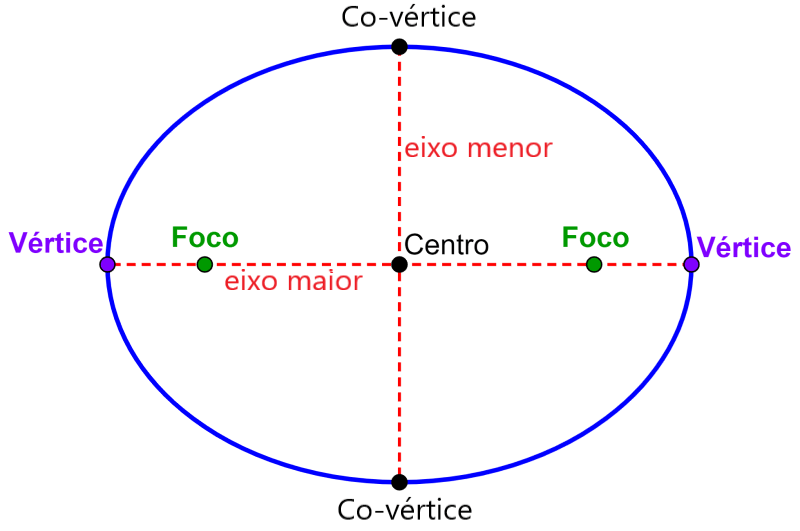
As elipses são formadas pelo conjunto de todos os pontos que possuem distâncias de dois pontos fixos que, quando somados, são iguais a um valor constante. Os pontos fixos são chamados de focos da elipse. As elipses têm duas linhas de simetrias. O eixo com o comprimento mais longo é denominado eixo maior e o eixo com o comprimento mais curto é denominado eixo menor. Os vértices da elipse são os pontos finais do eixo maior e os co-vértices são os pontos finais do eixo menor. O centro de uma elipse é o ponto de intersecção do eixo maior e do eixo menor. Os focos estão sempre localizadas no eixo maior.
A seguir, conheceremos a equação da elipse que tem um centro fora da origem. Veremos equações para elipses orientadas verticalmente e elipses orientadas horizontalmente.
Forma padrão de elipses centradas fora da origem
Muitas vezes, as elipses não são centralizadas na origem, portanto, não podemos usar as equações mais básicas que usamos quando temos um centro na origem. No entanto, semelhante a outros gráficos, os gráficos de elipse podem ser transladada horizontalmente e verticalmente. Se uma elipse é transladada h unidades horizontalmente e k unidades verticalmente, seu centro estará em (h, k). Podemos usar esse movimento na equação padrão de uma elipse, substituindo x por (x-h) e y por (y-k).
Além de ter elipses centradas na origem e fora da origem, também temos elipses com orientação vertical ou horizontal.
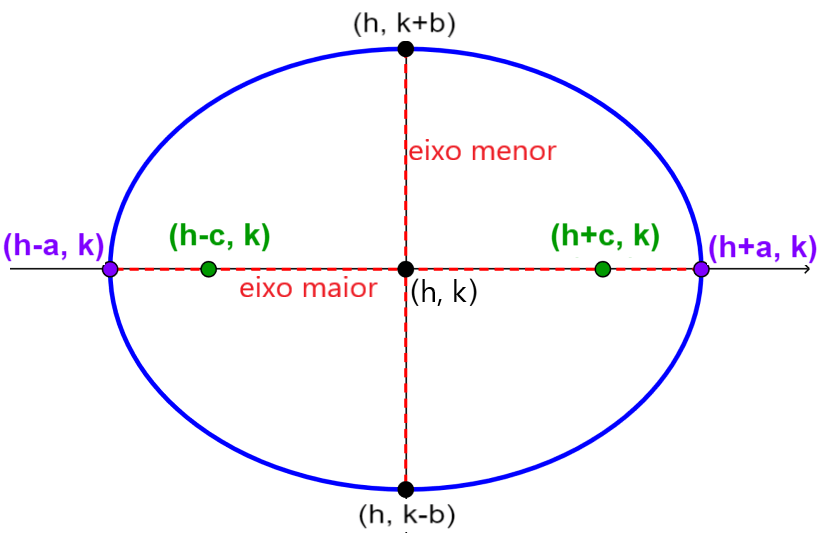
Equação da elipse horizontal centrada fora da origem
A forma padrão de uma elipse centrada em ( h, k ) e com o eixo maior paralelo ao eixo x é:
| $latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-h)}^2}}{{{b}^2}}=1$ |
onde,
- $latex a>b$
- O eixo maior é $latex 2a$
- O eixo menor é $latex 2b$
- Os vértices estão localizados em $latex (h\pm a, k)$
- Os co-vértices estão localizados em $latex (h, k\pm b)$
- Os focos estão localizados em $latex (h \pm c, k)$, onde, $latex {{c}^2}={{a}^2}-{{b}^2}$
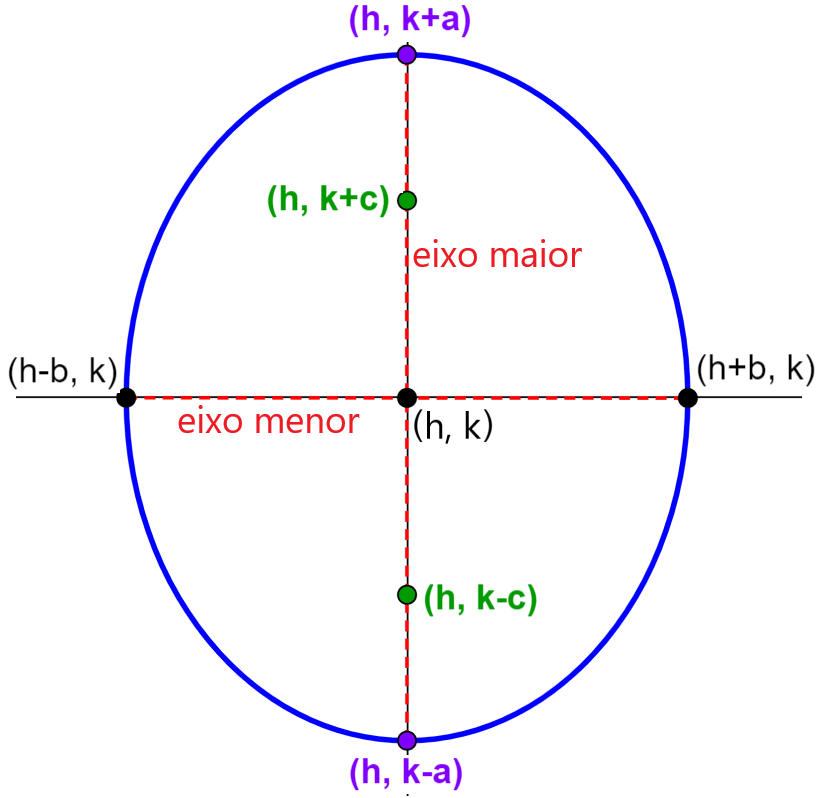
Equação da elipse vertical centrada fora da origem
A equação de uma elipse em sua forma padrão que tem seu centro em ( h, k ) e em que seu eixo maior é paralelo ao eixo y é:
| $latex \frac{{{(x-h)}^2}}{{{b}^2}}+\frac{{{(y-k)}^2}}{{{a}^2}}=1$ |
onde,
- $latex a>b$
- O comprimento do eixo maior é $latex 2a$
- O comprimento do eixo menor é $latex 2b$
- Os vértices estão localizados em $latex (h, k\pm a)$
- Os co-vértices estão localizados em $latex (h\pm b, k)$
- Os focos estão localizados em $latex (h, k\pm c)$, onde, $latex {{c}^2}={{a}^2}-{{b}^2}$
Escrever a equação para elipses centradas fora da origem usando vértices e focos
Usamos os seguintes passos para determinar a equação de uma elipse centrada fora da origem se conhecermos os vértices e focos:
Passo 1: Determinamos se o eixo maior é paralelo ao eixo x ou ao eixo y.
1.1. Se as coordenadas y dos vértices forem iguais às coordenadas y dos focos, o eixo maior é paralelo ao eixo x e usamos a equação $latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-k)}^2}}{{{b}^2}}=1$.
1.2. Se as coordenadas x dos vértices forem iguais às coordenadas y dos focos, o eixo maior é paralelo ao eixo y e usamos a equação $latex \frac{{{(x-h)}^2}}{{{b}^2}}+\frac{{{(y-k)}^2}}{{{a}^2}}=1$.
Passo 2: Podemos determinar as coordenadas do centro da elipse ( h, k ) usando as coordenadas dos vértices e reconhecendo que o centro está no ponto médio.
Passo 3: Encontramos o valor de $latex {{a}^2}$ encontrando o comprimento do eixo maior, 2a. Este comprimento é a distância entre os dois vértices.
Passo 4: Encontramos o valor de $latex {{c}^2}$ usando os valores de h e k junto com as coordenadas dos focos.
Passo 5: Resolvemos para $latex {{b}^2}$ usando a equação $latex {{c}^2}={{a}^2}-{{b}^2}$.
Passo 6: Substituímos os valores de $latex {{a}^2}$, $latex {{b}^2}$, h e k na equação obtida no passo 1.
Exercícios resolvidos de equação da elipse com centro fora da origem
O que foi aprendido sobre as equações de elipses que têm o centro no ponto (h, k) é aplicado para resolver os exercícios a seguir. Analise o processo usado com cuidado.
EXERCÍCIO 1
Encontre a equação da elipse que possui vértices em (-1, -9) e (-1, 3) e focos em (-1, -8) e (-1, 2).
Solução
Vemos que as coordenadas x dos vértices e dos focos são as mesmas, então o eixo maior é paralelo ao eixo y . Assim, a equação da elipse terá a seguinte forma:
$latex \frac{{{(x-h)}^2}}{{{b}^2}}+\frac{{{(y-k)}^2}}{{{a}^2}}=1$
Para encontrar o centro, usamos a fórmula do ponto médio, pois o centro está entre os vértices $latex (-1, -9)$ e $latex (-1, 3)$. Então, temos:
$latex (h, k)=(\frac{-1+(-1)}{2}, \frac{-9+3}{2})$
$latex =(-1, -3)$
Agora, vamos encontrar $latex {{a}^2}$. O comprimento do eixo maior, $latex 2a$, é limitado pelos dois vértices. Portanto, a distância entre os vértices é:
$latex 2a=3-(-9)$
$latex 2a=12$
$latex a=6$
Então, temos $latex {{a}^2}=36$.
Agora, encontramos $latex {{c}^2}$. Para elipses verticais, os focos são dados por $latex (h, k \pm c)$. Portanto, temos $latex (h, k-c) = (- 1, -8)$ e $latex (h, k + c) = (- 1,2)$. Usamos o valor $latex k = -3$ em qualquer um desses pontos e resolvemos:
$latex k+c=2$
$latex -3+c=2$
$latex c=5$
Então, temos $latex {{c}^2}=25$.
Agora, usamos a equação $latex {{c}^2} = {{a}^2} – {{b}^2}$ para obter o valor de $latex {{b}^2}$. Então, temos:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex 25=36-{{b}^2}$
$latex {{b}^2}=11$
Finalmente, usamos os valores obtidos na equação da elipse:
$latex \frac{{{(x+1)}^2}}{11}+\frac{{{(y+3)}^2}}{36}=1$
EXERCÍCIO 2
Qual é a equação da elipse que tem vértices em (-4, 2), (8, 2) e focos em (-2, 2), (6, 2)?
Solução
Neste caso, as coordenadas y dos vértices e focos são as mesmas. Isso significa que o eixo maior é paralelo ao eixo x . Portanto, a equação da elipse terá a seguinte forma:
$latex \frac{{{(x-h)}^2}}{{{a}^2}}+\frac{{{(y-k)}^2}}{{{b}^2}}=1$
Encontramos o centro usando a fórmula do ponto médio, pois o centro está entre os vértices $latex (-4, 2)$ e $latex (8, 2)$. Então, temos:
$latex (h, k)=(\frac{-4+8}{2}, \frac{2+2}{2})$
$latex =(2, 2)$
Encontramos $latex {{a}^2}$ usando o comprimento do eixo maior, $latex 2a$. Este comprimento é igual à distância entre os vértices. Então, temos:
$latex 2a=8-(4)$
$latex 2a=12$
$latex a=6$
Então, temos $latex {{a}^2}=36$.
Vamos encontrar $latex {{c}^2}$. Em uma elipse horizontal, os focos são dados por $latex (h \pm c, k)$. Portanto, temos $latex (h-c, k) = (- 2, 2)$ e $latex (h + c, k) = (6,2)$. Usamos qualquer um desses pontos com o valor $latex h = 2$ e resolvemos:
$latex h+c=6$
$latex 2+c=6$
$latex c=4$
Então, temos $latex {{c}^2}=16$.
Encontramos o valor de $latex {{b}^2}$ usando a equação $latex {{c}^2}={{a}^2}-{{b}^2}$. Então, temos:
$latex {{c}^2}={{a}^2}-{{b}^2}$
$latex 16=36-{{b}^2}$
$latex {{b}^2}=20$
Finalmente, usamos os valores obtidos na equação da elipse:
$latex \frac{{{(x-2)}^2}}{36}+\frac{{{(y-2)}^2}}{20}=1$
Exercícios de equação da elipse com centro fora da origem para resolver
Use o que você aprendeu sobre equações para elipses com centro fora da origem para resolver os exercícios a seguir. Veja os exercícios resolvidos acima caso precise de ajuda com isso.
Veja também
Você quer aprender mais sobre equações de elipses? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
