As hipérboles são definidas como seções cônicas que são obtidas quando um cone duplo é interceptado por um plano. A hipérbole é formada quando o plano cruza as duas faces do cone. A hipérbole contém dois ramos em forma de parábola e que são reflexos um do outro. O conjunto de todos os pontos de uma hipérbole são caracterizados pelo fato de que a diferença das distâncias entre qualquer ponto da hipérbole e os focos é igual a uma constante.
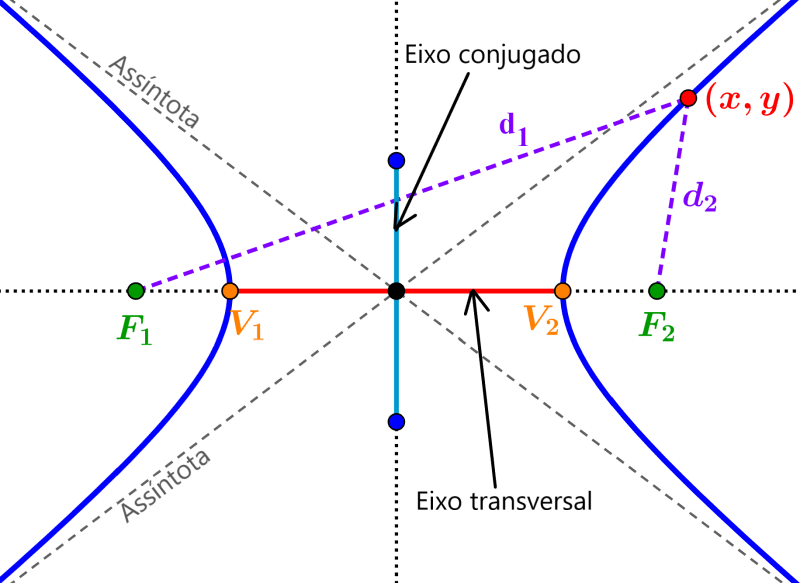
Uma hipérbole tem duas linhas de simetria. O eixo transversal se estende de um vértice ao outro e passa pelo centro. Os focos definem a hipérbole e estão localizados na linha que contém o eixo transversal. O eixo conjugado se estende de um co-vértice ao outro e é perpendicular ao eixo transversal. O ponto de intersecção do eixo transversal e do eixo conjugado é o centro da hipérbole. O centro também é o ponto de intersecção das duas assíntotas.
Forma padrão de hipérboles centradas fora da origem
A forma padrão de hipérboles centradas fora da origem é encontrada aplicando uma translação de h unidades no eixo x e k unidades no eixo y. Isso resulta no centro da hipérbole sendo localizado em $latex (h, k)$. Temos duas variações desta equação dependendo da orientação da hipérbole.
Equação da hipérbole horizontal com centro fora da origem
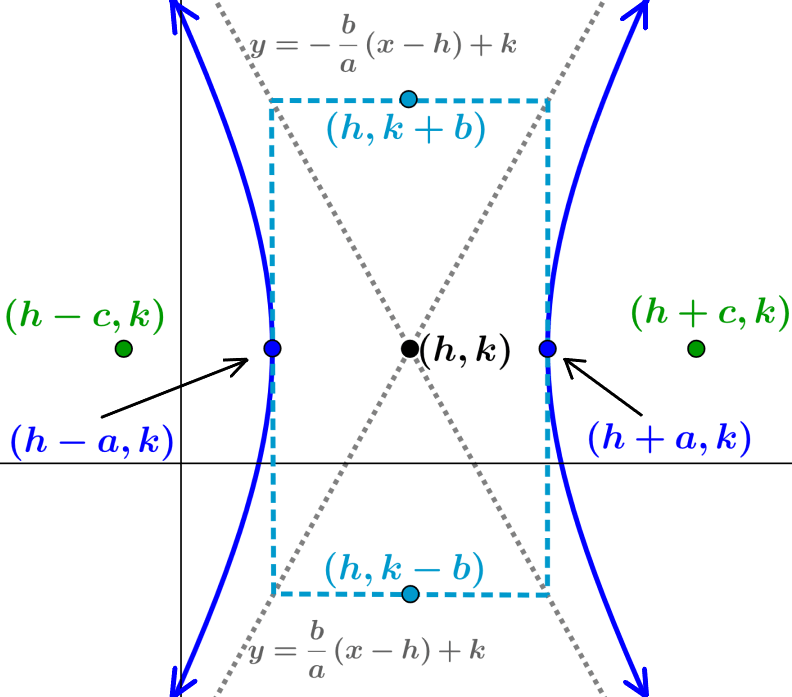
Uma hipérbole que tem seu centro em $latex (h, k)$ e em que seu eixo transversal é paralelo ao eixo x é:
| $latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$ |
onde,
- h é a coordenada em x do centro e k é a coordenada y do centro
- O comprimento do eixo transversal é $latex 2a$ (segmento que une os vértices)
- Os vértices estão localizados em $latex (h\pm a, k)$
- O comprimento do eixo conjugado é $latex 2b$ (segmento que une os co-vértices)
- Os co-vértices estão localizados em $latex (h, k\pm b)$
- A distância entre os focos é $latex 2c$
- Encontramos c usando $latex {{c}^2}={{a}^2}+{{b}^2}$
- Os focos estão localizados em $latex (h \pm c, 0)$
- As equações das assíntotas são $latex y=\pm \frac{b}{a}(x-h)+k$
Equação da hipérbole vertical com centro fora da origem
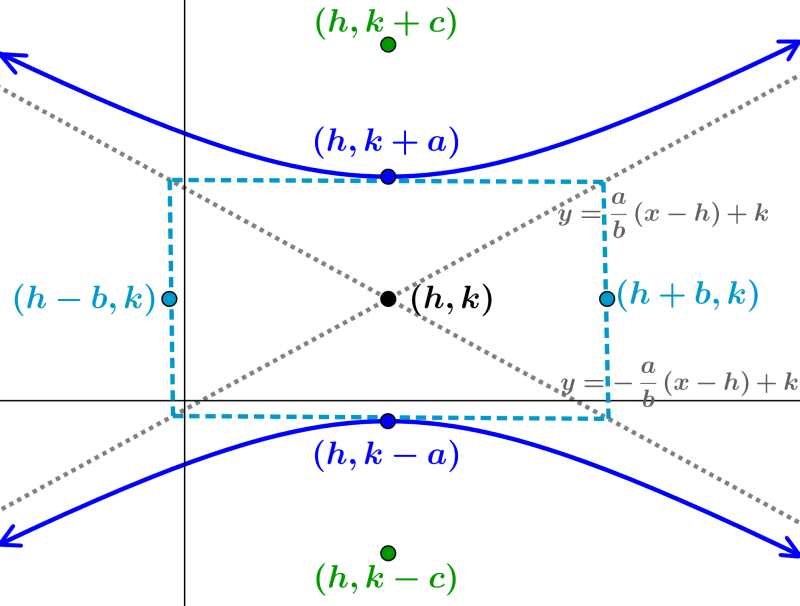
Quando a hipérbole está centrada no ponto $latex (h, k)$ e seu eixo transversal é paralelo ao eixo y , sua equação é:
| $latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$ |
onde,
- h é a coordenada em x do centro e k é a coordenada y do centro
- O comprimento do eixo transversal é $latex 2a$ (segmento que une os vértices)
- Os vértices têm as coordenadas $latex (h, k\pm a)$
- O comprimento do eixo conjugado é $latex 2b$ (segmento que une os co-vértices)
- Os co-vértices têm as coordenadas $latex (h\pm b, k)$
- A distância entre os focos é $latex 2c$, onde, $latex {{c}^2}={{a}^2}+{{b}^2}$
- Os focos têm as coordenadas $latex (h, k\pm c)$
- As assíntotas têm as equações $latex y=\pm \frac{a}{b}(x-h)+k$
Determinar a equação das hipérboles fora da origem usando vértices e focos
Podemos usar as coordenadas dos vértices e focos para encontrar a equação de uma hipérbole centrada fora da origem seguindo estos passos:
Passo 1: Determine a orientação da hipérbole. Temos que determinar se o eixo transversal é paralelo ao eixo x ou paralelo ao eixo y.
1.1. Quando as coordenadas y dos vértices são iguais às coordenadas y dos focos, o eixo transversal é paralelo ao eixo x e usamos a equação $latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$.
1.2. Quando as coordenadas x dos vértices são iguais às coordenadas x dos focos, o eixo transversal é paralelo ao eixo y e usamos a equação $latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$.
Passo 2: Usamos as coordenadas dos vértices e a fórmula do ponto médio para encontrar o centro $latex (h, k)$.
Passo 3: A distância entre os vértices é $latex 2a$. Usamos isso para encontrar $latex {{a}^2}$.
Passo 4: Usamos as coordenadas dos focos e os valores de h e k para encontrar o valor de c e $latex {{c}^2}$.
Passo 5: Usamos a equação $latex {{b}^2}={{c}^2}-{{a}^2}$ para encontrar o valor de $latex {{b}^2}$.
Passo 6:Substituímos os valores de $latex a^2$ e $latex {{b}^2}$ na equação obtida no passo 1.
Exercícios resolvidos de equações de hipérboles com centro fora da origem
Os exercícios a seguir aplicam o que você aprendeu sobre as equações da hipérbole. Vértices e focos são usados para determinar as equações. Analise os exercícios para conhecer o processo utilizado.
EXERCÍCIO 1
Qual é a equação da hipérbole que possui vértices em (-1, 1), (3, 1) e focos em (-2, 1), (4, 1)?
Solução
As coordenadas y dos focos e dos vértices são iguais, portanto sabemos que o eixo transversal é paralelo ao eixo x e a equação da hipérbole tem a forma:
$latex \frac{{{(x-h)}^2}}{{{a}^2}}-\frac{{{(y-k)}^2}}{{{b}^2}}=1$
Para encontrar o centro, observamos que o centro está no meio dos vértices (-1, 1) e (3, 1). Então, aplicamos a fórmula do ponto médio:
$latex (h, k)=(\frac{-1+3}{2}, \frac{1+1}{2})$
$latex =(1, 1)$
Para encontrar $latex {{a}^2}$, determinamos o comprimento do eixo transversal, 2a , que é limitado pelos vértices. Então, encontramos a diferença nas coordenadas x dos vértices:
$latex 2a=|3-1|$
$latex 2a=2$
$latex a=2$
$latex {{a}^2}=4$
Agora, encontramos $latex {{c}^2}$. As coordenadas dos focos são $latex (h \pm c, k)$. Portanto, temos $latex (h-c, k) = (- 2, 1)$ e $latex (h + c, k) = (4, 1)$. Podemos usar qualquer um desses pontos para encontrar o valor de c:
$latex h+c=4$
$latex 1+c=4$
$latex c=3$
$latex {{c}^2}=9$
Agora, usamos a equação $latex {{b}^2}={{c}^2}-{{a}^2}$ para encontrar o valor de $latex {{b}^2}$:
$latex {{b}^2}={{c}^2}-{{a}^2}$
$latex =9-4$
$latex =5$
Substituindo os valores de h, k, $latex {{a}^2}$ e $latex {{b}^2}$, temos:
$latex \frac{{{(x-1)}^2}}{4}-\frac{{{(y-1)}^2}}{5}=1$
EXERCÍCIO 2
Se uma hipérbole tem focos em (2, 0), (2, 6) e vértices em (2, 1), (2, 5), qual é a sua equação?
Solução
Neste caso, vemos que as coordenadas x dos focos e dos vértices são as mesmas. Isso significa que o eixo transversal é paralelo ao eixo y e a equação da hipérbole tem a forma:
$latex \frac{{{(y-k)}^2}}{{{a}^2}}-\frac{{{(x-h)}^2}}{{{b}^2}}=1$
Usamos os vértices (2, 1) e (2, 5) junto com a fórmula do ponto médio para encontrar o centro:
$latex (h, k)=(\frac{2+2}{2}, \frac{1+5}{2})$
$latex =(2, 3)$
Agora, encontramos o comprimento do eixo transversal, 2a. Então, encontramos a diferença nas coordenadas y dos vértices:
$latex 2a=|5-1|$
$latex 2a=4$
$latex a=2$
$latex {{a}^2}=4$
Usamos as coordenadas dos focos, $latex (h, k\pm c)$, para encontrar o valor de $latex {{c}^2}$. Então, temos $latex (h, k-c)=(2, 0)$ e $latex (h, k+c)=(2, 6)$. Podemos usar qualquer um desses pontos para encontrar o valor de c:
$latex k+c=6$
$latex 3+c=6$
$latex c=3$
$latex {{c}^2}=9$
Agora, usamos a equação $latex {{b}^2}={{c}^2}-{{a}^2}$ para encontrar o valor de $latex {{b}^2}$:
$latex {{b}^2}={{c}^2}-{{a}^2}$
$latex =9-4$
$latex =5$
Substituindo os valores de h, k, $latex {{a}^2}$ e $latex {{b}^2}$, temos:
$latex \frac{{{(y-3)}^2}}{4}-\frac{{{(y-2)}^2}}{5}=1$
Exercícios de equações de hipérboles com centro fora da origem para resolver
Aplique os métodos e passos vistos acima para resolver os exercícios a seguir e encontrar as equações das hipérboles usando as coordenadas dos vértices e dos focos.
Veja também
Você quer aprender mais sobre equações de hipérbole? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
