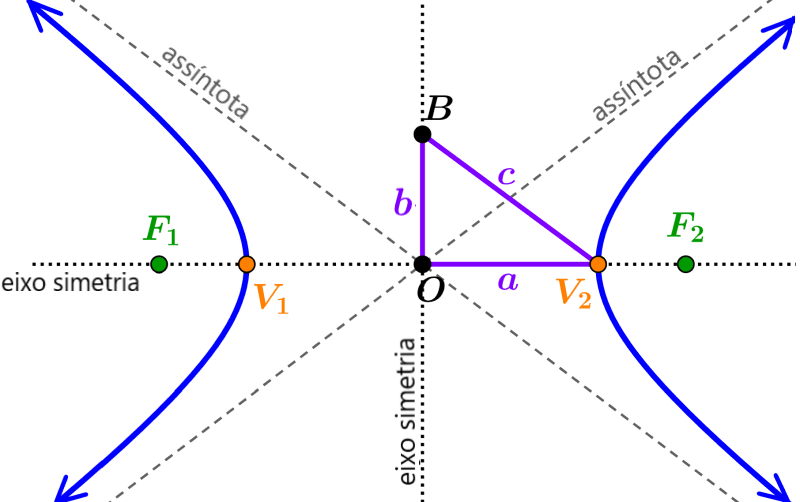
As hipérboles consistem em duas peças com formato semelhante a parábolas. Uma peça se abre para cima e a outra para baixo ou uma para a esquerda e a outra para a direita. Além disso, semelhante às parábolas, cada uma das peças tem um vértice. Os gráficos das hipérboles também possuem duas linhas, chamadas assíntotas. As assíntotas não são oficialmente parte das hipérboles, mas são incluídas para garantir que obtenhamos o gráfico correto. Os elementos mais importantes de uma hipérbole são os focos, vértices, eixos, distância focal, semi-eixos e assíntotas.
A seguir, conheceremos mais detalhes desses elementos junto com os diagramas.
Definição de uma hipérbole
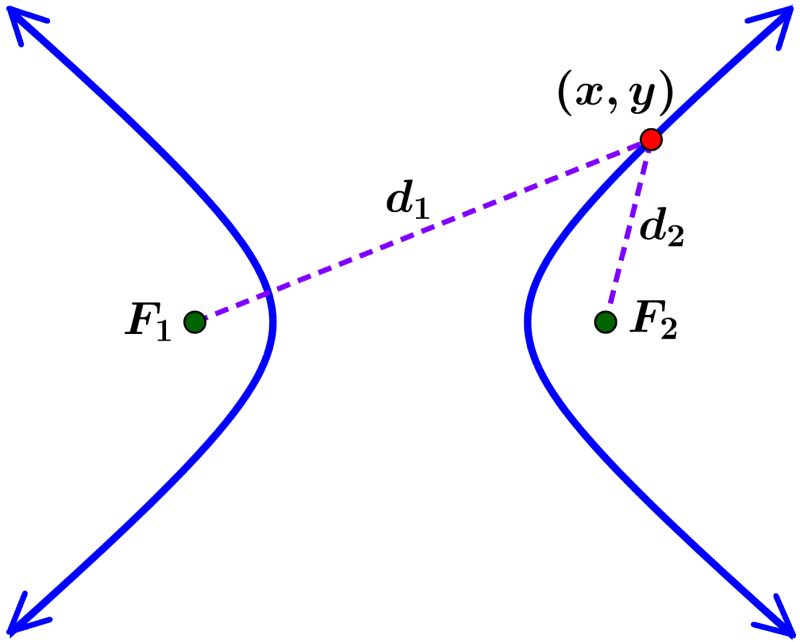
Uma hipérbole é o conjunto de todos os pontos, que possuem distâncias de dois pontos fixos, chamados focos, que tem uma diferença igual a uma constante. Por exemplo, se os pontos $latex F_{1}$ e $latex F_{2}$ são os focos e d é uma constante, então o ponto $latex (x, y)$ é parte da hipérbole se $latex d = | d_{1} – d_{2} |$ conforme mostrado na seguinte imagem:
Também podemos definir hipérboles como as seções cônicas que são formadas pela interseção de dois cones com um plano inclinado que intercepta a base dos cones. As hipérboles consistem em duas curvas separadas, chamadas ramos.
Os pontos em que a distância é o mínimo entre os dois ramos são chamados de vértices. O ponto médio dos vértices da hipérbole é o centro. Uma hipérbole é assintótica em relação a certas linhas traçadas pelo centro.
Elementos fundamentais de uma hipérbole
A seguir estão os elementos fundamentais de uma hipérbole:
- Focos
- Eixo transversal
- Eixo conjugado
- Semi-eixo maior
- Semi-eixo menor
- Centro
- Vértices
- Comprimento focal
- Eixos de simetria
- Assíntotas
Focos
Os focos são os pontos fixos usados para definir a hipérbole. Os focos são frequentemente definidos por $latex F_{1}$ e $latex F_{2}$ ou também por $latex F$ e $latex F’$.
As coordenadas dos focos são dadas por $latex F = (h \pm c, k)$ se o eixo transversal for paralelo ao eixo x e por $latex F = (h, k \pm c)$ se o eixo transversal for paralelo ao eixo y. O ponto $latex (h, k)$ é o centro e encontramos c usando $latex {{c}^2} = {{a}^2} + {{b}^2}$.
Eixo transversal
O eixo transversal, também conhecido como eixo real, é o segmento que passa entre os dois focos. O eixo transversal pode ser determinado usando a equação da hipérbole. Sabemos que a equação da hipérbole contém um termo negativo e um termo positivo.
Se o sinal positivo estiver no termo x, significa que o eixo transversal está no eixo x e se o sinal positivo estiver no termo y, significa que o eixo transversal está no eixo y.
Eixo conjugado
O eixo conjugado, também conhecido como eixo imaginário, é a bissetriz perpendicular do eixo transversal. O eixo conjugado divide o eixo transversal em duas partes iguais.
Semi-eixo maior
O semi-eixo maior é o segmento que se estende do centro até um vértice da hipérbole. Seu comprimento é denotado por a.
Semi-eixo menor
O semi-eixo menor é o segmento perpendicular ao semi-eixo maior. Seu comprimento é denotado por b.
Centro
O centro possui duas linhas de simetria. O centro é o ponto de intersecção das duas linhas de simetria. Se a hipérbole estiver centrada na origem, o centro é (0,0) e se estiver centrado em outro ponto, o centro é $latex (h, k)$.
Vértices
Os vértices são os pontos de intersecção da hipérbole com o eixo transversal. Os vértices são os pontos finais de cada ramificação da hipérbole. Normalmente, usamos $latex V_{1}$ e $latex V_{2}$ ou $latex V$ e $latex V’$ para representar os vértices.
Comprimento focal
O comprimento focal é o comprimento do segmento que se estende de um foco $latex (F_{1})$ para o outro foco $latex (F_{2})$. Seu comprimento é igual a 2c.
Eixos de simetria
As linhas de simetria são os eixos que coincidem com o eixo transversal e o eixo conjugado. Os dois ramos da hipérbole são simétricos. As hipérboles têm duas linhas de simetria, o eixo horizontal e o eixo vertical. O ponto de intersecção desses eixos é o centro.
Assíntotas
As assíntotas são as linhas que ficam muito próximas às ramificações da hipérbole, mas nunca as tocam. As assíntotas se cruzam no centro da hipérbole.
Veja também
Você quer aprender mais sobre equações de hipérbole? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
