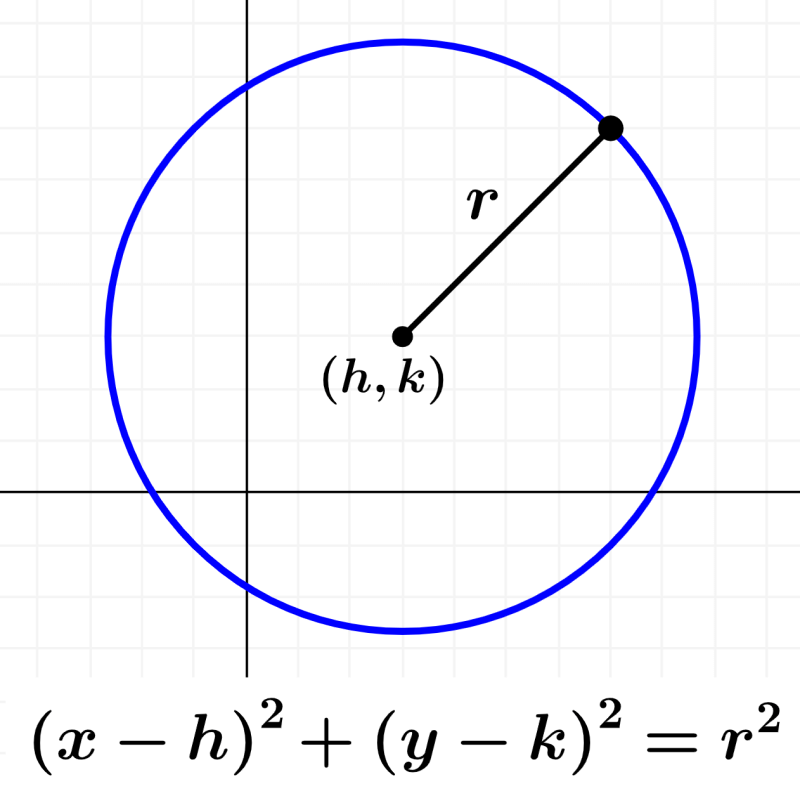As circunferências são formadas por um conjunto de pontos que estão localizados à mesma distância de um ponto fixo. O ponto fixo é chamado de centro da circunferência e a distância entre os pontos é chamada de raio. A equação de uma circunferência com centro fora da origem é encontrada usando a equação de uma circunferência que tem um centro na origem e então aplicamos as translações vertical e horizontal.
A seguir, aprenderemos a encontrar equações para esses tipos de circunferências. Em seguida, veremos alguns exercícios práticos.
PRÉ-CÁLCULO
Relevante para…
Aplicar a equação da circunferência com centro fora da origem.
PRÉ-CÁLCULO
Relevante para…
Aplicar a equação da circunferência com centro fora da origem.
Circunferências com centros fora da origem
Para encontrar a equação de uma circunferência centrada fora da origem, usamos a equação de uma circunferência que tem um centro na origem e, em seguida, aplicamos as translações vertical e horizontal.
Lembre-se de que a equação de uma circunferência com o centro na origem é $latex {{x}^2} + {{y}^2} = {{r}^2}$. Esta equação foi derivada usando o teorema de Pitágoras. Se reescrevermos esta equação usando o centro, teríamos $latex {{(x-0)}^2} +{{(y-0)}^2} = {{r}^2}$.
Agora, vamos considerar a seguinte circunferência:
Podemos ver que esta circunferência tem seu centro localizado no ponto (h, k). Então, se usarmos a equação da circunferência com este centro, temos:
| $latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$ |
Esta é a equação da circunferência centrada fora da origem, onde r é o raio, (x, y) é qualquer ponto localizado na circunferência e (h, k) são as coordenadas do centro da circunferência.
Exercícios resolvidos de equação da circunferência com centro fora da origem
Os exercícios a seguir facilitam a compreensão da aplicação da equação da circunferência com centro fora da origem. Tente resolver os exercícios sozinho antes de ver a resposta.
EXERCÍCIO 1
Encontre o raio e o centro da circunferência $latex {{(x-2)}^2} + {{(x-3)}^2} = 9$.
Solução
A equação geral para a circunferência é $latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$, onde $latex (h, k)$ é o centro e r é o raio. Comparando esta equação com a equação dada, temos:
$latex {{r}^2}=9$
$latex r=3$
$latex h=2$
$latex k=3$
Portanto, o raio da circunferência é 3 e o centro é (2, 3).
EXERCÍCIO 2
Qual é o raio e o centro de uma circunferência que tem a equação $latex {{(x + 4)}^2} + {{(y-5)}^2} = 16$?
Solução
Lembramos que a equação geral da circunferência é $latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$. Esta equação nos diz que $latex (h, k)$ é o centro e r é o raio do círculo. Portanto, podemos determinar o seguinte:
$latex {{r}^2}=16$
$latex r=4$
$latex h=-4$
$latex k=5$
Portanto, o raio da circunferência é 4 e o centro é (-4, 5).
EXERCÍCIO 3
Encontre a equação da circunferência que tem o centro no ponto (2, -3) e tem um raio de 4.
Solução
Substituímos os valores $latex h=2$, $latex k=-3$ e $latex r=4$ na equação geral $latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$. Então, temos:
$latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$
$latex {{(x-2)}^2}+{{(y-(-3))}^2}={{4}^2}$
$latex {{(x-2)}^2}+{{(y+3)}^2}=16$
EXERCÍCIO 4
Encontre a equação da circunferência que tem o centro no ponto (-1, 2) e no qual o ponto (2, 6) faz parte da circunferência.
Solução
Nesse caso, conhecemos os valores $latex h = -1$, $latex k = 2$. No entanto, não sabemos o raio da circunferência. Para isso, podemos usar a fórmula para a distância entre dois pontos, uma vez que essa distância representa o raio. Então, temos:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex d=\sqrt{{{(2-(-1))}^2}+{{(6-2)}^2}}$
$latex d=\sqrt{{{3}^2}+{{4}^2}}$
$latex d=\sqrt{9+16}$
$latex d=\sqrt{25}$
$latex d=5$
O raio da circunferência é $latex r = 5$. Usamos a equação geral da circunferência com esses valores:
$latex {{(x-h)}^2}+{{(y-k)}^2}={{r}^2}$
$latex {{(x-(-1))}^2}+{{(y-2)}^2}={{5}^2}$
$latex {{(x+1)}^2}+{{(y-2)}^2}=25$
Exercícios de equação da circunferência com centro fora da origem para resolver
Resolva os exercícios a seguir usando o que aprendeu sobre a equação da circunferência com o centro fora da origem. Você pode consultar os exercícios resolvidos acima, caso precise de ajuda.
Veja também
Você quer aprender mais sobre as equações da circunferência? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
