O volume de um prisma pentagonal pode ser calculado multiplicando a área da base pentagonal pela altura do prisma. Por outro lado, a área de um prisma pentagonal é calculada pela soma das áreas de todas as faces do prisma.
A seguir, vamos aprender as fórmulas que podemos usar para calcular o volume e a área dos prismas pentagonais. Além disso, vamos utilizar estas fórmulas para resolver alguns exercícios práticos.
GEOMETRIA
Relevante para…
Aprender a encontrar o volume e a área do prisma pentagonal.
GEOMETRIA
Relevante para…
Aprender a encontrar o volume e a área do prisma pentagonal.
Como calcular o volume do prisma pentagonal
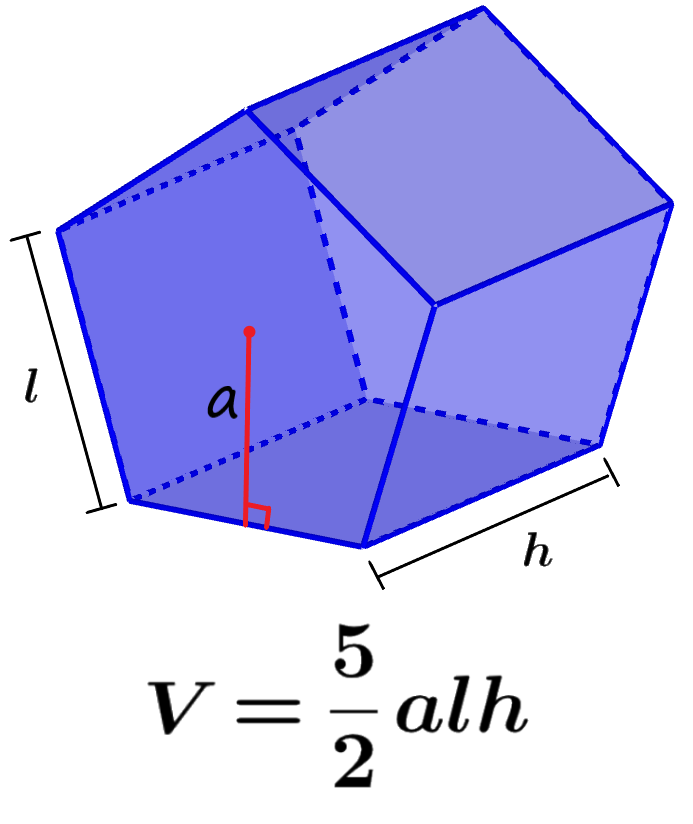
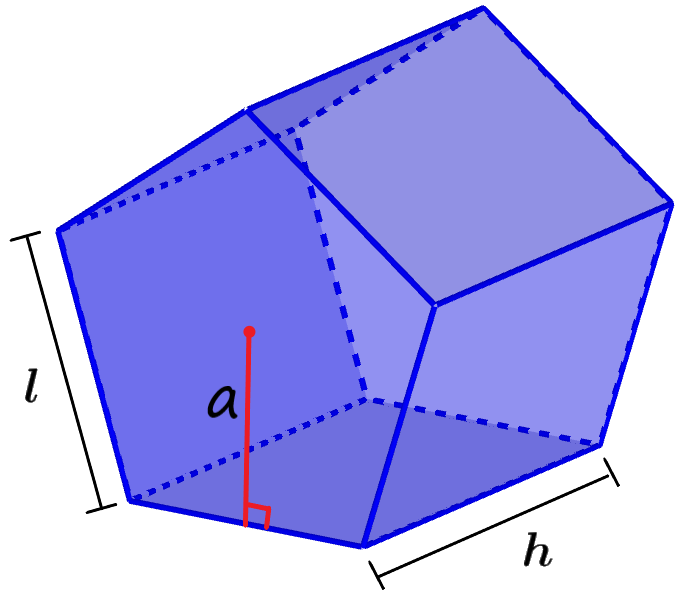
Podemos encontrar o volume de um prisma pentagonal multiplicando a área da base pela altura do prisma. Vamos lembrar que podemos usar o apótema para calcular facilmente a área dos polígonos. Portanto, temos a seguinte fórmula:
$latex V=\frac{5}{2}alh$
onde, a representa o comprimento do apótema, l representa o comprimento dos lados da base pentagonal e l representa o comprimento da altura do prisma .
Além disso, também podemos encontrar o volume de um prisma usando apenas o comprimento de sua altura e o comprimento de um dos lados de sua base pentagonal. Para isso, usamos a seguinte fórmula:
$latex V=\frac{1}{4}\sqrt{5(5+2\sqrt{5}})~{{l}^2}h$
Esta fórmula é mais complicada, mas podemos aproximá-la para a seguinte expressão:
$latex V=1,72{{l}^2}h$
Como calcular a área do prisma pentagonal
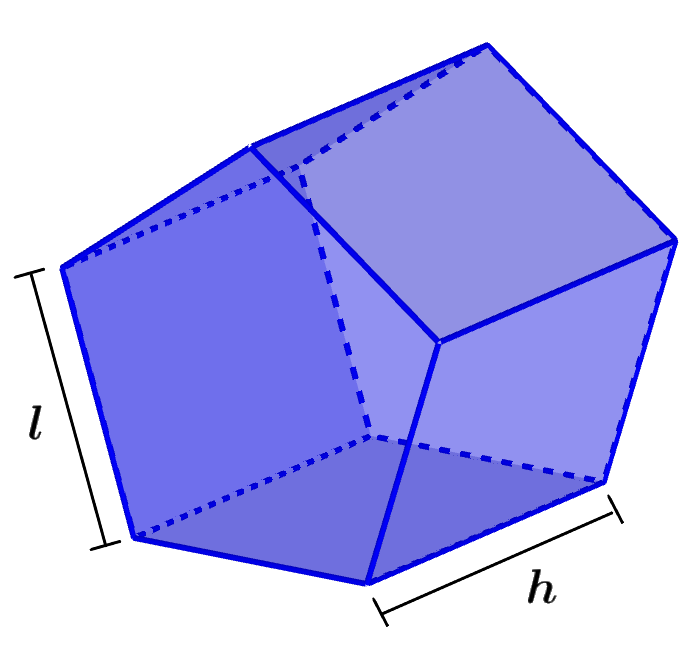
A área de superfície de qualquer figura tridimensional é encontrada adicionando as áreas de todas as suas faces. No caso de prismas pentagonais, temos duas faces pentagonais e cinco faces retangulares.
Podemos encontrar a área de cada face pentagonal usando a fórmula $latex 3,44{{l}^2}$, onde, l representa o comprimento de um dos lados da face pentagonal. Portanto, a área de ambas as faces pentagonais é $latex 6,88{{l}^2}$.
Por outro lado, a área de cada face retangular é encontrada usando a fórmula $latex lh$, onde, l é o comprimento de um dos lados da face pentagonal e h é o comprimento da altura do prisma. Portanto, a área das cinco áreas retangulares é $latex 5hl$.
Ao adicionar essas duas partes, temos a fórmula para a área da superfície de um prisma pentagonal:
$latex A_{s}=6,88{{l}^2}+5hl$
Exercícios de volume e área do prisma pentagonal resolvidos
EXERCÍCIO 1
Qual é o volume de um prisma com 6 m de altura e uma base com lados de 8 m de comprimento e apótema de 5,5 m?
Solução
Temos as seguintes informações:
- Altura do prisma, $latex h=6$
- Lados do pentágono, $latex l=8$
- Apótema, $latex a=5.5$
Usando a primeira fórmula do volume com esses dados, temos:
$latex V=\frac{5}{2}alh$
$latex V=\frac{5}{2}(5,5)(8)(6)$
$latex V=660$
O volume do prisma é de 660 m³.
EXERCÍCIO 2
Qual é a área do prisma pentagonal com 4 m de altura e 4 m de comprimento nos lados?
Solução
Temos $latex h = 4$ e $latex l = 4$. Então, usamos a fórmula para área de superfície com estes valores:
$latex A_{s}=6,88{{l}^2}+5lh$
$latex A_{s}=6,88{{(4)}^2}+5(4)(4)$
$latex A_{s}=110,1+80$
$latex A_{s}=190,1$
A área do prisma pentagonal é igual a 190,1 m².
EXERCÍCIO 3
Um prisma tem uma altura de 8 m e sua base é um pentágono com lados de 9 m e um apótema de 6,2 m. Qual é o seu volume?
Solução
Reconhecemos os seguintes dados:
- Altura do prisma, $latex h=8$
- Lados do pentágono, $latex l=9$
- Apótema, $latex a=6.2$
Substituímos esses dados na primeira fórmula do volume:
$latex V=\frac{5}{2}alh$
$latex V=\frac{5}{2}(6,2)(9)(8)$
$latex V=1116$
O volume do prisma é 1116 m³.
EXERCÍCIO 4
Se um prisma tem uma altura de 9 m e uma base pentagonal com lados de 5 m, qual é a sua área de superfície?
Solução
Usamos os comprimentos $latex h = 9$ e $latex l = 5$ na fórmula da área do prisma pentagonal:
$latex A_{s}=6,88{{l}^2}+5lh$
$latex A_{s}=6,88{{(5)}^2}+5(5)(9)$
$latex A_{s}=172+225$
$latex A_{s}=395$
A área do prisma pentagonal é igual a 395 m².
EXERCÍCIO 5
Se um prisma tem uma altura de 10 m e uma base pentagonal com lados de 5 m de comprimento, qual é o seu volume?
Solução
Temos os seguintes valores:
- Altura do prisma, $latex h=10$
- Lados do pentágono, $latex l=5$
Temos que usar a segunda fórmula do volume com estes valores:
$latex V=1,72{{l}^2}h$
$latex V=1,72{{(5)}^2}(10)$
$latex V=430$
O volume do prisma é 430 m³.
EXERCÍCIO 6
Qual é a área da superfície de um prisma pentagonal que tem lados de 6 m e uma altura de 11 m?
Solução
emos os comprimentos $latex h = 11$ e $latex l = 6$, então usamos estes valores na fórmula para a área de superfície:
$latex A_{s}=6,88{{l}^2}+5lh$
$latex A_{s}=6,88{{(6)}^2}+5(6)(11)$
$latex A_{s}=247,7+330$
$latex A_{s}=577,7$
A área do prisma é igual a 577,7 m².
EXERCÍCIO 7
Um prisma tem uma base pentagonal com lados de 3 m de comprimento. Se sua altura é de 5 m, qual é o seu volume?
Solução
Temos o seguinte:
- Altura do prisma, $latex h=5$
- Lados do pentágono, $latex l=3$
Usando a segunda fórmula com esses valores, temos:
$latex V=1,72{{l}^2}h$
$latex V=1,72{{(3)}^2}(5)$
$latex V=77,4$
O volume do prisma é de 77,4 m³.
EXERCÍCIO 8
Se um prisma pentagonal tem lados com 8 m de comprimento e 12 m de altura, qual é sua área de superfície?
Solução
Substituímos os comprimentos $latex h = 12$ e $latex l = 8$ na fórmula para a área de superfície:
$latex A_{s}=6,88{{l}^2}+5lh$
$latex A_{s}=6,88{{(8)}^2}+5(8)(12)$
$latex A_{s}=440,3+480$
$latex A_{s}=920,3$
A área do prisma é igual a 920,3 m².
EXERCÍCIO 9
Qual é o volume de um prisma com 12 m de altura e uma base pentagonal com lados de 6 m?
Solução
Temos os seguintes valores:
- Altura do prisma, $latex h=12$
- Lados do pentágono, $latex l=6$
Se usarmos a segunda fórmula, temos:
$latex V=1,72{{l}^2}h$
$latex V=1,72{{(6)}^2}(12)$
$latex V=743,04$
O volume do prisma é 743,04 m³.
Exercícios de volume e área do prisma pentagonal para resolver
Se tivermos um prisma pentagonal com 7 m de altura e 3 m de lado, qual é a área de sua superfície?
Escreva a resposta com uma casa decimal.
Veja também
Você quer aprender mais sobre prismas pentagonais? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
