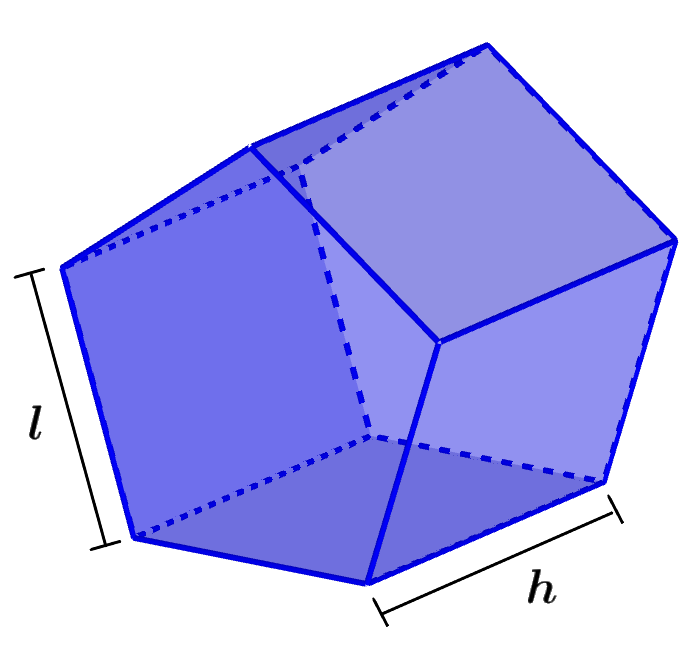
O prisma pentagonal é uma figura tridimensional formada por duas bases pentagonais. As bases pentagonais são congruentes e paralelas entre si. Essas bases são conectadas por cinco faces laterais retangulares. Esses prismas são caracterizados por terem um total de 7 faces, 10 vértices e 15 arestas. Os prismas pentagonais também são considerados heptaedros.
A seguir, conheceremos algumas das características mais importantes deste tipo de prismas. Além disso, conheceremos suas fórmulas mais utilizadas e as aplicaremos para resolver alguns exercícios.
Definição de um prisma pentagonal
Um prisma pentagonal é um prisma que possui duas bases pentagonais e cinco faces retangulares laterais. Esses prismas são um tipo de heptaedro com 7 faces, 10 vértices e 15 arestas.
Cada vértice do prisma pentagonal é um ponto onde três faces, duas faces retangulares e uma face pentagonal se encontram. A seguir está um diagrama de um prisma pentagonal.
Existem dois tipos principais de prismas pentagonais:
- Prismas pentagonais regulares
- Prismas pentagonais retos
Prismas pentagonais regulares
Os prismas pentagonais regulares são formados quando todos os lados da base pentagonal têm o mesmo comprimento. Nestes prismas, todas as faces laterais retangulares são congruentes, ou seja, possuem as mesmas dimensões. As faces laterais são freqüentemente chamadas de lados do prisma.
Prismas Pentagonais Retos
Um prisma pentagonal é reto quando tem duas bases pentagonais congruentes e paralelas entre si e quando as faces laterais formam um ângulo reto (90 graus) com as bases.
Características fundamentais do prisma pentagonal
A seguir estão as características mais importantes de um prisma pentagonal:
- As bases do prisma são pentágonos.
- As bases são congruentes e paralelas entre si
- As faces laterais do prisma são retângulos.
- Se o prisma for regular, as faces laterais são congruentes.
- Esses prismas têm 7 faces, 10 vértices e 15 arestas.
- Duas faces retangulares e uma face pentagonal se encontram em cada vértice.
- Um prisma pentagonal é reto quando as bases formam ângulos de 90 graus com as faces laterais.
Fórmulas importantes do prisma pentagonal
Os prismas pentagonais são figuras 3D, então suas fórmulas mais importantes são a fórmula do volume e a fórmula da área de superfície.
Fórmula do volume do prisma pentagonal
O volume de um prisma é igual à área da base vezes a altura do prisma. Nesse caso, temos a fórmula:
| $latex V=\frac{5}{2}alh$ |
onde, a representa o comprimento do apótema do hexágono, l é o comprimento de um dos lados do hexágono e h é a altura do prisma.
Fórmula da área do prisma pentagonal
A área da superfície de um prisma é igual à soma das áreas de todas as suas faces. Temos duas faces pentagonais e cinco faces retangulares, então sua fórmula para a área de superfície é:
| $latex A_{s}=5al+5lh$ |
Exemplos de problemas do prisma pentagonal
Os exercícios a seguir são resolvidos aplicando-se as fórmulas do prisma pentagonal vistas acima.
EXEMPLO 1
Se um prisma pentagonal tem um apótema de 5,5 m, uma altura de 6 m e lados de 8 m de comprimento, qual é o seu volume?
Solução: Temos os comprimentos $latex a = 5,5$, $latex l = 6$ e $latex h = 8$. Usando esses valores na fórmula de volume, temos:
$latex V=\frac{5}{2}alh$
$latex V=\frac{5}{2}(5,5)(8)(6)$
$latex V=251,3$
O volume do prisma é de 660 m³.
EXEMPLO 2
Qual é o volume de um prisma que tem uma altura de 10 m e uma base pentagonal com lados de 9 m e um apótema de 6,2 m?
Solução: Temos os valores $latex a=6,2$, $latex l=9$ e $latex h=10$. Usamos a fórmula do volume com esses valores:
$latex V=\frac{5}{2}alh$
$latex V=\frac{5}{2}(6,2)(9)(10)$
$latex V=1395$
O volume do prisma é de 1395 m³.
EXEMPLO 3
Qual é a área do prisma pentagonal que tem uma altura de 10 m, um apótema de 5,5 m e lados de 6 m de comprimento?
Solução: Temos os comprimentos $latex h=10$, $latex a=5,5$ e $latex l=6$, então usamos esses valores na fórmula para área de superfície:
$latex A_{s}=5al+5lh$
$latex A_{s}=5(5,5)(6)+5(6)(10)$
$latex A_{s}=165+300$
$latex A_{s}=465$
A área do prisma é 465 m².
EXEMPLO 4
Qual é a área da superfície de um prisma que tem uma altura de 6 m, um apótema de 4,8 m e lados de 8 m de comprimento?
Solução: Podemos usar os valores dados na fórmula para a área de superfície:
$latex A_{s}=5al+5lh$
$latex A_{s}=5(4.8)(8)+5(8)(6)$
$latex A_{s}=192+240$
$latex A_{s}=854,5$
A área do prisma é 432 m².
Veja também
Você quer aprender mais sobre prismas pentagonais? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
