O teorema do ângulo inscrito afirma que quando temos um ângulo central e um ângulo inscrito se interceptam no mesmo arco do círculo, o ângulo central é o dobro do ângulo inscrito. Dependendo de como os ângulos estão localizados, podemos ter três casos diferentes desse teorema. Cada um desses casos precisa de um método diferente para ser comprovado.
A seguir, aprenderemos sobre as diferentes provas que podemos usar para provar o teorema do ângulo inscrito.
Explicação do Teorema do Ângulo Inscrito
O teorema do ângulo inscrito afirma que quando o ângulo central e o ângulo inscrito compartilham extremidades no círculo, o valor do ângulo central é duas vezes o valor do ângulo inscrito.
Lembre-se de que um ângulo inscrito é um ângulo dentro do círculo formado no encontro de duas cordas.
Um ângulo central é um ângulo no interior de um círculo, em que o vértice é o centro do círculo e os lados são os raios.
No diagrama abaixo, o ângulo verde é um ângulo central e o ângulo rosa é um ângulo inscrito.
Prova do caso 1: Ângulo inscrito entre uma corda e o diâmetro do círculo
Este caso pode ser observado no diagrama a seguir:
Vamos provar que α=2β.
Neste diagrama, o triângulo ABC é um triângulo isósceles, pois os segmentos AC e BC são raios do círculo e temos AC=BC. Então os ângulos ∠CAB e ∠ABC são iguais. Ou seja, temos ∠CAB=∠ABC=β.
O diâmetro AD é uma linha reta, então o ângulo ∠BCA=(180-α)°.
Sabemos que os ângulos de um triângulo somam 180°, então temos:
∠CAB+∠ABC+∠BCA=180°
Agora, simplificamos os ângulos com seus valores conhecidos e temos:
β+β+180°-α=180°
Simplificando e resolvendo, temos:
β+β+180°-α=180°
2β-α=0
2β=α
Provamos o teorema.
Prova do caso 2: Diâmetro entre os lados do ângulo inscrito
No diagrama a seguir, podemos observar o segundo caso:
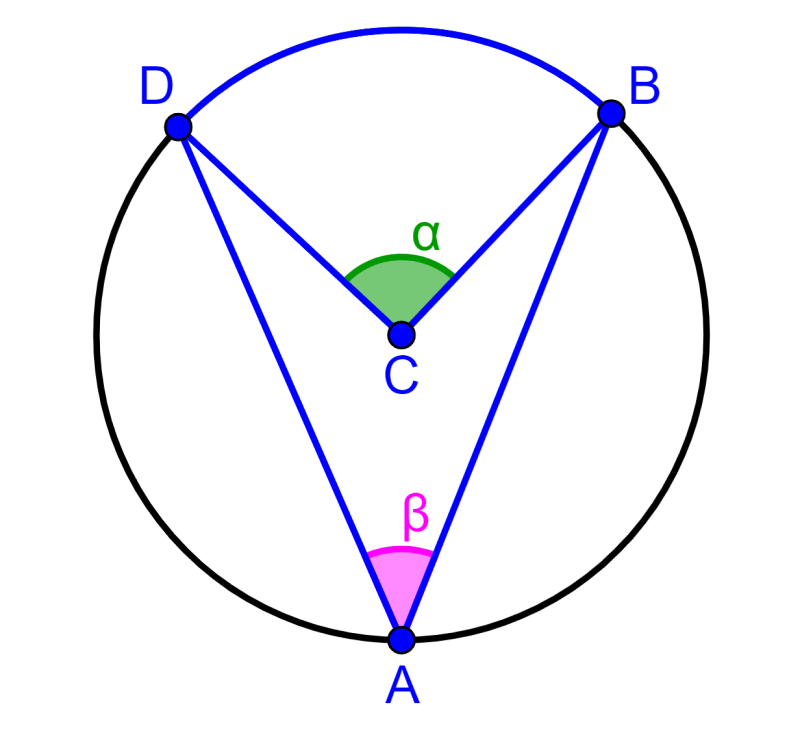
Vamos provar que 2β=α.
Podemos traçar o diâmetro do círculo e representar os ângulos importantes.
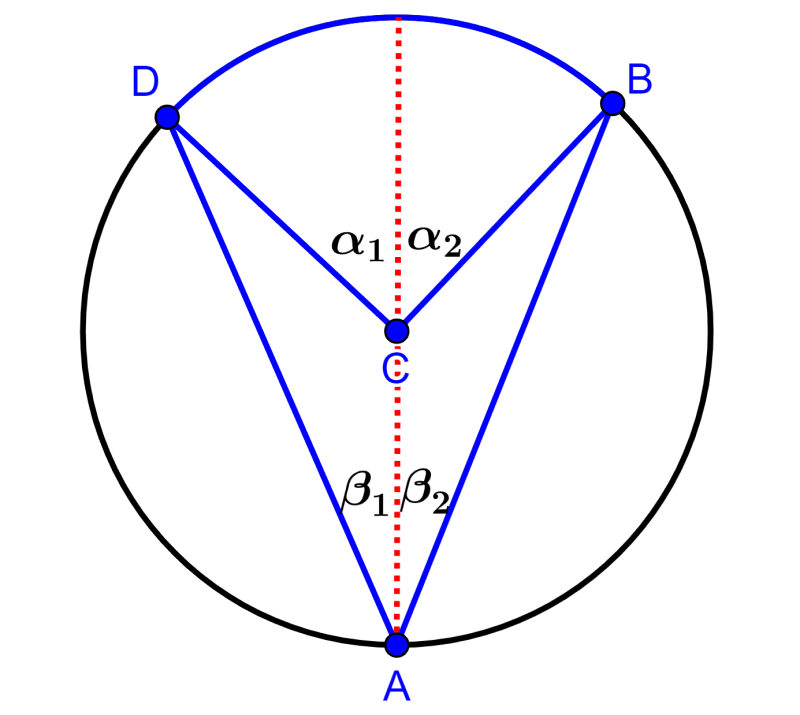
Podemos ver que o diâmetro divide os ângulos α e β. Então temos:
$latex \alpha_{1}+\alpha_{2}=\alpha$
$latex \beta_{1}+\beta_{2}=\beta$
Levando em conta o primeiro caso que vimos acima, podemos deduzir o seguinte:
$latex 2\beta_{1}=\alpha_{1}$
$latex 2\beta_{2}=\alpha_{2}$
Agora, podemos somar os ângulos e simplificar usando $latex \alpha=\alpha_{1}+\alpha_{2}$ e $latex \beta=\beta_{1}+\beta_{2}$:
$latex 2\beta_{1}+2\beta_{2}=\alpha_{1}+\alpha_{2}$
$latex 2\beta=\alpha$
Provamos o teorema.
Prova do caso 3: Diâmetro fora dos lados do ângulo inscrito
Este caso é representado no diagrama a seguir:
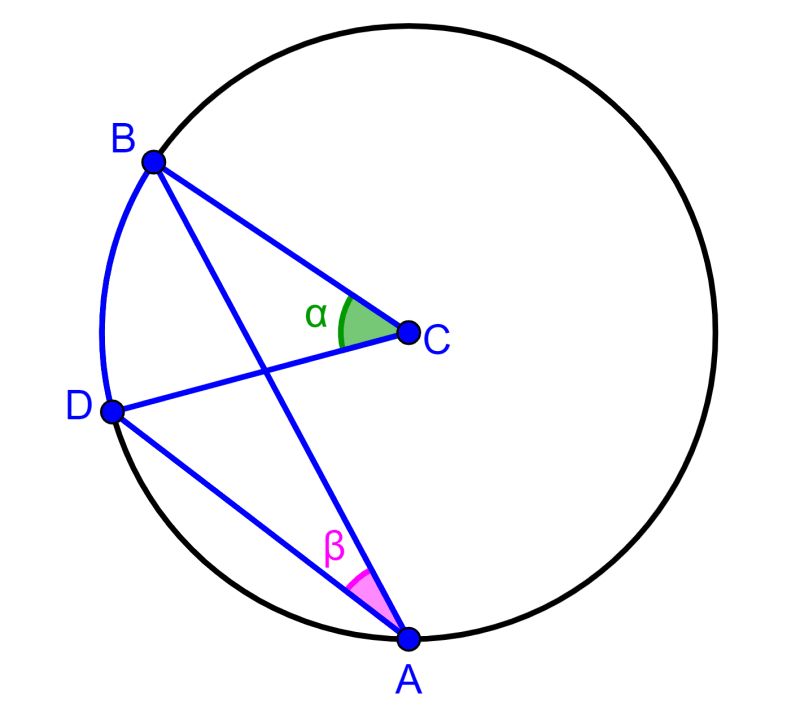
Vamos provar que 2β=α.
Semelhante ao caso anterior, vamos traçar o diâmetro do círculo e representar os ângulos importantes.
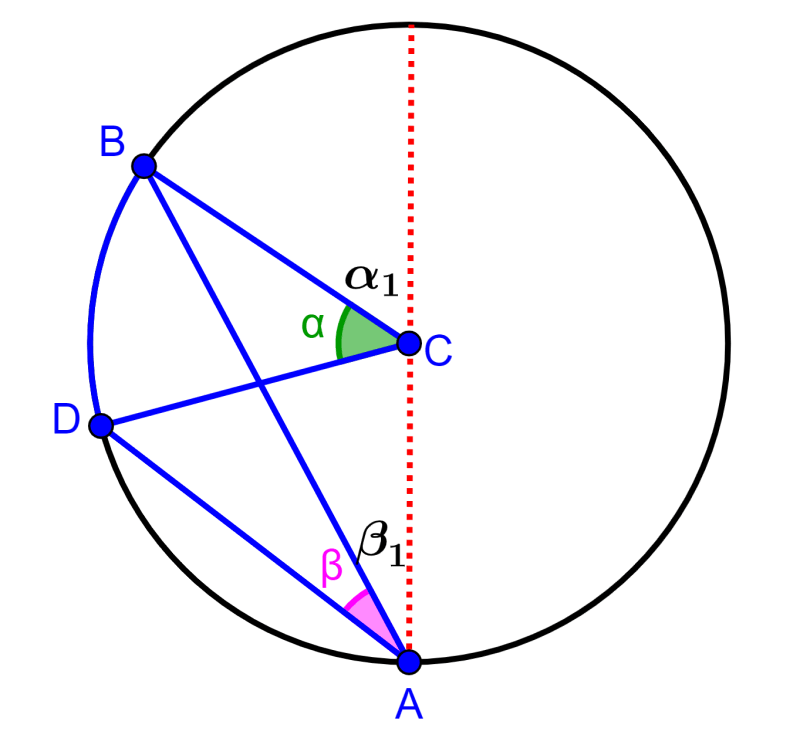
Novamente, sabemos que $latex 2\beta_{1}=\alpha_{1}$. Então temos:
$latex 2(\beta_{1}+\beta)=\alpha+\alpha_{1}$
Substituindo $latex 2\beta_{1}=\alpha_{1}$, temos:
$latex 2(\beta_{1}+\beta)=\alpha+2\beta_{1}$
$latex 2\beta_{1}+2\beta=\alpha+2\beta_{1}$
$latex 2\beta=\alpha$
Provamos o teorema.
Veja também
Interessado em aprender mais sobre ângulos inscritos e outros tipos de ângulos? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
