Distância entre ponto e reta – Fórmulas e exercícios

Qual é a distância entre um ponto e uma reta?

A distância entre um ponto e uma reta é a distância mais curta que pode uni-los. Ou seja, é o menor comprimento possível que precisamos para mover do ponto para um ponto na reta. Esta distância será sempre perpendicular à reta dada.

Por exemplo, vamos considerar a seguinte reta L e um ponto p que não faz parte da reta:

Para medir a distância da reta ao ponto p, podemos usar a equação de uma reta e a fórmula da distância. Além disso, também consideramos um triângulo retângulo XYZ, que tem um ângulo reto em Y:

Neste triângulo, o ângulo Y mede 90° e o segmento XZ é a hipotenusa. A hipotenusa XZ será sempre maior que o segmento perpendicular de X a YZ. Então, podemos usar isso no diagrama a seguir:

O segmento XY é perpendicular à reta L. Por outro lado, Z pode ser qualquer ponto da reta R. Podemos ver que XY sempre será menor que XZ, não importa onde Z esteja localizado na reta.

Isso significa que a distância mais curta entre um ponto e uma reta será sempre um segmento perpendicular do ponto à reta.

Prova da fórmula para a distância entre ponto e reta

A distância perpendicular entre um ponto $latex P(x_{1},~y_{1})$ e uma reta $latex ax+by+c=0$ pode ser encontrada usando a seguinte fórmula:

$$d=\left| \frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right|$$

Podemos derivar esta fórmula usando o seguinte diagrama:

O ponto $latex Q(x_{1},~y_{2})$ está na reta $latex ax+by+c=0$ e está diretamente abaixo de P.

Usando o ponto Q na equação da reta, temos $latex ax_{1}+by_{2}+c=0$. Se resolvermos $latex y_{2}$, teremos:

$$y_{2}=-\left(\frac{ax_{1}+c}{b}\right)$$

Como os pontos P e Q estão na mesma coordenada x, temos: $latex PQ=y_{1}-y_{2}$. Usando isso na equação obtida acima, temos:

$$PQ=y_{1}+\frac{ax_{1}+c}{b}$$

$$=\frac{ax_{1}+by_{1}+c}{b}$$

Agora, olhando para o diagrama, podemos deduzir que d é igual ao cosseno de θ multiplicado por PQ: $latex d=PQ\cos(\theta)$. Então temos:

$$d=\frac{ax_{1}+by_{1}+c}{b}\cos(\theta)~~[1]$$

Resta-nos apenas encontrar uma expressão para cos(θ) para completar a derivação da fórmula.

Usando o diagrama novamente em conjunto com os teoremas dos ângulos, podemos deduzir que o ângulo θ é igual ao ângulo α. Além disso, como podemos escrever a equação da reta l como $latex y=-\frac{a}{b}x-c$, o declive de l é $latex-\frac{a}{b}$.

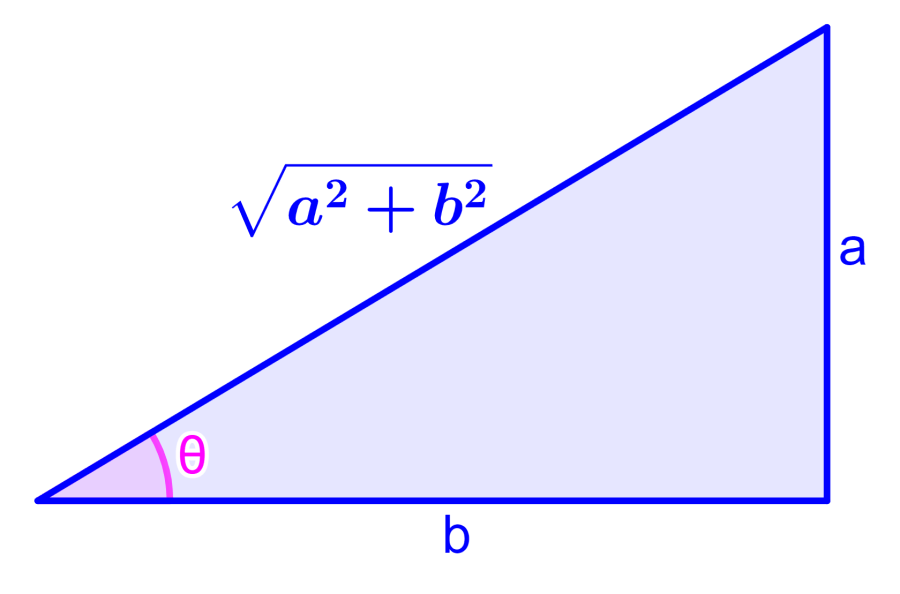
Isso significa que $latex \tan(\theta)=\tan(\alpha)=\frac{a}{b}$. Lembrando que a tangente é igual ao lado oposto sobre o lado adjacente, podemos obter o seguinte diagrama, onde usamos o teorema de Pitágoras para obter a hipotenusa:

Então temos:

$$\cos(\theta)=\frac{b}{\sqrt{a^2+b^2}}~~[2]$$

Substituindo a equação [2] na equação [1], temos:

$$d=\left(\frac{ax_{1}+by_{1}+c}{b}\right)\frac{b}{\sqrt{a^2+b^2}}$$

$$d=\left(\frac{ax_{1}+by_{1}+c}{\sqrt{a^2+b^2}}\right)$$

Nota: O sinal do valor absoluto é dado ao resultado, pois nesta prova assumimos que a reta tem declive negativo e que o ponto P está acima da reta. Se o ponto P estivesse abaixo da reta, teríamos introduzido um sinal negativo na fórmula.

Distância entre ponto e reta – Exercícios resolvidos

Os exercícios a seguir são resolvidos usando a fórmula para a distância entre um ponto e uma reta. Cada exercício tem sua respectiva solução, mas tente resolver os exercícios você mesmo.

Distância entre ponto e reta – Exercícios para resolver

Tente resolver os exercícios a seguir aplicando a fórmula da distância entre ponto e uma reta. Clique em “Verificar” para verificar se a resposta selecionada está correta.

Veja também

Interessado em aprender mais sobre equações de retas? Dê uma olhada nessas páginas:

• Equação de uma Reta na Forma de Interceptação-Declive
• Ângulo entre duas retas – Fórmulas e exercícios
• Declive de uma Reta – Fórmula e Exercícios