O ortocentro de um triângulo pode ser encontrado usando dois métodos principais. Podemos representar graficamente as alturas do triângulo e encontrar o ponto de interseção. Alternativamente, podemos encontrar as coordenadas do ortocentro algebricamente.
Neste artigo, aprenderemos como encontrar o ortocentro de um triângulo usando os dois métodos listados. Em seguida, vamos resolver alguns exercícios práticos.
O que é o ortocentro de um triângulo?
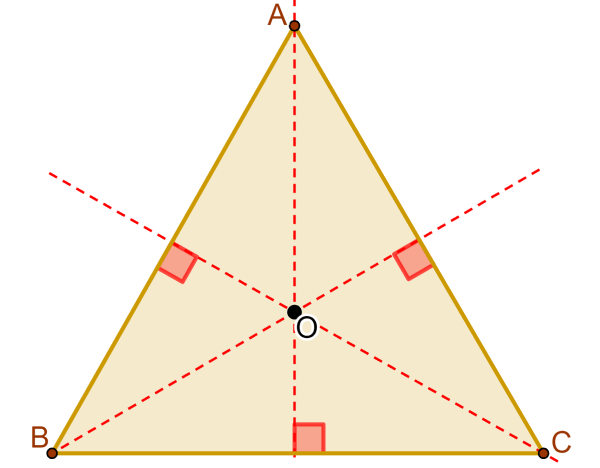
O ortocentro de um triângulo é o ponto de intersecção das três alturas do triângulo. No diagrama abaixo, podemos ver que o ponto O é o ortocentro:
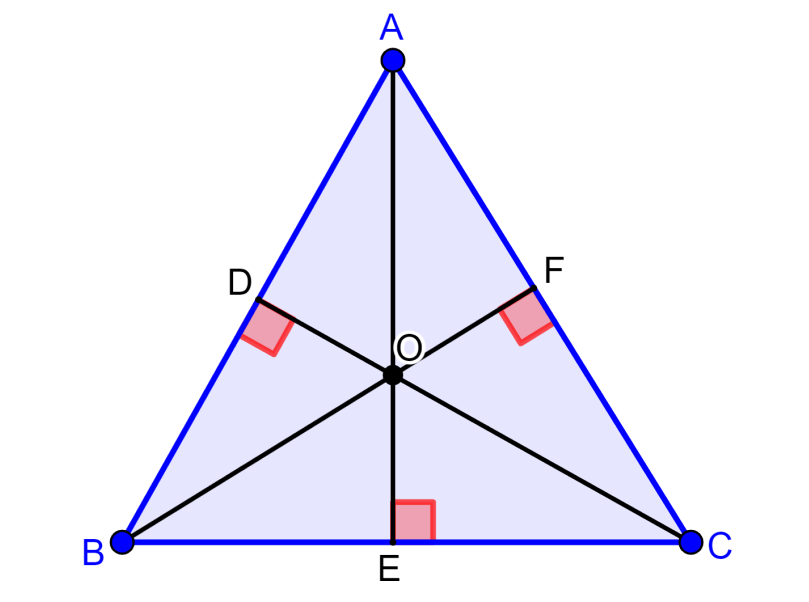
Lembre-se que as alturas do triângulo são os segmentos perpendiculares que conectam um vértice com seu lado oposto. As alturas sempre formam um ângulo de 90° com o lado correspondente.
Ortocentro de triângulos comuns
Dependendo do tipo de triângulo que temos, a localização do ortocentro varia.
Ortocentro de triângulos agudos
O ortocentro de todos os triângulos agudos sempre está dentro do triângulo. Lembre-se que um triângulo agudo é caracterizado por todos os seus ângulos internos serem menores que 90°.
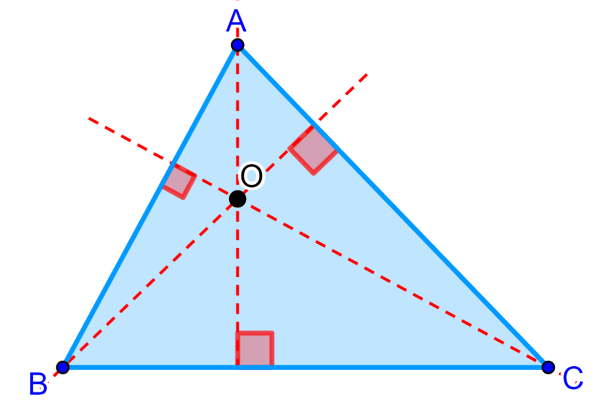
Ortocentro de triângulos obtusos
O ortocentro de todos os triângulos obtusos sempre fica fora do triângulo. Lembre-se que um triângulo obtuso é caracterizado por ter um ângulo maior que 90°.
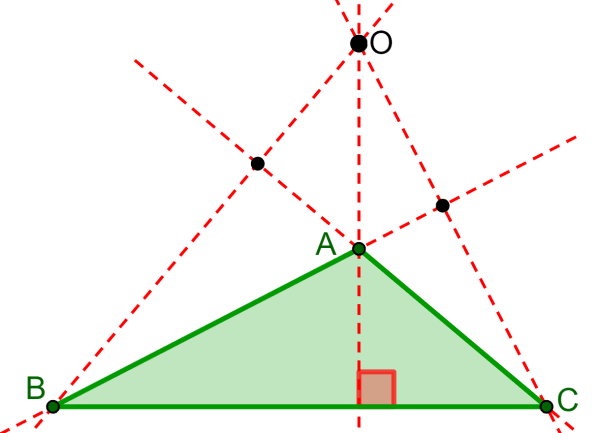
Ortocentro de triângulos retângulos
O ortocentro de todos os triângulos retângulos está localizado no vértice central do triângulo retângulo. Lembre-se que um triângulo retângulo tem um ângulo de 90°.
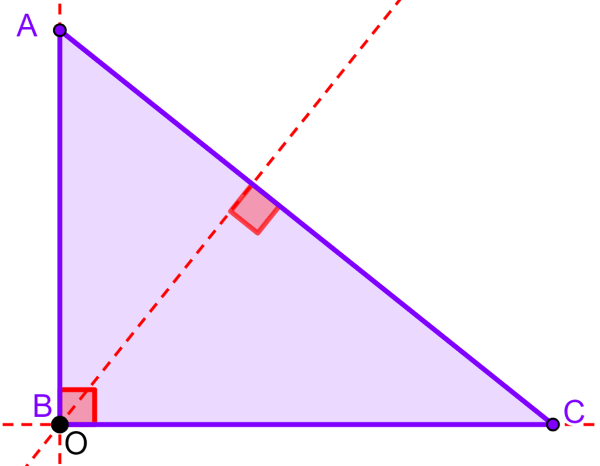
Ortocentro de triângulos equiláteros
O ortocentro de todos os triângulos equiláteros está localizado na mesma posição que o baricentro do triângulo. Lembre-se de que os triângulos equiláteros têm os três lados do mesmo comprimento.
Encontrar o ortocentro de um triângulo graficamente
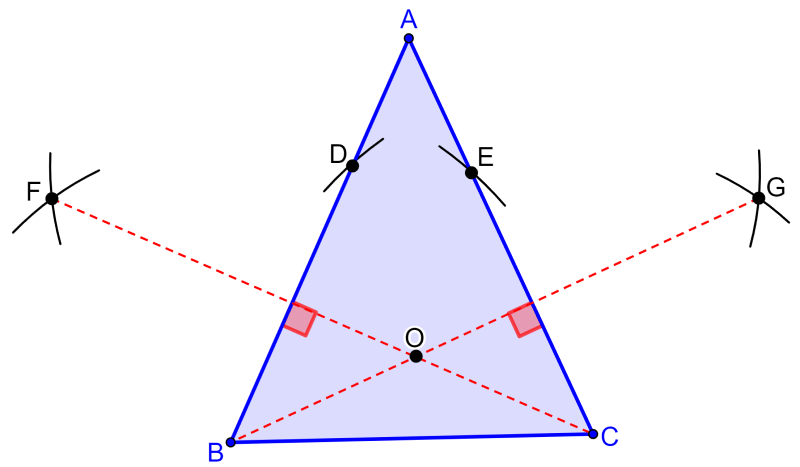
Podemos encontrar o ortocentro de um triângulo graficamente traçando duas alturas do triângulo e encontrando seu ponto de interseção.
Por sua vez, podemos encontrar as alturas desenhando retas perpendiculares dos vértices aos lados opostos. Fazemos isso com os seguintes passos:
Passo 1: Usando um raio igual a BC e centrando no ponto B, desenhamos um arco no lado AC para formar o ponto E.
Passo 2: Usando um raio igual a BC e centrando no ponto C, desenhamos um arco no lado AB para formar o ponto D.
Passo 3: Usando um raio igual a BD, desenhamos arcos de interseção de B e D para formar o ponto F e desenhamos o segmento CF.
Passo 4: Usando um raio igual a CE, desenhamos arcos de interseção de C e E para formar o ponto G e desenhar o segmento BG.
Passo 5: Marcamos o ponto de intersecção dos segmentos CF e BG.
Os segmentos CF e BG são perpendiculares aos lados AB e AC respectivamente. Isso significa que eles representam as alturas do triângulo. Portanto, o ponto de interseção é o ortocentro do triângulo.
Encontrar o ortocentro de um triângulo algebricamente
O ortocentro de um triângulo pode ser encontrado algebricamente usando as coordenadas dos vértices do triângulo. Podemos seguir o processo usando o triângulo a seguir.
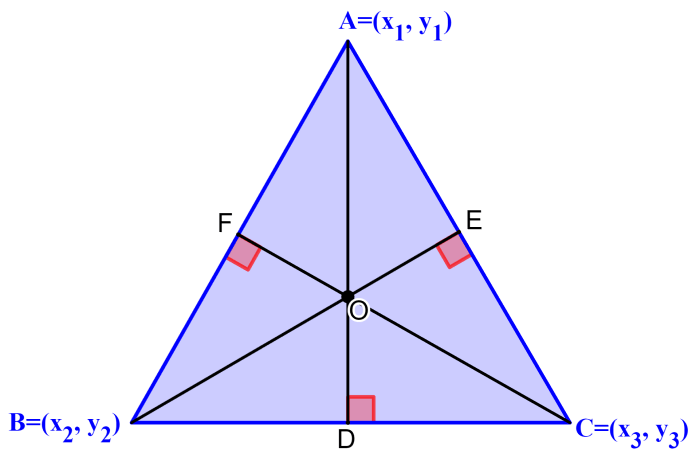
Neste triângulo, A($latex x_{1},~y_{1}$), B($latex x_{2},~y_{2}$), C($latex x_{3},~y_{ 3}$) são os vértices e AD, BE e CF são as alturas. O ponto O é o ortocentro, pois é o ponto de interseção.
Passo 1: Para encontrar as alturas, temos que começar encontrando os declives dos lados do triângulo. Para isso, usamos a fórmula do declive:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
Representando o declive da reta AC como $latex m_{AC}$, temos:
$latex m_{AC}=\frac{y_{3}-y_{1}}{x_{3}-x_{1}}$
Da mesma forma, temos também:
$latex m_{BC}=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}$
Passo 2: Uma vez que temos os declives dos lados, podemos encontrar os declives das alturas assumindo que as alturas são perpendiculares aos lados. O declive de uma reta perpendicular a outra reta é:
Declive da reta perpendicular $latex =-\frac{1}{m}$
onde m é o declive da reta original.
Assim, os declives das alturas são:
Declive de BE: $latex m_{BE}=-\frac{1}{m_{AC}}$
Declive de AD: $latex m_{AD}=-\frac{1}{m_{BC}}$
Passo 3: Podemos encontrar as equações das retas que passam por BE e AD usando a forma ponto-declive. Então temos:
$latex m_{BE}=\frac{y-y_{2}}{x-x_{2}}$
$latex m_{AD}=\frac{y-y_{1}}{x-x_{1}}$
Passo 4: Como sabemos os valores de $latex (x_{1},~y_{1})$ e $latex (x_{2},~y_{2})$, podemos usar qualquer método para resolver o sistema de equações e encontre os valores de x e y, que são as coordenadas do ortocentro.
Exemplos resolvidos do ortocentro de um triângulo
Nos exemplos a seguir, podemos ver como encontrar as coordenadas do ortocentro de um triângulo algebricamente.
EXEMPLO 1
Se um triângulo tem vértices A(5, 7), B(2, 3) e C(6, 4), encontre os declives de seus lados.
Solução: Temos as seguintes coordenadas:
- $latex (x_{1},~y_{1})=(5, ~7)$
- $latex (x_{2},~y_{2})=(2,~3)$
- $latex (x_{3},~y_{3})=(6,~4)$
Usando a fórmula do declive, podemos determinar o declive de cada lado.
Declive de CA:
$latex m_{AC}=\frac{y_{3}-y_{1}}{x_{3}-x_{1}}$
$latex m_{AC}=\frac{4-7}{6-5}$
$latex m_{AC}=-3$
Declive de BA:
$latex m_{BA}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}$
$latex m_{BA}=\frac{7-3}{5-2}$
$latex m_{BA}=\frac{4}{3}$
Declive de BC:
$latex m_{BC}=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}$
$latex m_{BC}=\frac{4-3}{6-2}$
$latex m_{BC}=\frac{1}{4}$
EXEMPLO 2
Use os declives encontrados no Exemplo 1 para determinar as coordenadas do ortocentro do triângulo.
Solução: Temos que encontrar os declives das retas perpendiculares aos lados, pois elas correspondem às alturas do triângulo. Então temos:
- $latex m_{AE}=$ perpendicular a BC
- $latex m_{BF}=$ perpendicular a AC
- $latex m_{CD}=$ perpendicular a AB
O declive de uma reta perpendicular é igual a $latex -\frac{1}{m}$, onde, m é o declive da reta original, temos:
$latex m_{AE}=-4$
$latex m_{BF}=\frac{1}{3}$
$latex m_{CD}=-\frac{3}{4}$
Usando a forma ponto-declive, $latex y-y_{1}=m(x-x_{1})$, podemos encontrar as equações das retas perpendiculares. Precisamos apenas de duas equações para encontrar o ponto de interseção.
Usamos o declive de CD e o ponto C=(6, 4) para encontrar a primeira equação:
$latex y-4=-\frac{3}{4}(x-6)$
$latex 4(y-4)=-3(x-6)$
$latex 4y-16=-3x+18$
$latex 3x+4y=34$
Agora, usamos o declive de BF e o ponto B=(2, 3) para encontrar a segunda equação:
$latex y-3=\frac{1}{3}(x-2)$
$latex 3(y-3)=x-2$
$latex 3y-9=x-2$
$latex -x+3y=7$
Qualquer método pode ser usado para resolver o sistema de duas equações e encontramos a solução $latex x=\frac{74}{18},~ y=\frac{55}{13}$.
Esta solução representa o ponto de intersecção das linhas. Portanto, as coordenadas do ortocentro são $latex (\frac{74}{18},~\frac{55}{13})$.
Exercícios para resolver o ortocentro de um triângulo
Resolva os exercícios a seguir usando o método algébrico para encontrar as coordenadas do ortocentro.
Veja também
Interessado em aprender mais sobre o baricentro, incentro, ortocentro e circuncentro de um triângulo? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
