O circuncentro de um triângulo pode ser encontrado usando cinco métodos diferentes. Três métodos consistem em usar diferentes técnicas algébricas e geométricas para determinar as equações das mediatrizes e determinar o ponto de interseção. O quarto método é usar uma fórmula com as coordenadas dos vértices e as medidas dos ângulos. O quinto método é determinar o circuncentro graficamente.
Neste artigo, aprenderemos como encontrar o circuncentro de um triângulo usando cinco métodos diferentes. Vamos resolver alguns exercícios práticos.
O que é o circuncentro de um triângulo?
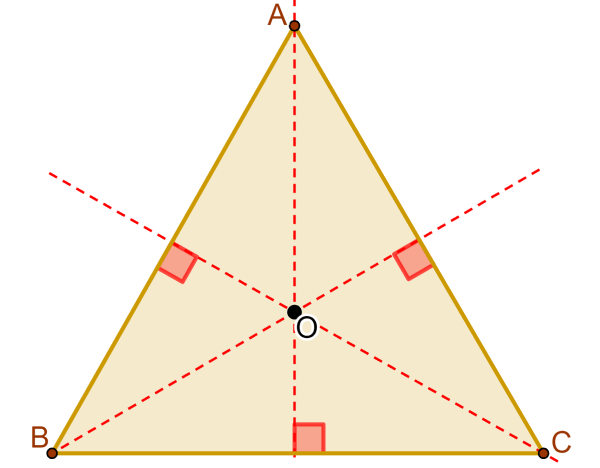
O circuncentro é o ponto de intersecção das mediatrizes dos lados do triângulo. No diagrama abaixo, podemos ver que o ponto O é o circuncentro:
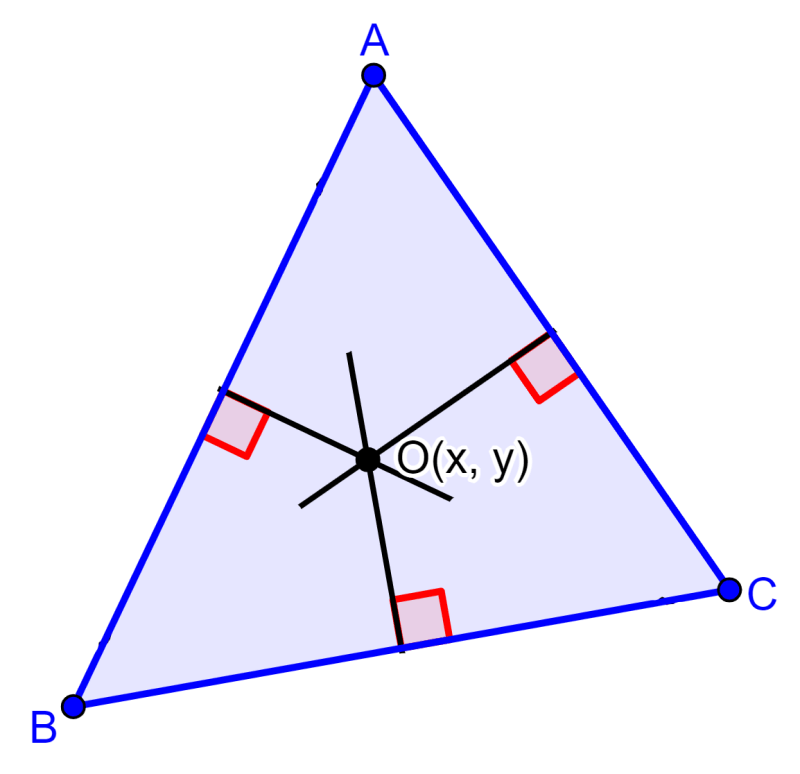
Lembre-se que as mediatrizes são os segmentos perpendiculares que passam pelos pontos médios de cada lado do triângulo.
Alternativamente, podemos definir o circuncentro como o centro do círculo circunscrito, que passa por todos os três vértices do triângulo.
Circuncentro de triângulos comuns
A localização do circuncentro varia dependendo do tipo de triângulo que temos.
Circuncentro de triângulos agudos
O circuncentro de todos os triângulos agudos sempre está dentro do triângulo.
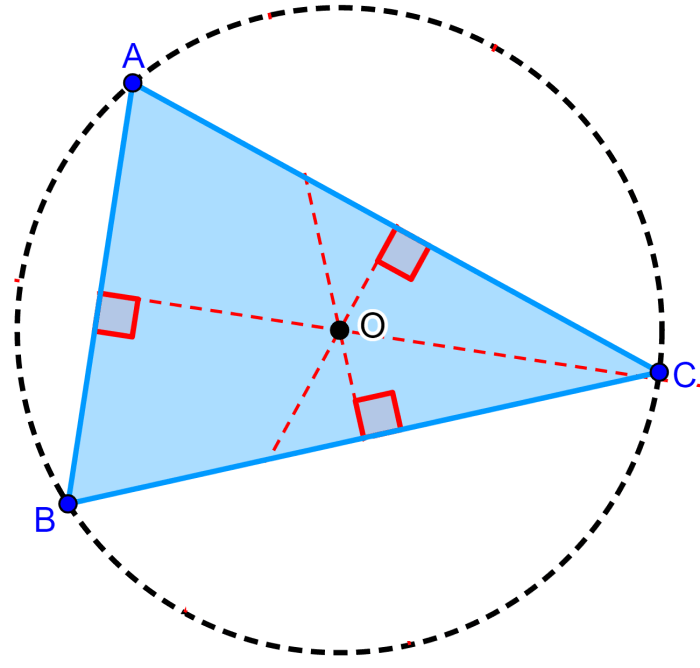
Circuncentro de triângulos obtusos
O circuncentro de todos os triângulos obtusos sempre fica fora do triângulo.
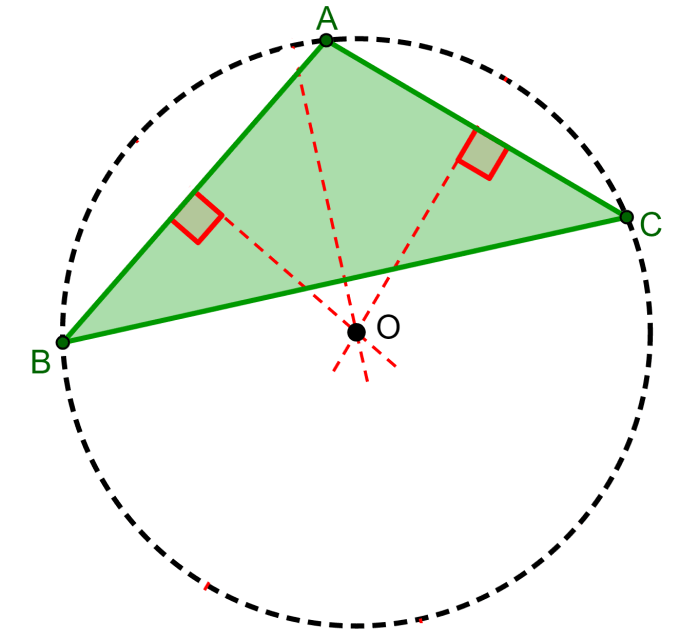
Circuncentro dos triângulos retângulos
O circuncentro de todos os triângulos retângulos está localizado na hipotenusa do triângulo retângulo. Além disso, a hipotenusa do triângulo retângulo corresponde ao diâmetro do círculo circunscrito.
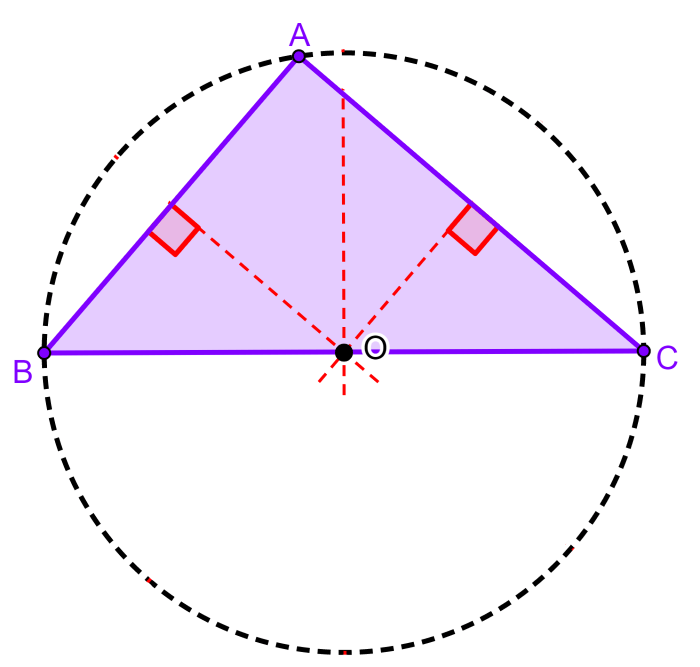
Circuncentro de triângulos equiláteros
O circuncentro, ortocentro, incentro e baricentro de todos os triângulos equiláteros estão localizados na mesma posição.
Encontrar o circuncentro de um triângulo graficamente
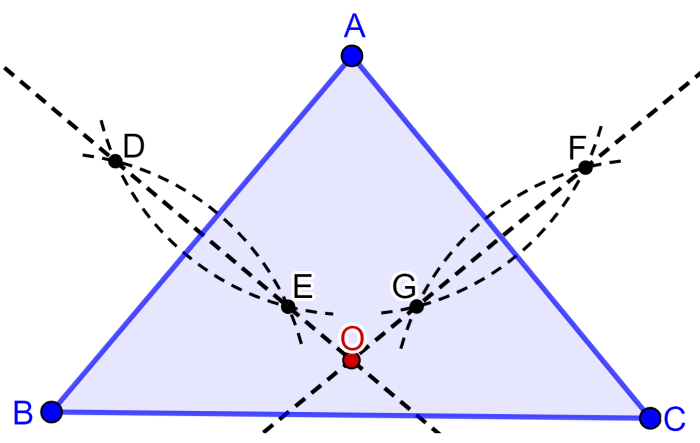
Para encontrar graficamente o circuncentro de um triângulo, temos que desenhar as mediatrizes e encontrar o ponto de interseção.
Podemos usar um compasso para determinar duas mediatrizes perpendiculares seguindo estes passos:
Passo 1: Desenhamos um arco no lado AB usando o vértice B como centro e um raio com comprimento ligeiramente maior que a metade de AB. Por exemplo, se AB for 4 unidades, podemos usar um raio de 2,5.
Passo 2: Usamos o vértice C como centro com o mesmo raio do passo 1 e desenhamos um arco no lado AB.
Passo 3: Desenhamos uma linha que passa pelos pontos D e E. Esta é uma mediatriz.
Passo 4: Seguimos um processo semelhante para desenhar arcos de interseção de C e A para formar os pontos F e G e desenhar uma linha através desses pontos.
Passo 5: Marcamos o ponto de interseção das linhas desenhadas.
As linhas traçadas são as mediatrizes, pois são perpendiculares aos seus lados correspondentes e passam pelo ponto médio dos lados. Portanto, o ponto de interseção é o circuncentro do triângulo.
Encontrar o circuncentro de um triângulo algebricamente
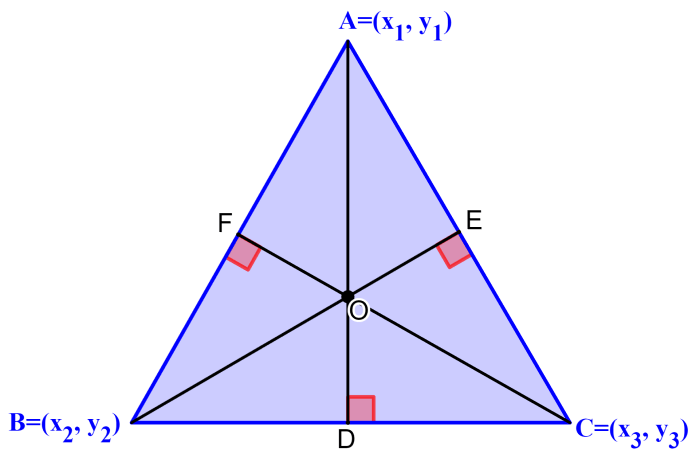
Podemos encontrar o circuncentro de um triângulo usando quatro métodos principais. Vamos usar o seguinte triângulo que tem os vértices $latex A=(x_{1},~y_{1})$, $latex B=(x_{2},~y_{2})$ e $latex C= (x_{3},~y_{3})$. O circuncentro está localizado em (x, y).
Método 1: Usando a Fórmula da Distância
Passo 1: Usando a fórmula da distância, $latex d=\sqrt{(x-x_{1})^2+(y-y_{1})^2}$, podemos encontrar $latex d_{1}, ~ d_{2}$ e $latex d_{3}$, que são as distâncias do circuncentro aos vértices A, B e C respectivamente:
$latex d_{1}=\sqrt{(x-x_{1})^2+(y-y_{1})^2}$
$latex d_{2}=\sqrt{(x-x_{2})^2+(y-y_{2})^2}$
$latex d_{3}=\sqrt{(x-x_{3})^2+(y-y_{3})^2}$
Passo 2: Obteremos três equações em função das coordenadas do circuncentro (x, y). Usamos duas dessas equações e qualquer método de resolução de sistemas de equações para obter uma solução (x, y). A solução do sistema são as coordenadas do circuncentro.
Método 2: usando a fórmula do ponto médio
Passo 1: Usando a fórmula do ponto médio, $latex M(x, y)=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2 }} {2}\right)$, calculamos os pontos médios dos três lados do triângulo AB, BC, AC.
Passo 2: Calculamos os declives dos lados do triângulo AB, BC e AC usando a fórmula do declive:
$latex m_{1}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}$
$latex m_{2}=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}$
$latex m_{3}=\frac{y_{3}-y_{1}}{x_{3}-x_{1}}$
onde $latex m_{1}$ é o declive de AB, $latex m_{2}$ é o declive de BC e $latex m_{3}$ é o declive de AC.
Passo 3: Usamos as coordenadas do ponto médio e o declive de cada lado do triângulo para obter uma equação para sua mediatriz (reta perpendicular).
$latex (y-y_{1})=-\frac{1}{m}(x-x_{1})$
Passo 4: Usamos as equações de duas mediatrizes do triângulo para formar um sistema de equações. A solução do sistema de equações são as coordenadas do circuncentro.
Método 3: Usando a lei estendida dos senos
Passo 1: Usando a lei estendida dos senos, podemos obter o comprimento do raio do círculo circunscrito. A lei estendida dos senos é escrita da seguinte forma:
$latex \frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}=2R$
onde, a, b, c são os comprimentos dos lados do triângulo e R é o raio do círculo circunscrito.
Passo 2: Podemos usar a fórmula da distância com as coordenadas dos vértices para obter duas equações em termos das coordenadas do circuncentro.
Passo 3: Resolvemos com qualquer método de sistemas de equações e obteremos as coordenadas do circuncentro.
Método 4: Usando a fórmula do circuncentro
Se soubermos as coordenadas de todos os três vértices e as medidas de todos os três ângulos, podemos usar a fórmula do circuncentro para encontrar rapidamente as coordenadas do circuncentro:
$$O(x, y)=\left(\frac{x_{1}\sin(2A)+x_{2}\sin(2B)+x_{3}\sin(2C)}{\sin(2A)+\sin(2B)+\sin(2C)}, ~ \frac{y_{1}\sin(2A)+y_{2}\sin(2B)+y_{3}\sin(2C)}{\sin(2A)+\sin(2B)+\sin(2C)}\right)$$
onde, $latex A(x_{1}, y_{1})$, $latex B(x_{2}, y_{2})$, $latex C(x_{3}, y_{3})$ são os vértices do triângulo e A, B, C são os ângulos correspondentes.
Exemplos resolvidos do circuncentro de um triângulo
Nos exemplos a seguir, aplicamos o que aprendemos sobre o circuncentro de um triângulo.
EXEMPLO 1
Use a fórmula do ponto médio para encontrar as coordenadas do circuncentro do triângulo a seguir.
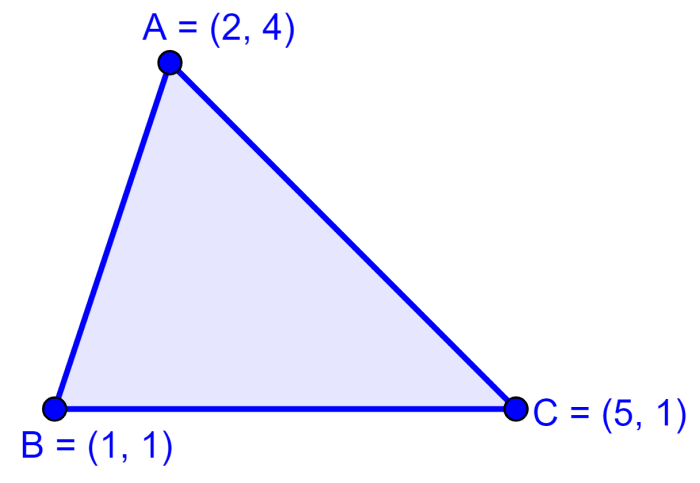
Solução
Usamos a fórmula do ponto médio para encontrar as coordenadas dos pontos médios dos lados do triângulo:
- $latex (x_{1},~y_{1})=(2, ~4)$
- $latex (x_{2},~y_{2})=(1,~1)$
- $latex (x_{3},~y_{3})=(5,~1)$
Ponto médio de AB:
$latex M_{1}=(\frac{2+1}{2}, \frac{4+1}{2})$
$latex M_{1}=(\frac{3}{2}, \frac{5}{2})$
Ponto médio CA:
$latex M_{3}=(\frac{2+5}{2}, \frac{4+1}{2})$
$latex M_{3}=(\frac{7}{2}, \frac{5}{2})$
Agora, temos que determinar os declives de AB e AC.
Declive de AB:
$latex m_{AB}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}$
$latex m_{AB}=\frac{4-1}{2-1}$
$latex m_{AB}=3$
Declive de AC:
$latex m_{BC}=\frac{y_{3}-y_{1}}{x_{3}-x_{1}}$
$latex m_{BC}=\frac{1-4}{5-2}$
$latex m_{BC}=-1$
Agora, temos que determinar as equações das retas perpendiculares aos lados e que passam pelos pontos médios encontrados.
$latex (y-y_{1})=-\frac{1}{m}(x-x_{1})$ (1)
$latex (y-\frac{5}{2})=-\frac{1}{3}(x-\frac{3}{2})$ (1)
$latex 6y-15=-2x+3$
$latex 6y+2x=18$
$latex 3y+x=9$
$latex (y-y_{1})=-\frac{1}{m}(x-x_{1})$ (2)
$latex (y-\frac{5}{2})=-\frac{1}{-1}(x-\frac{7}{2})$ (2)
$latex 2y-5=2x-7$
$latex 2y-2x=-2$
$latex y-x=-1$
Usando qualquer método para resolver o sistema de equações, obtemos x=3, y=2, que são as coordenadas do circuncentro.
EXEMPLO 2
O círculo passa pelos três vértices do triângulo a seguir, por isso é circunscrito. Qual é a sua área?
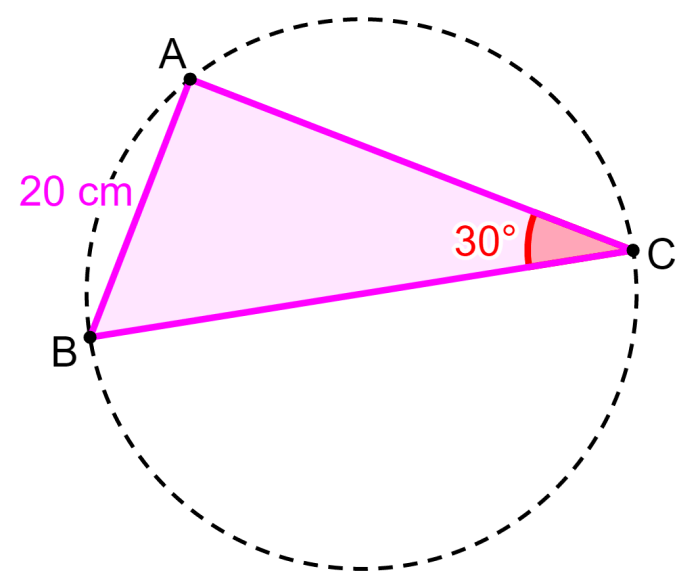
Solução
Podemos encontrar o raio do círculo circunscrito usando a lei estendida dos senos:
$latex \frac{a}{\sin (A)}=\frac{b}{\sin (B)}=\frac{c}{\sin (C)}=2R$
$latex \frac{20}{\sin (30)}=2R$
$latex R=20$ cm
Agora, podemos encontrar a área do círculo facilmente:
$latex A=\pi r^2$
$latex A=\pi (20)^2$
$latex A=400\pi$ cm²
EXEMPLO 3
Quais são as coordenadas do circuncentro do seguinte triângulo retângulo isósceles?
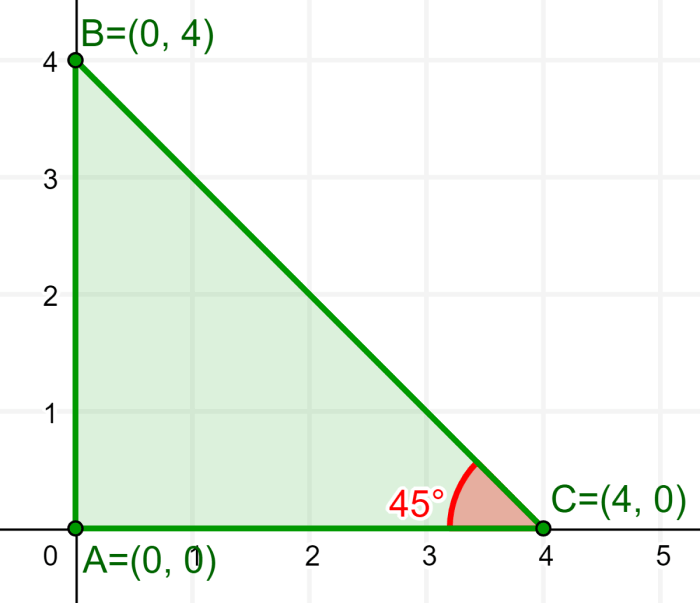
Solução
Podemos usar a fórmula do circuncentro, pois temos as coordenadas dos vértices e a medida dos ângulos.
O triângulo é um triângulo retângulo isósceles, o que significa que tem um ângulo de 90° em A e dois ângulos de 45° em B e C. Além disso, sabemos que seno de 90° é igual a 1 e seno de 180° é igual a 0. Então, temos :
$$O(x, y)=\left(\frac{x_{1}\sin(2A)+x_{2}\sin(2B)+x_{3}\sin(2C)}{\sin(2A)+\sin(2B)+\sin(2C)}, \frac{y_{1}\sin(2A)+y_{2}\sin(2B)+y_{3}\sin(2C)}{\sin(2A)+\sin(2B)+\sin(2C)}\right)$$
$latex O(x, y)=(\frac{(0+0+4 \times 1}{0+1+1},~\frac{0+4\times 1+0}{0+1+1})$
$latex O(x, y)=(\frac{4}{2},~\frac{4}{2})$
$latex O(x, y)=(2,~2)$
Exercícios para resolver do circuncentro de um triângulo
Resolva os exercícios a seguir usando o método apropriado para obter informações sobre o circuncentro de um triângulo.
Veja também
Interessado em aprender mais sobre o baricentro, incentro, ortocentro e circuncentro de um triângulo? Veja estas páginas:



