O incentro de um triângulo pode ser encontrado traçando as bissetrizes dos ângulos do triângulo e encontrando seu ponto de interseção. Além disso, também podemos calcular as coordenadas do incentro usando uma fórmula com as coordenadas dos vértices e os comprimentos dos lados do triângulo.
Neste artigo, aprenderemos como encontrar o incentro de um triângulo usando um método gráfico e um método algébrico. Em seguida, vamos resolver alguns exercícios práticos.
O que é o incentro de um triângulo?
O incentro de um triângulo é o ponto de intersecção das três bissetrizes do triângulo. Por sua vez, as bissetrizes são os segmentos que dividem os ângulos ao meio como podemos ver no diagrama:
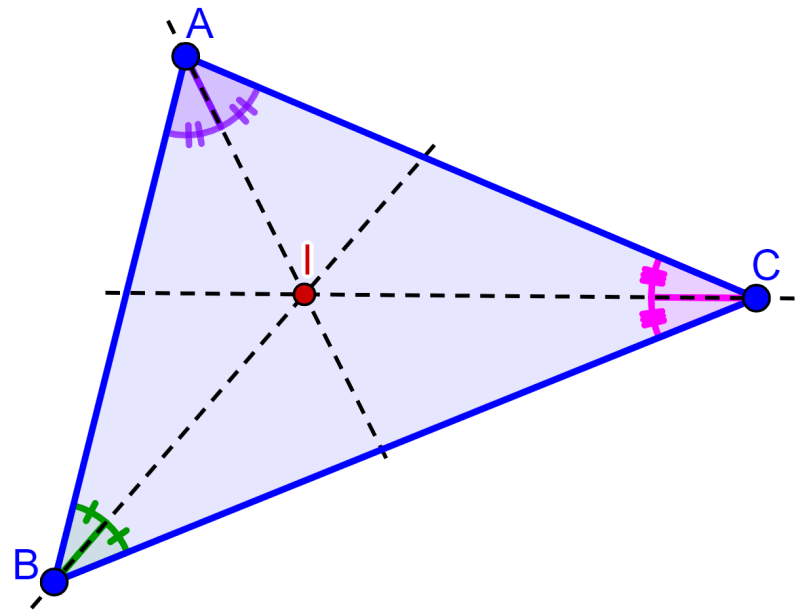
Alternativamente, podemos definir o incentro de um triângulo como o centro de um círculo inscrito no triângulo. Por sua vez, um círculo inscrito é o maior círculo que cabe dentro do triângulo.
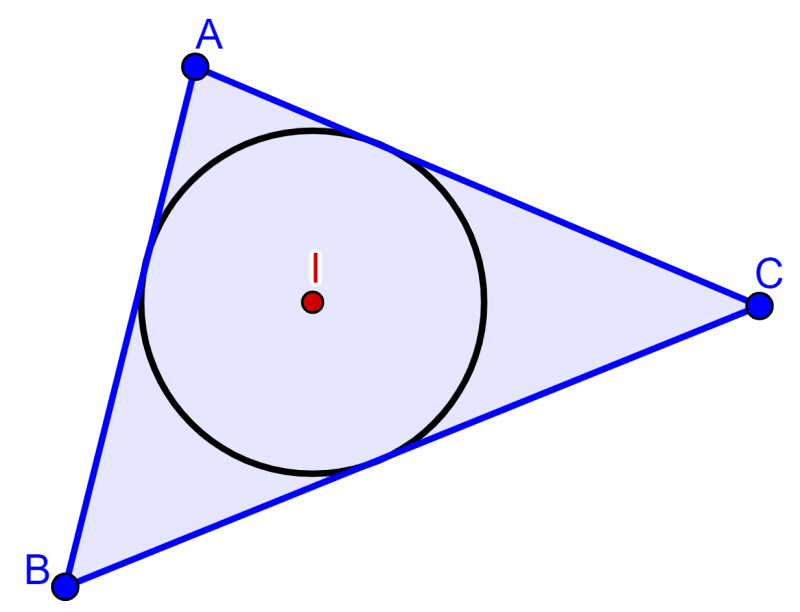
Propriedades do incentro de um triângulo
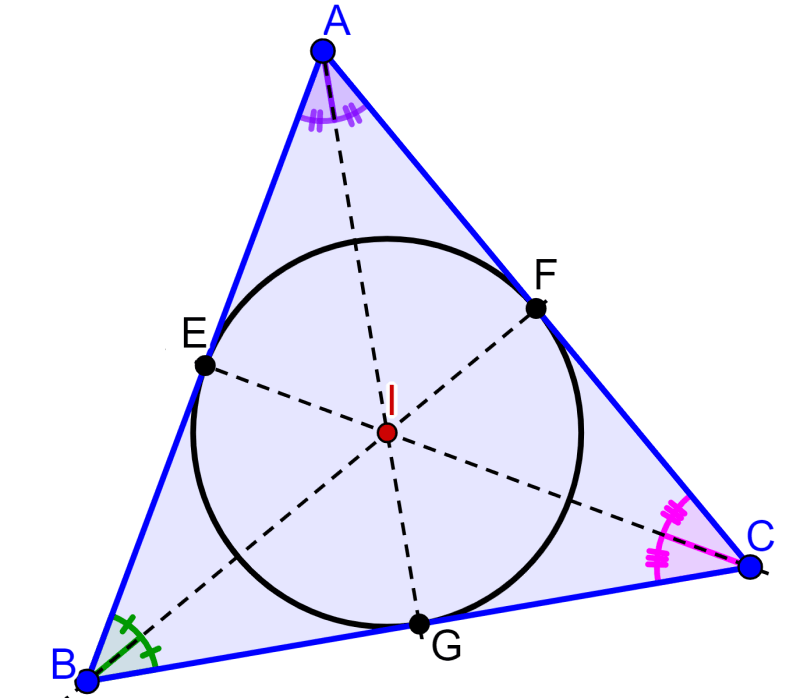
Propiedade 1: O incentro de um triângulo está sempre localizado dentro do triângulo, independentemente do tipo de triângulo que temos.
Propiedade 2: Se I é o incentro do triângulo, então os segmentos AE e AF devem ter o mesmo comprimento. O mesmo acontece com os segmentos BE e BG, e com os segmentos CG e CF.
Propiedade 3: Se I é o incentro do triângulo, então os ângulos ∠ABI e ∠CBI são iguais. O mesmo acontece com os ângulos ∠BAI e ∠CAI, e com os ângulos ∠ACI e ∠BCI.
Propiedade 4: Os lados do triângulo são tangentes ao círculo inscrito, então IE, IF e IG são iguais ao raio do círculo e são chamados de raio.
Propiedade 5: A área do triângulo pode ser calculada usando a fórmula A=sr, onde r é o raio do triângulo e s é o semiperímetro. Por sua vez, o semiperímetro é $latex s=\frac{a+b+c}{2}$.
Encontrar o incentro de um triângulo graficamente
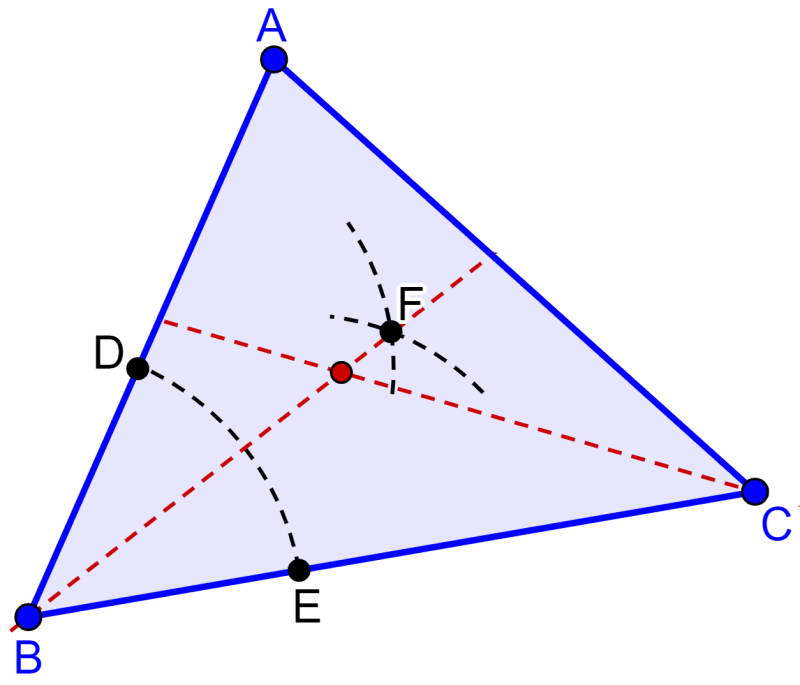
Podemos encontrar o incentro de um triângulo graficamente desenhando as bissetrizes dos ângulos e encontrando o ponto de interseção. Então, seguimos os seguintes passos usando um compasso:
Passo 1: Centramos o compasso no vértice B e, usando qualquer raio, desenhamos um arco que corta ambos os lados do triângulo. Assim, formamos os pontos D e E.
Passo 2: Com o mesmo raio, centralizamos o compasso nos pontos D e E para traçar dois arcos e formar o ponto de interseção F.
Passo 3: Desenhamos um segmento que passa pelos pontos B e F. Esse segmento é a bissetriz do ângulo B.
Passo 4: Repetindo o mesmo processo usando outro vértice do triângulo, podemos desenhar outra bissetriz.
Passo 5: Encontramos o ponto de intersecção de duas bissetrizes.
O ponto de interseção representa o incentro do triângulo.
Encontrar o incentro de um triângulo algebricamente
As coordenadas do incentro do triângulo podem ser obtidas algebricamente usando uma fórmula. No entanto, precisamos conhecer as coordenadas de todos os três vértices e os comprimentos de todos os três lados.
Suponha que temos o seguinte triângulo:
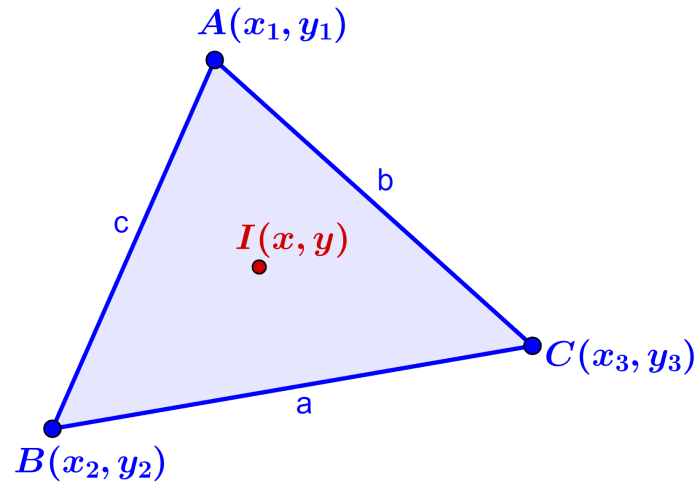
Assim, podemos calcular o incentro usando a seguinte fórmula:
$$\left(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c},~\frac{ay_{1}+by_{2}+cy_{3}}{a+b+c}\right)$$
onde, $latex A(x_{1},~y_{1})$, $latex B(x_{2},~y_{2})$ e $latex C(x_{3},~y_{3 } )$ são as coordenadas dos três vértices do triângulo e a, b, c são os lados opostos a cada vértice.
Exemplos resolvidos do incentro de um triângulo
Nos exemplos a seguir, podemos ver como encontrar as coordenadas do incentro de um triângulo algebricamente.
EXEMPLO 1
I representa o incentro do triângulo a seguir. Qual é a medida do ângulo x?
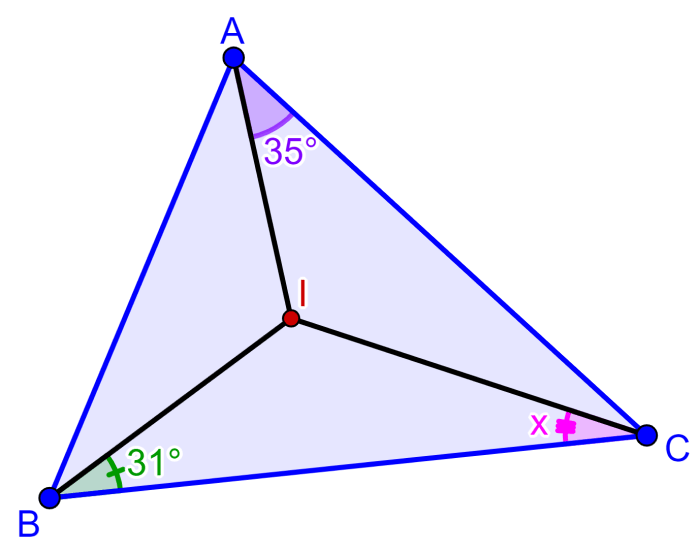
Solução: Como I é o incentro do triângulo, os segmentos que ligam o incentro aos vértices são bissetrizes, então eles dividem os ângulos em duas partes iguais.
Isso significa que os três ângulos internos do triângulo são:
2×35°=70°
2×31°=62°
2×x=2x
Um triângulo sempre tem a soma dos ângulos internos igual a 180°, então temos:
70°+62°+2x=180°
2x=180°-70°-62°
2x=48°
x=24°
EXEMPLO 2
Um triângulo tem uma área de 15 m² e seu perímetro é igual a 18 m. Qual é o raio do círculo inscrito no triângulo?
Solução: Temos o seguinte:
- Área do triângulo = 15 m²
- Perímetro do triângulo = 18 m
A área de um triângulo pode ser calculada usando A=sr, onde s é o semiperímetro e r é o raio. O semiperímetro é metade do perímetro. Então temos:
A=sr
15=9r
r=1,67
Portanto, o raio do círculo inscrito é 1,67 m.
EXEMPLO 3
O triângulo abaixo tem vértices A(0, 4), B(0, 1) e C(4, 4). Quais são as coordenadas de seu incentro?
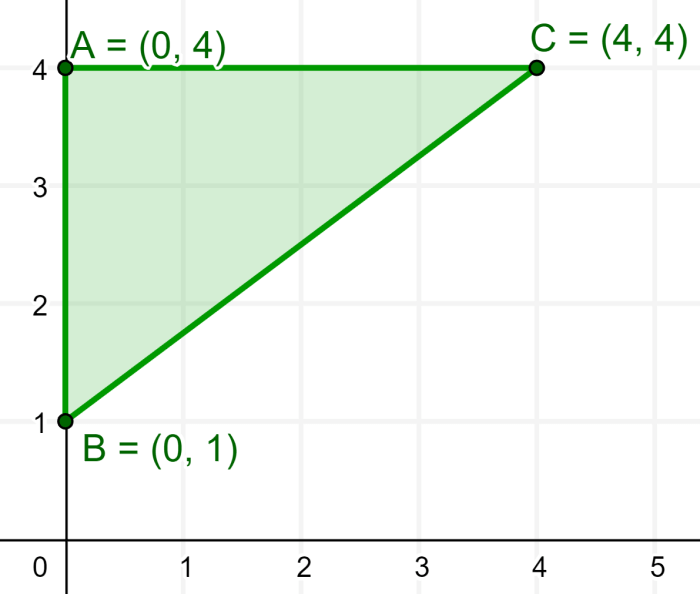
Solução: Podemos usar a fórmula do incentro junto com as coordenadas dos vértices e os comprimentos dos lados.
Usando o diagrama, podemos ver que o comprimento de b é 4 unidades e o comprimento de c é 3 unidades. Então, usamos o teorema de Pitágoras com esses dois lados para encontrar o comprimento de a:
a²=b²+c²
a²=4²+3²
a²=16+9
a²=25
a=5
Usando a fórmula do incentro, temos:
$$\left(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c},~\frac{ay_{1}+by_{2}+cy_{3}}{a+b+c}\right)$$
$$=\left(\frac{0+0+3(4)}{5+4+3},~\frac{5(4)+4(1)+3(4)}{5+4+3}\right)$$
$latex =(\frac{12}{12},~\frac{36}{12})$
$latex =(1,~3)$
As coordenadas do incentro são (1, 3).
Exercícios para resolver do incentro de um triângulo
Resolva os exercícios a seguir usando o método algébrico para encontrar as coordenadas do incentro.
Veja também
Interessado em aprender mais sobre o baricentro, incentro, ortocentro e circuncentro de um triângulo? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
