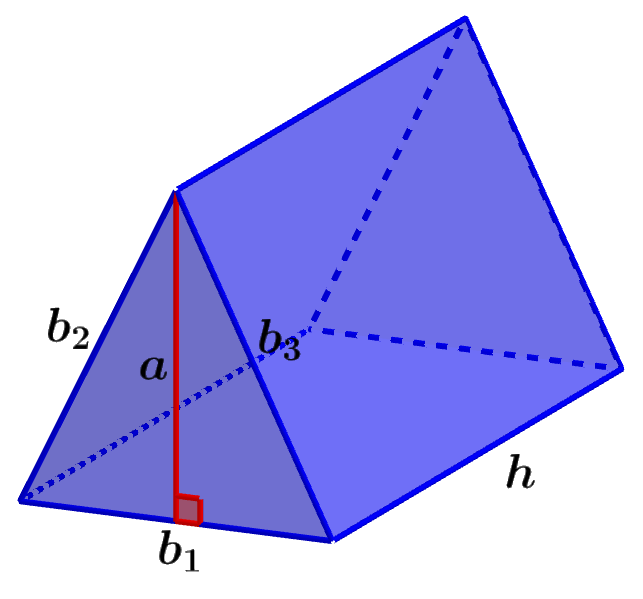
Um prisma triangular é uma figura geométrica tridimensional. Esses prismas são poliedros compostos por duas bases triangulares e três faces retangulares laterais. Semelhante a outros prismas, as duas bases são paralelas e congruentes uma com a outra. Os prismas triangulares têm 5 faces, 6 vértices e 9 arestas. As arestas e vértices são conectados uns aos outros por meio de três retângulos laterais. Esses prismas são pentaedros que possuem nove redes geométricas diferentes.
A seguir, aprenderemos mais sobre as características dos prismas triangulares e usaremos diagramas para ilustrar os conceitos.
Definição de um prisma triangular
Um prisma triangular é um tipo de prisma que possui duas bases e três faces laterais. As faces laterais são retangulares e as bases triangulares. No total, esses prismas têm cinco faces, nove vértices e seis arestas.
As faces laterais e bases do prisma triangular podem ou não ser congruentes dependendo se a base é um triângulo equilátero. As arestas do prisma unem-se às faces laterais correspondentes. As arestas dos triângulos são paralelas entre si.
Características fundamentais do prisma triangular
A seguir estão algumas das características mais importantes dos prismas triangulares:
- Eles têm um total de 9 arestas.
- Eles têm um total de 5 faces.
- Eles têm um total de 6 vértices.
- Eles têm duas faces triangulares, chamadas bases, e três faces retangulares, chamadas faces laterais.
- As bases são paralelas e congruentes entre si.
- Se as bases são triângulos equiláteros, as faces laterais são iguais entre si.
Fórmulas importantes do prisma triangular
Os prismas triangulares são figuras tridimensionais, portanto, suas propriedades mais importantes são o volume e a área de superfície.
Fórmula do volumen do prisma triangular
O volume de um prisma é encontrado multiplicando a área de sua base pelo comprimento de sua altura. As bases são triangulares e sabemos que a área de qualquer triângulo é igual a metade da base vezes a altura do triângulo. Portanto, temos a fórmula:
| $latex V=\frac{1}{2}bah$ |
onde, b representa o comprimento da base do triângulo, a representa a altura do triângulo e h representa a altura do prisma.
Fórmula da área do prisma triangular
Podemos encontrar a área do prisma triangular adicionando as áreas de todas as faces do prisma. Temos duas faces triangulares que são iguais, então a área de ambas as faces é ba. A área das faces laterais é igual ao comprimento do retângulo vezes sua altura.
Se tivermos um prisma com uma base de triângulo equilátero, a área da superfície é:
| $latex A_{s}=ba+3bh$ |
onde, a representa a altura do triângulo, b representa a base ou um dos lados do triângulo e h representa a altura do prisma.
Exercícios com prisma retangular
Os exercícios seguintes são resolvidos aplicando as fórmulas de prismas retangulares vistas acima.
EXERCÍCIO 1
Um prisma triangular tem um comprimento de base de 6 m e uma altura de 5 m. Se a altura do prisma for 7 m, qual é o volume do prisma?
Solução: Da questão, temos os valores $latex b = 6$, $latex a = 5$ e $latex h = 7$. Então, usamos esses valores na fórmula do volume:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(6)(5)(7)$
$latex V=105$
O volume do prisma é de 105 m³.
EXERCÍCIO 2
Se um prisma tem base triangular de base 8 m e altura de 6 m, qual é o seu volume com altura de 10 m?
Solução: Substituímos os valores fornecidos na fórmula do volume:
$latex V=\frac{1}{2}bah$
$latex V=\frac{1}{2}(8)(6)(10)$
$latex V=240$
O volume do prisma triangular é de 240 m³.
EXERCÍCIO 3
Um prisma tem uma base que é um triângulo equilátero com lados de 6 m de comprimento e 5,2 m de altura. Se a altura do prisma é de 10 m, qual é a sua área de superfície?
Solução: Temos os valores $latex b = 6$, $latex a = 5,2$ e $latex h = 10$, então usamos esses valores na fórmula para área de superfície:
$latex A_{s}=ba+3bh$
$latex A_{s}=(6)(5,2)+3(6)(10)$
$latex A_{s}=31,2+180$
$latex A_{s}=211,2$
A área de superfície é de 211,2 m².
EXERCÍCIO 4
Qual é a área da superfície de um prisma que tem uma altura de 9 m e uma base triangular com lados de 12 m de comprimento e 10,4 m de altura?
Solução: Temos os comprimentos $latex h = 9$, $latex b = 12$ e $latex a = 10,4$. Usando esses valores na fórmula de volume, temos:
$latex A_{s}=ba+3bh$
$latex A_{s}=(12)(10,4)+3(12)(9)$
$latex A_{s}=124,8+324$
$latex A_{s}=448,8$
A área de superfície é de 448,8 m².
Veja também
Você quer aprender mais sobre prisma triangular? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
