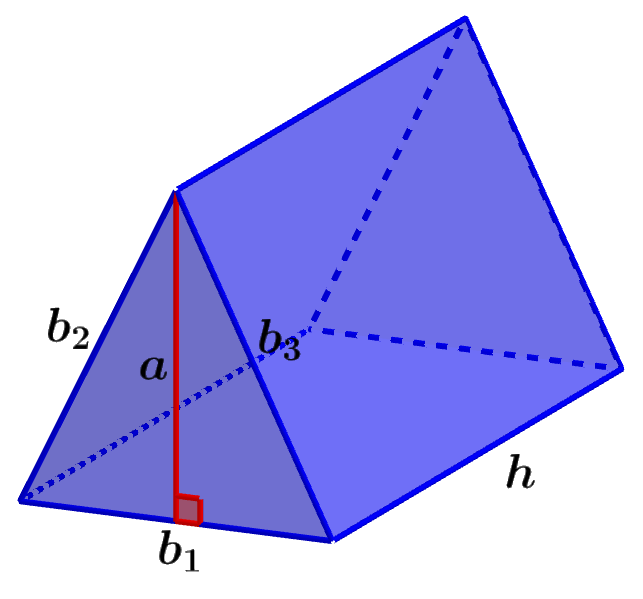
A área do prisma triangular é a área total coberta pelo prisma. A área de superfície é uma medida bidimensional, portanto podemos usar m², cm² ou outros. Para calcular a área da superfície de qualquer figura 3D, temos que adicionar as medidas das áreas de todas as faces da figura. Um prisma triangular tem duas faces triangulares iguais e três faces retangulares.
A seguir, saberemos a fórmula que podemos usar para calcular a área da superfície de um prisma retangular. Além disso, usaremos esta fórmula para resolver alguns exercícios práticos.
Fórmula para a área do prisma triangular
A fórmula para a área do prisma triangular é obtida adicionando as expressões para as áreas de todas as faces do prisma. Em um prisma triangular, temos duas faces triangulares iguais e três faces retangulares que podem ou não ser iguais.
Cada face triangular possui uma área de $latex \frac{1}{2} ab$, onde a é o comprimento da altura da base triangular e b é o comprimento de sua base. Isso significa que a área de ambas as faces triangulares é ab.
A área de cada face retangular é igual à altura do prisma multiplicada pelos três lados da base triangular. Ou seja, temos as áreas $latex b_{1}h, ~b_{2}h$ e $latex b_{3}h$, onde, $latex b_{1}, ~ b_{2}, ~ b_{3}$ são os comprimentos dos lados de a base triangular e h é o comprimento da altura do prisma.
Portanto, ao adicionar todas essas áreas, temos:
| $latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$ |
No caso da base ser um triângulo equilátero, sabemos que os três lados do triângulo são iguais, então as três áreas das faces laterais são iguais.
Exercícios de área do prisma triangular resolvidos
Os exercícios a seguir são usados para praticar o uso da fórmula para a área de superfície de prismas triangulares. Tente resolver os exercícios sozinho antes de olhar para a solução.
EXERCÍCIO 1
Um prisma triangular tem uma altura de 6 m e sua base triangular tem lados de 5 m, 6 m, 5 m de comprimento e 4 m de altura. Qual é a sua área de superfície?
Solução
Podemos obter as seguintes informações:
- Altura do prisma, $latex h=6$
- Lado 1, $latex b_{1}=5$
- Lado 2, $latex b_{2}=6$
- Lado 3, $latex b_{3}=5$
- Altura do triângulo, $latex a=4$
Usamos a fórmula para área de superfície e substituímos os valores dados:
$latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$
$$A_{s}=(4)(6)+(5)(6)+(6)(6)+(5)(6)$$
$latex A_{s}=24+30+36+30$
$latex A_{s}=120$
A área é de 120 m².
EXERCÍCIO 2
Um prisma triangular tem uma altura de 10 m e sua base triangular tem lados de 13 m, 10 m, 13 m e uma altura de 12 m. Qual é a sua área de superfície?
Solução
Temos os seguintes valores:
- Altura do prisma, $latex h=10$
- Lado 1, $latex b_{1}=13$
- Lado 2, $latex b_{2}=10$
- Lado 3, $latex b_{3}=13$
- Altura do triângulo, $latex a=12$
Usamos esses valores na fórmula para área de superfície e temos:
$latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$
$$A_{s}=(12)(10)+(13)(10)+(10)(10)+(13)(10)$$
$latex A_{s}=120+130+100+130$
$latex A_{s}=480$
A área é de 480 m².
EXERCÍCIO 3
Temos um prisma triangular de base equilátera com lados de 6 m e altura de 5,2 m. Se a altura do prisma é de 5 m, qual é a sua área de superfície?
Solução
Neste caso, temos um triângulo equilátero, então sabemos que os lados do triângulo são iguais. Então, temos:
- Altura do prisma, $latex h=5$
- Lado, $latex b=6$
- Altura do triângulo, $latex a=5,2$
Usamos a fórmula da área de superfície com esses dados e combinamos as três áreas dos lados laterais, uma vez que são iguais:
$latex A_{s}=ab+bh+bh+bh$
$latex A_{s}=ab+3bh$
$latex A_{s}=(5,2)(6)+3(6)(5)$
$latex A_{s}=31,2+90$
$latex A_{s}=121,2$
A área de superfície é de 121,2 m².
EXERCÍCIO 4
Um prisma tem uma base que é um triângulo equilátero com lados de 9 m de comprimento e 7,8 m de altura. Se a altura do prisma é de 8 m, qual é a sua área de superfície?
Solução
Temos as seguintes informações:
- Altura do prisma, $latex h=8$
- Lado, $latex b=9$
- Altura do triângulo, $latex a=7,8$
Usamos a fórmula para área do prisma triangular e substituímos os valores dados:
$latex A_{s}=ab+b_{1}h+b_{2}h+b_{3}h$
$latex A_{s}=ab+3bh$
$latex A_{s}=(7,8)(9)+3(9)(8)$
$latex A_{s}=70,2+216$
$latex A_{s}=286,2$
A área de superfície é de 286,2 m².
Exercícios de área do prisma triangular para resolver
Pratique o uso da área de superfície de prismas triangulares para resolver os exercícios a seguir. Selecione uma resposta e verifique-a para se certificar de que selecionou a correta. Se precisar de ajuda com isso, você pode consultar os exercícios resolvidos acima.
Veja também
Você quer aprender mais sobre prisma triangular? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
