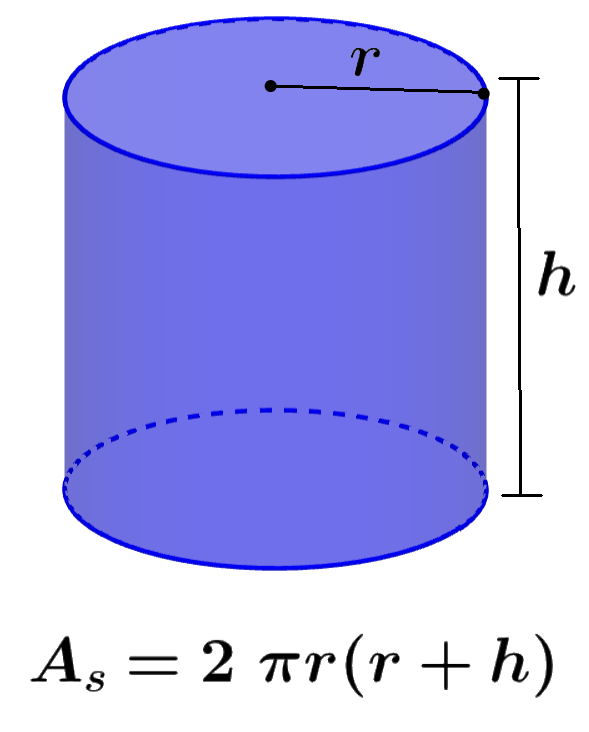
A área do cilindro é igual à área ocupada por a superfície do cilindro no espaço tridimensional. Um cilindro é uma figura geométrica tridimensional que possui duas bases circulares paralelas. Sabemos que um cilindro é composto de duas bases circulares e uma superfície que cobre as duas bases. Portanto, a área da superfície do cilindro é igual à área das duas bases circulares mais a área da superfície curva. A área do cilindro é representada em unidades quadradas, por exemplo, m².
A seguir, saberemos a fórmula que pode ser usada para calcular a área dos cilindros. Além disso, veremos alguns exercícios nos quais aplicaremos essa fórmula para encontrar a resposta.
Fórmula para a área do cilindro
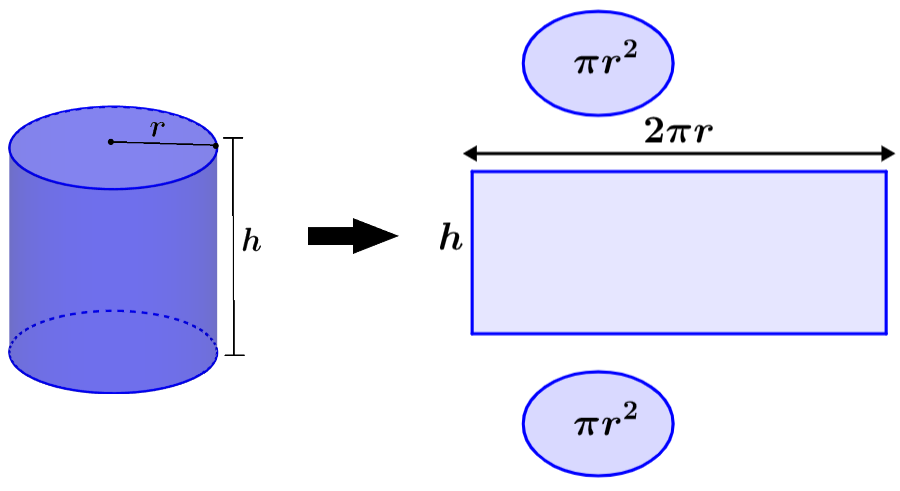
A área total de um cilindro é composta pelas seguintes partes:
- Área das bases
- Área de superfície curva
Área das bases
A base de um cilindro é uma figura circular. Portanto, podemos usar a fórmula para a área de um círculo. Como temos duas bases circulares, a área total das bases é:
$latex \text{Área bases}=2\pi{{r}^2}$
Área de superfície curvada
A área da superfície curva é dada pela área percorrida entre as bases de um cilindro de raio “r” e altura “h”. Esta área também é conhecida como área de superfície lateral. Podemos encontrar esta área com a seguinte fórmula:
$latex \text{Área lateral}=2\pi r h$
Área total do cilindro
A área total da superfície de um cilindro é igual à soma da área das duas bases mais a área da superfície curva. Então, temos:
| $latex A_{S}=2\pi {{r}^2}+2\pi r h$ ou $latex A_{S}=2\pi r(r+h)$ |
onde, $latex A_{S}$ representa a área da superfície do cilindro, r representa o comprimento do raio e h representa o comprimento da altura.
Exercícios de área do cilindro resolvidos
Os exercícios a seguir são resolvidos usando a fórmula para a área do cilindro. É recomendável que você tente resolver os exercícios sozinho antes de olhar para a resposta.
EXERCÍCIO 1
Qual é a área da superfície de um cilindro com raio de 5 m e altura de 8 m?
Solução
Temos os seguintes valores:
- Raio, $latex r=5$
- Altura, $latex h=8$
Usamos a fórmula para área o cilindro com estes valores:
$latex A_{S}=2\pi r(r+h)$
$latex A_{S}=2\pi (5)(5+8)$
$latex A_{S}=2\pi (5)(13)$
$latex A_{S}=408,4$
A área de superfície é de 408,4 m².
EXERCÍCIO 2
Um cilindro tem uma altura de 7 m e um raio de 6 m. Qual é a sua área de superfície?
Solução
A partir da pergunta, podemos obter o seguinte:
- Raio, $latex r=6$
- Altura, $latex h=7$
Colocamos esses valores na fórmula para a área do cilindro:
$latex A_{S}=2\pi r(r+h)$
$latex A_{S}=2\pi (6)(6+7)$
$latex A_{S}=2\pi (6)(13)$
$latex A_{S}=490,1$
A área é de 490,1 m².
EXERCÍCIO 3
Se um cilindro tem altura de 12 m e raio de 8 m, qual é sua área de superfície?
Solução
Temos os seguintes valores:
- Raio, $latex r=8$
- Altura, $latex h=12$
Usamos esses valores na fórmula para área de superfície:
$latex A_{S}=2\pi r(r+h)$
$latex A_{S}=2\pi (8)(8+12)$
$latex A_{S}=2\pi (8)(20)$
$latex A_{S}=1005,3$
A área de superfície é de 1005,3 m².
EXERCÍCIO 4
Se um cilindro tem um diâmetro de 6 m e uma altura de 7 m, qual é a sua área de superfície?
Solução
Neste caso, temos o diâmetro em vez do raio. No entanto, podemos obter o raio simplesmente dividindo o diâmetro por 2. Portanto, temos:
- Raio, $latex r=3$
- Altura, $latex h=7$
Usando a fórmula com esses valores, temos:
$latex A_{S}=2\pi r(r+h)$
$latex A_{S}=2\pi (3)(3+7)$
$latex A_{S}=2\pi (3)(10)$
$latex A_{S}=188,5$
A área de superfície é de 188,5 m².
EXERCÍCIO 5
Qual é a área da superfície de um cubo com 12 m de diâmetro e 13 m de altura?
Solução
Semelhante ao exercício anterior, dividimos o diâmetro por 2 para obter o raio. Então, temos:
- Raio, $latex r=6$
- Altura, $latex h=13$
Usando esses valores na fórmula para área de superfície, temos:
$latex A_{S}=2\pi r(r+h)$
$latex A_{S}=2\pi (6)(6+13)$
$latex A_{S}=2\pi (6)(19)$
$latex A_{S}=716,3$
A área é 716.3 m².
Exercícios de área do cilindro para resolver
Pratique o uso da fórmula para a área dos cilindros, resolvendo os exercícios a seguir. Você pode consultar os exercícios resolvidos acima, caso precise de ajuda com esses problemas.
Veja também
Você quer aprender mais sobre cilindros? Olha para estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
