Os ângulos externos de polígonos são formados quando estendemos os lados de um polígono. A soma total desses ângulos é sempre igual a 360°. Então, se o polígono for regular, podemos dividir 360° pelo número de lados para encontrar a medida de um ângulo externo do polígono. Se o polígono for irregular, precisamos usar outros métodos para encontrar as medidas de cada ângulo.
A seguir, aprenderemos mais sobre os ângulos externos dos polígonos.
Soma dos ângulos externos de um polígono
A soma dos ângulos externos de qualquer polígono é sempre igual a 360°. Esta propriedade se aplica independentemente de o polígono ser regular ou irregular. Por exemplo, no diagrama abaixo, podemos ver os ângulos externos de um pentágono.
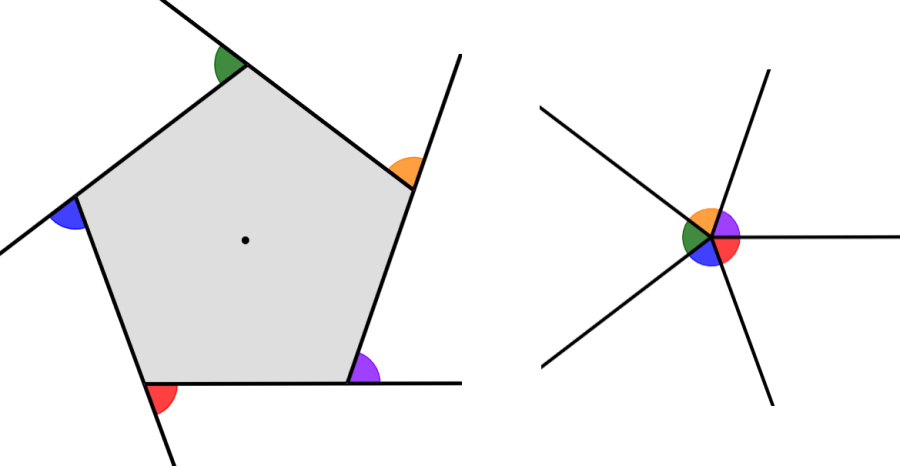
Podemos ver que quando os juntamos, os cinco ângulos externos formam um círculo. Isso representa uma volta completa, ou seja, um ângulo de 360°.
Agora, vamos ver o seguinte hexágono com seus ângulos externos.
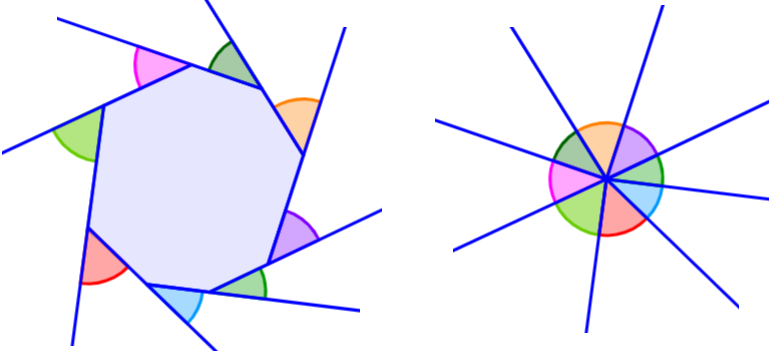
Da mesma forma, podemos observar que ao juntá-los, formamos um ângulo completo de 360°.
A soma é sempre igual a 360°. Isso significa que, à medida que os lados do polígono aumentam, as medidas dos ângulos externos individuais diminuem.
Ângulos externos de um polígono regular
Um polígono regular é uma figura geométrica com todos os seus lados com o mesmo comprimento e todos os seus ângulos internos com a mesma medida. Isso significa que todos os seus ângulos externos também têm a mesma medida.
Como a soma dos ângulos externos de qualquer polígono é sempre igual a 360°, podemos dividir pelo número de lados do polígono regular para obter a medida dos ângulos individuais.
Por exemplo, para um pentágono, temos que dividir 360° por 5:
360°÷5=72°
Cada ângulo externo de um pentágono regular mede 72°. Na tabela a seguir, podemos ver as medidas dos ângulos externos de alguns polígonos regulares comuns.
| Polígono | Cada ângulo |
| Triângulo | 120° |
| Quadrado | 90° |
| Pentágono | 72° |
| Hexágono | 60° |
| Heptágono | 51.43° |
| Octógono | 45° |
Como calcular as medidas dos ângulos externos de polígonos irregulares?
Podemos determinar a medida de um ângulo externo ausente se conhecermos as medidas dos outros ângulos externos. Para isso, temos que somar todos os ângulos conhecidos e subtrair de 360°.
Por exemplo, se temos os ângulos externos 60°, 70°, 80° e 85° em um pentágono, temos que começar determinando sua soma e depois subtrair de 360°:
60°+70°+80°+85°=295°
⇒ 360°-295°=65°
A medida do ângulo que falta é 65°.
Além disso, também podemos calcular as medidas dos ângulos externos se conhecermos as medidas dos ângulos internos. Para isso, consideramos que a soma de um ângulo interno e seu ângulo externo correspondente é igual a 180°.
Assim, podemos subtrair o ângulo interno de 180° para encontrar a medida do ângulo externo.
Por exemplo, se temos ângulos internos de 90°, 120°, 110°, 105° e 115° em um pentágono, temos que subtrair cada ângulo de 180° para encontrar os ângulos externos correspondentes:
180°-90°=90°
180°-120°=60°
180°-110°=70°
180°-105°=75°
180°-115°=65°
Assim, as medidas dos ângulos externos do pentágono são 90°, 60°, 70°, 75° e 65°.
Exemplos resolvidos de ângulos externos de polígonos
EXEMPLO 1
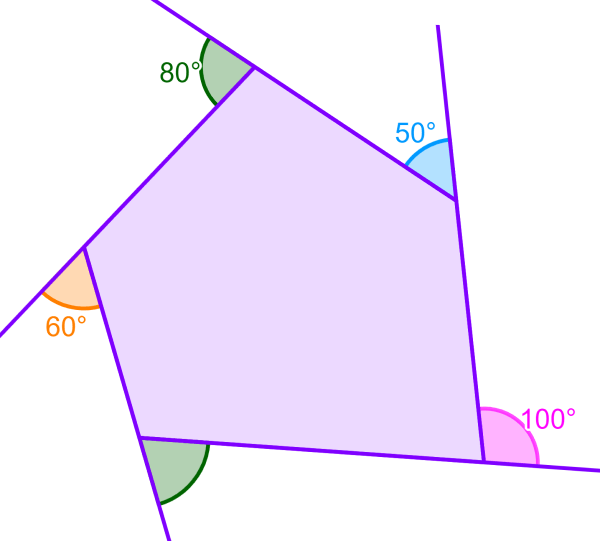
Determine as medidas dos ângulos externos ausentes no pentágono a seguir.
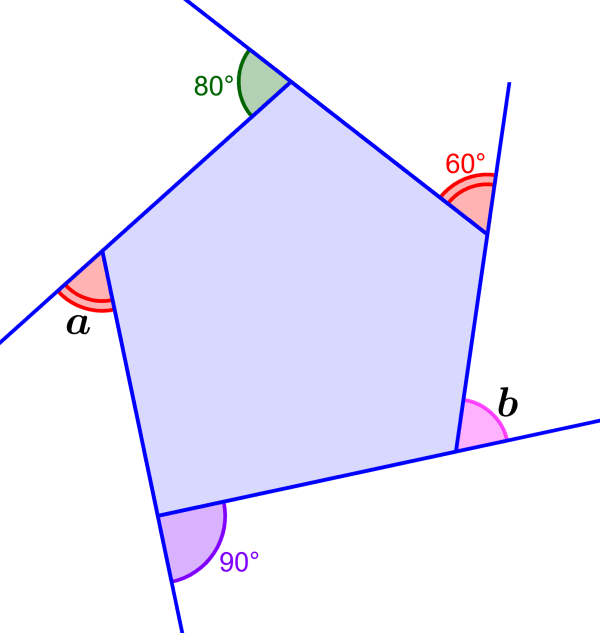
Solução: Os ângulos que têm a mesma cor e são representados por linhas duplas são iguais. Então, temos a = 60°. Para encontrar a medida do ângulo b, precisamos somar as medidas dos ângulos conhecidos e subtrair de 360°. Então temos:
80°+60°+60°+90°=290°
⇒ 360°-290°=70°
O ângulo b mede 70°.
EXEMPLO 2
Encontre as medidas dos ângulos externos ausentes no hexágono abaixo.
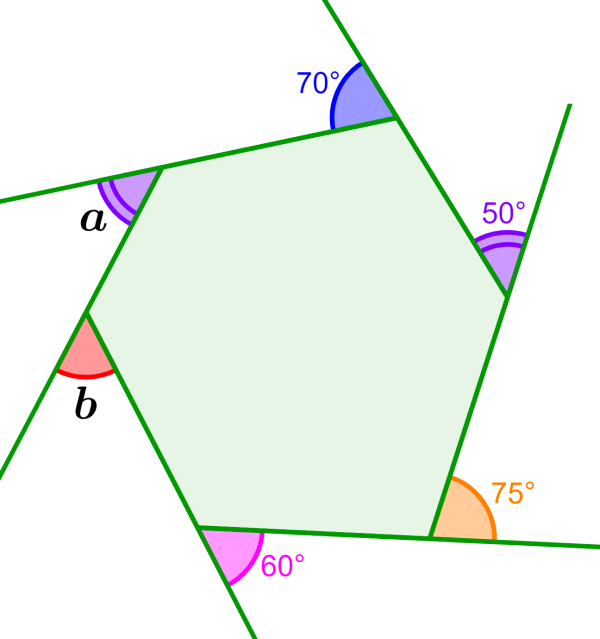
Solução: Ângulos marcados com linhas duplas e com a mesma cor compartilham a mesma medida, então temos a=50°. Para encontrar a medida do ângulo b, precisamos somar as medidas dos ângulos conhecidos e subtrair o resultado de 360°. Então temos:
50°+50°+70°+75°+60°=305°
⇒ 360°-305°=55°
A medida do ângulo b é 55°.
EXEMPLO 3
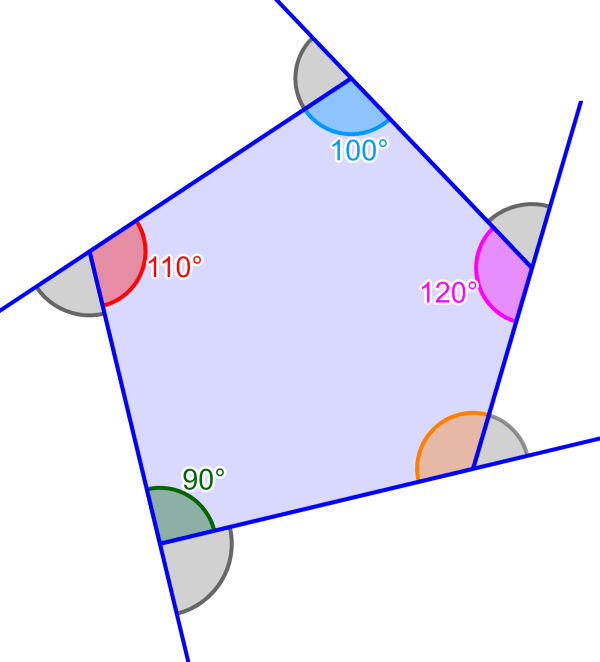
Encontre as medidas dos ângulos externos do pentágono.
Solução: Precisamos subtrair cada ângulo interno correspondente de 180° para encontrar as medidas dos ângulos externos. Então temos:
180°-110°=70°
180°-120°=60°
180°-100°=80°
180°-90°=90°
Agora, temos um ângulo ausente. Podemos encontrar esse ângulo adicionando os ângulos conhecidos e subtraindo de 360°:
70°+60°+80°+90°=300°
360°-300°=60°
EXEMPLO 4
Determine as medidas dos ângulos externos no hexágono a seguir.
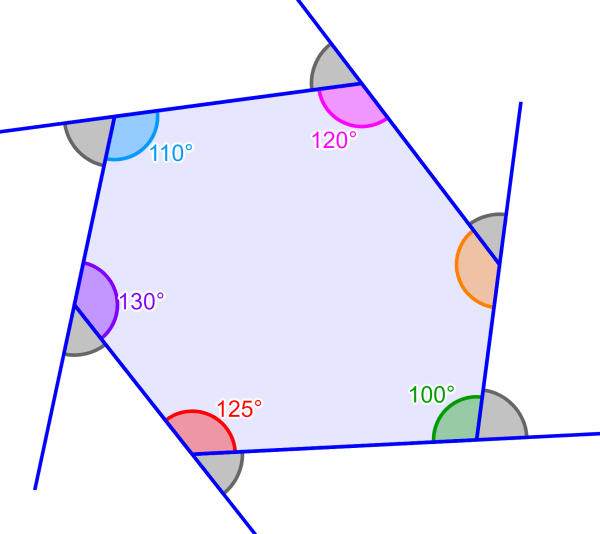
Solução: Neste caso, temos as medidas dos ângulos internos. Então, subtraímos cada ângulo de 180° para encontrar a medida do ângulo externo correspondente:
180°-110°=70°
180°-120°=60°
180°-130°=50°
180°-125°=55°
180°-100°=80°
Para encontrar a medida do ângulo externo ausente, podemos somar as medidas dos ângulos externos conhecidos e subtrair de 360°. Então nós temos:
70°+60°+50°+55°+80°=315°
⇒ 360°-315°=45°
Veja também
Interessado em aprender mais sobre ângulos externos? Veja estas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
