O ângulo entre duas retas nos permite determinar a inclinação que existe entre as retas. Podemos calcular o ângulo entre duas retas usando uma fórmula geral que usa os declives de ambas as retas. Esta fórmula pode ser derivada usando trigonometria.
A seguir, aprenderemos como usar os declives de duas retas para encontrar o ângulo entre elas. Usaremos a fórmula geral para resolver alguns exercícios práticos.
GEOMETRIA
Relevante para…
Aprenda a encontrar o ângulo entre duas retas com exercícios.
GEOMETRIA
Relevante para…
Aprenda a encontrar o ângulo entre duas retas com exercícios.
Formula do angulo entre duas retas
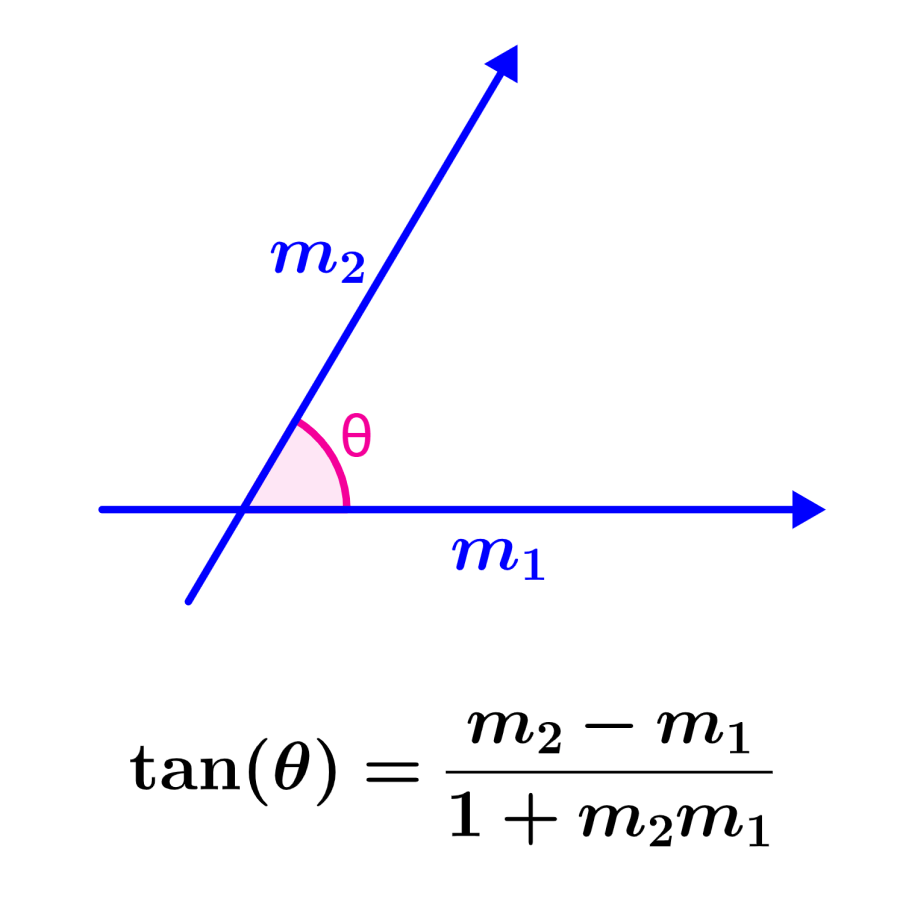
Se tivermos as duas retas $latex y=m_{1}x+c_{1}$ e $latex y=m_{2}x+c_{2}$, o ângulo entre as retas é dado pela seguinte fórmula:
| $$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$ |
onde, θ é o ângulo entre as retas , $latex m_{1}$ é o declive da primeira reta e $latex m_{2}$ é o declive da segunda reta conforme mostrado no diagrama a seguir:
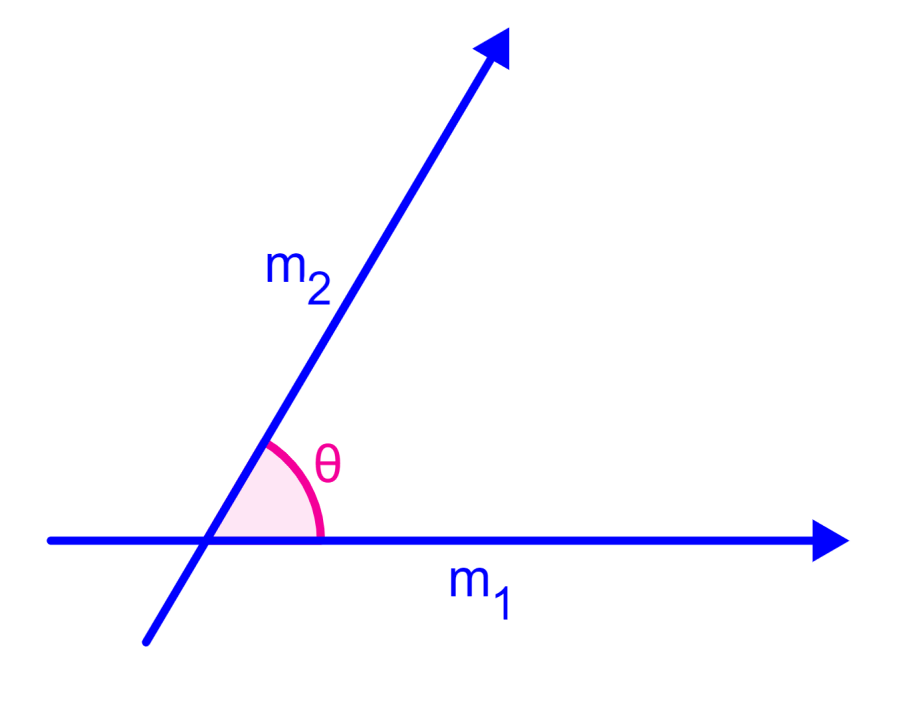
Você pode escolher os declives em qualquer ordem. Portanto, $latex m_{2}$ pode ser maior ou menor que $latex m_{1}$.
Prova da fórmula do ângulo entre duas retas
Para provar a fórmula do ângulo entre duas retas, vamos usar a trigonometria com o seguinte diagrama:
Aqui, temos as retas $latex y=m_{1}x+c_{1}$ e $latex y=m_{2}x+c_{2}$, que formam os ângulos α e β com o eixo x respectivamente.
Usando teoremas do ângulo, podemos determinar que $latex \theta = \beta – \alpha$. Então, temos o seguinte:
$latex \tan(\theta)=\tan(\beta -\alpha)$
Usando a fórmula de Identidades de Adição e Subtração de Ângulos para a tangente, temos:
$$\tan(\theta)=\frac{\tan(\beta)-\tan(\alpha)}{1+\tan(\beta)\tan(\alpha)}$$
Agora, podemos escrever $latex \tan(\beta)=m_{2}$ e $latex \tan(\alpha)=m_{1}$, pois essas são os declives das retas. Então temos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
Ângulo entre duas retas – Exercícios resolvidos
Os exercícios a seguir são resolvidos usando a fórmula do ângulo entre duas retas. Cada exercício tem sua respectiva solução, mas tente resolver os exercícios antes de olhar a resposta.
EXERCÍCIO 1
Encontre o ângulo entre as retas $latex y=x$ e $latex y=3x-4$.
Solução
Lembre-se que na forma $latex y=mx+b$, m é o declive da reta. Então temos:
- A reta $latex y=x$ tem um declive de 1, então $latex m_{1}=1$
- A reta $latex y=3x-4$ tem um declive de 3, então $latex m_{2}=3$
Usando a fórmula do ângulo entre duas retas, temos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{3-1}{1+(3)(1)}$$
$$\tan(\theta)=\frac{2}{4}$$
$$\tan(\theta)=\frac{1}{2}$$
$$\theta=\tan^{-1}\left(\frac{1}{2}\right)$$
$$\theta=26,6^{\circ}$$
EXERCÍCIO 2
Qual é o ângulo entre as retas $latex y=2x-5$ e $latex y=5x+6$?
Solução
Temos o seguinte:
- A reta $latex y=2x-5$ tem um declive de 2, então $latex m_{1}=2$
- A reta $latex y=5x+6$ tem um declive de 5, então $latex m_{2}=5$
Aplicando a fórmula do ângulo entre duas retas, temos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{5-2}{1+(5)(2)}$$
$$\tan(\theta)=\frac{3}{11}$$
$$\theta=\tan^{-1}\left(\frac{3}{11}\right)$$
$$\theta=15,26^{\circ}$$
EXERCÍCIO 3
Encontre o ângulo entre as retas $latex y=3+x$ e $latex y=6+2x$.
Solução
Podemos obter as seguintes informações:
- A reta $latex y=3+x$ tem um declive de 1, então $latex m_{1}=1$
- A reta $latex y=6+2x$ tem um declive de 2, então $latex m_{2}=2$
Usando a fórmula do ângulo entre duas retas, temos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{2-1}{1+(2)(1)}$$
$$\tan(\theta)=\frac{1}{3}$$
$$\theta=\tan^{-1}\left(\frac{1}{3}\right)$$
$$\theta=18,43^{\circ}$$
EXERCÍCIO 4
Determine o ângulo entre as retas $latex y=6x-7$ e $latex y=2-x$.
Solução
Temos o seguinte:
- A reta $latex y=6x-7$ tem um declive de 6, então $latex m_{1}=6$
- A reta $latex y=2-x$ tem um declive de -1, então $latex m_{2}=-1$
Usando a fórmula com esses valores, temos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-1-6}{1+(-1)(6)}$$
$$\tan(\theta)=\frac{-7}{-5}$$
$$\tan(\theta)=\frac{7}{5}$$
$$\theta=\tan^{-1}\left(\frac{7}{5}\right)$$
$$\theta=54,46^{\circ}$$
EXERCÍCIO 5
Qual é o ângulo entre as retas $latex y=2x+3$ e $latex y=5-2x$.
Solução
Podemos obter as seguintes informações:
- A reta $latex y=2x+3$ tem um declive de 2, então $latex m_{1}=2$
- A reta $latex y=5-2x$ tem um declive de -2, então $latex m_{2}=-2$
Aplicando a fórmula com esses valores, temos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-2-2}{1+(-2)(2)}$$
$$\tan(\theta)=\frac{-4}{-3}$$
$$\theta=\tan^{-1}\left(\frac{4}{3}\right)$$
$$\theta=53,13^{\circ}$$
EXERCÍCIO 6
Encontre o ângulo entre as retas $latex y=4-2x$ e $latex y=9-3x$
Solução
Temos o seguinte:
- A reta $latex y=4-2x$ tem um declive de -2, então $latex m_{1}=-2$
- A reta $latex y=9-3x$ tem um declive de -3, então $latex m_{2}=-3$
Usando a fórmula do ângulo entre duas retas, temos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-3-(-2)}{1+(-3)(-2)}$$
$$\tan(\theta)=\frac{-1}{7}$$
$$\theta=\tan^{-1}\left(-\frac{1}{7}\right)$$
$$\theta=8,13^{\circ}$$
EXERCÍCIO 7
Encontre o ângulo entre as retas $latex y=4$ e $latex 3y+2x-6=0$.
Solução
Temos o seguinte:
- A reta $latex y=4$ é horizontal e tem um declive de 0, então $latex m_{1}=0$
- A reta $latex 3y+2x-6=0$ pode ser escrita como $latex y=-2/3x+2$, então tem um declive de -2/3, $latex m_{2}=-2/ $3
Usando a fórmula do ângulo entre duas retas, temos:
$$\tan(\theta)=\frac{m_{2}-m_{1}}{1+m_{2}m_{1}}$$
$$\tan(\theta)=\frac{-2/3}{1+(-2/3)(0)}$$
$$\tan(\theta)=\frac{-2/3}{1}$$
$$\tan(\theta)=-\frac{2}{3}$$
$$\theta=\tan^{-1}\left(-\frac{2}{3}\right)$$
$$\theta=33,69^{\circ}$$
Ângulo entre duas retas – Exercícios para resolver
Aplique a fórmula do ângulo entre duas retas para resolver os exercícios a seguir. Se você tiver problemas com isso, você pode usar os exercícios resolvidos acima como um guia.
Veja também
Interessado em aprender mais sobre equações de retas? Dê uma olhada nessas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
