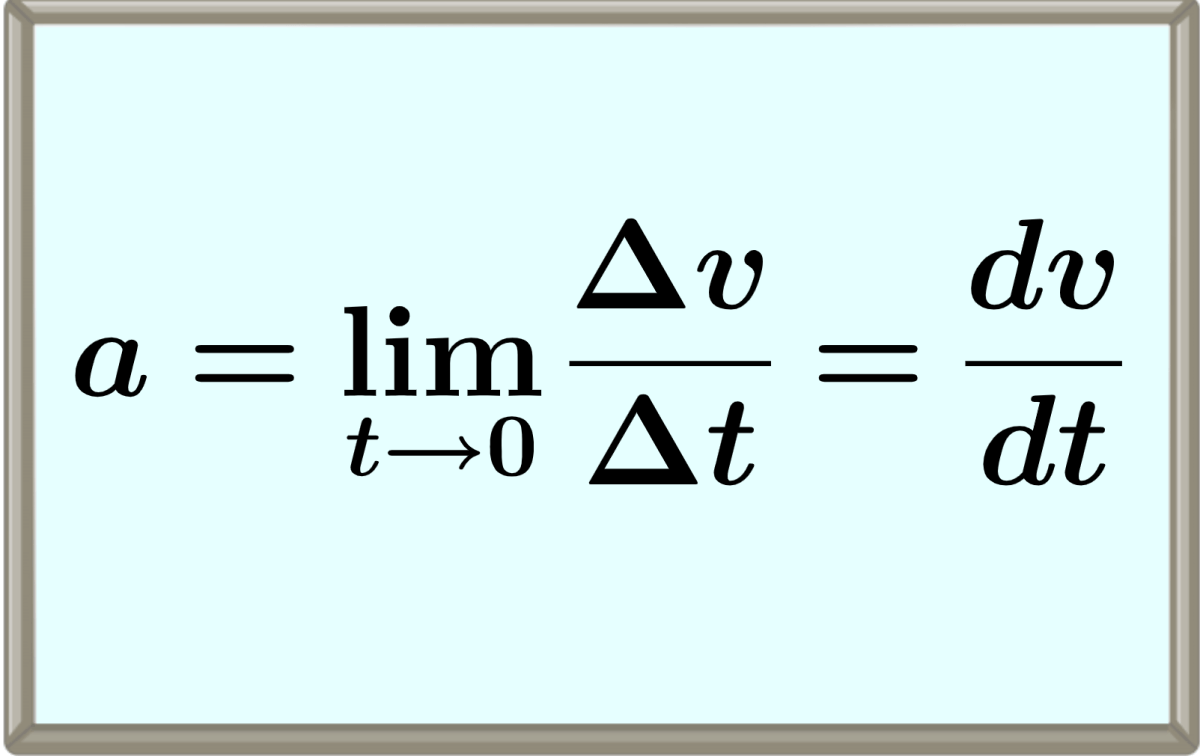A aceleração instantânea é uma medida de como a velocidade de um objeto muda em um instante específico no tempo. É o limite da aceleração média em um intervalo infinitesimalmente pequeno à medida que esse intervalo se aproxima de zero.
Embora muitas vezes discutamos a aceleração como uma taxa média, entender como ela pode mudar em um determinado instante nos dá uma visão mais precisa e diferenciada do movimento de um objeto. Neste artigo, veremos a aceleração instantânea em detalhes.
O que é velocidade instantânea em física?
A aceleração instantânea descreve a taxa de alteração na velocidade de um objeto em um determinado instante. É a aceleração que um objeto experimenta em um ponto específico no tempo.
Diferentemente da aceleração média, que fornece a taxa média de alteração da velocidade em um determinado intervalo de tempo, a aceleração instantânea se concentra em um ponto específico no tempo para medir a rapidez com que a velocidade está mudando naquele exato momento.
É importante lembrar que a aceleração, incluindo a aceleração instantânea, é uma quantidade vetorial. Isso significa que não tem apenas magnitude, mas também direção. A magnitude da aceleração instantânea nos informa a rapidez com que a velocidade muda em um determinado momento, enquanto a direção indica em que sentido a velocidade está mudando.
Matematicamente, a aceleração instantânea pode ser encontrada diferenciando a função de velocidade em relação ao tempo. No caso de uma função de posição $latex s(t)$, primeiro encontramos a função de velocidade $latex v(t)$ diferenciando $latex s(t)$ em relação ao tempo e, em seguida, encontramos a função de aceleração $latex a(t)$ diferenciando $latex v(t)$ em relação ao tempo.
Isso significa que a aceleração instantânea está profundamente ligada aos conceitos de taxa e mudança – ideias centrais do cálculo. A aceleração instantânea tem a ver com a compreensão da taxa instantânea de variação da velocidade.
Fórmula e cálculo da aceleração instantânea
A aceleração instantânea é o limite da aceleração média à medida que o intervalo de tempo se aproxima de zero. A fórmula da aceleração instantânea é expressa como:
$$a(t)= \lim\limits_{\Delta t\to 0} \frac{ \Delta v}{ \Delta t}$$
$$a = \frac{dv}{dt}$$
onde:
- $latex a$ é a aceleração instantânea,
- $latex dv$ é a mudança na velocidade, e
- $latex dt$ é a mudança no tempo.
Essa é essencialmente a derivada da velocidade com relação ao tempo. O “$latex d$” na fórmula denota um elemento diferencial ou uma mudança infinitesimalmente pequena. Assim, $latex \frac{dv}{dt}$ refere-se à alteração na velocidade ($latex dv$) por unidade de tempo ($latex dt$).
Cálculo da aceleração instantânea passo a passo
Vejamos o processo de encontrar a aceleração instantânea.
Passo 1: Identifique a função de velocidade. Geralmente, essa é uma função em termos de tempo.
Passo 2: Diferencie a função de velocidade. A função de aceleração é igual à derivada da função de velocidade com relação ao tempo.
Passo 3: Substitua o tempo necessário. Por exemplo, se quisermos encontrar a aceleração instantânea em $latex t = 3$ segundos. Substituímos $latex t = 3$ em nossa função de aceleração.
O método descrito acima nos permite determinar a aceleração instantânea em qualquer ponto no tempo, desde que tenhamos a função de velocidade do objeto. Se, em vez disso, tivermos a função de posição, precisaremos diferenciar duas vezes para encontrar a função de aceleração.
Aceleração instantânea – Exemplos com respostas
Vamos explorar alguns problemas relacionados a encontrar a aceleração instantânea. Esses exemplos pressupõem que você entenda os conceitos básicos de cálculo.
EXEMPLO 1
Dada a função de velocidade de uma partícula $latex v(t) = t^3 – 4t$ (em m/s), encontre a aceleração instantânea em $latex t = 2$ segundos.
Solução
Começamos encontrando a função de aceleração, $latex a(t)$. Para isso, tomamos a derivada da função de velocidade:
$latex a(t) = \dfrac{dv}{dt} = 3t^2 – 4$
Em seguida, substitua $latex t = 2$ na função de aceleração para encontrar a aceleração instantânea nesse momento:
$latex a(2) = 3(2)^2 – 4 = 8~ \text{m/s}^2$.
Portanto, a aceleração instantânea em $latex t = 2$ s é de 8 m/s².
EXEMPLO 2
Um objeto tem a função de posição $latex s(t) = 3t^3 – 2t^2 + 4$ (em metros). Qual é sua aceleração instantânea em $latex t=2$ segundos?
Solução
Primeiro, temos que encontrar a função de velocidade, $latex v(t)$, tomando a derivada da função de posição:
$latex v(t) = \dfrac{ds}{dt} = 9t^2 – 4t$
Em seguida, encontramos a função de aceleração, $latex a(t)$, tomando a derivada da função de velocidade:
$latex a(t) = \dfrac{dv}{dt} = 18t – 4$
Por fim, substitua $latex t = 2$ na função de aceleração para encontrar a aceleração instantânea nesse momento:
$latex a(2) = 18(2) – 4 = 32 ~\text{m/s}^2$
Portanto, a aceleração instantânea em $latex t = 2$ s é de 32 m/s².
EXEMPLO 3
Se um objeto tiver a função de velocidade $latex v(t) = \sin(t) + t^2$ (em m/s), encontre a aceleração instantânea em $latex t = \pi$ segundos.
Solução
Ao diferenciar a função de velocidade, encontramos a função de aceleração, $latex a(t)$:
$latex a(t) = \dfrac{dv}{dt} = \cos(t) + 2t$
Em seguida, substitua $latex t = \pi$ na função de aceleração para encontrar a aceleração instantânea nesse momento:
$latex a(\pi) = \cos(\pi) + 2\pi = -1 + 2\pi ~\text{m/s}^2$
Portanto, a aceleração instantânea em $latex t = \pi$ s é $latex -1 + 2\pi$ m/s².
EXEMPLO 4
Encontre a aceleração instantânea em $latex t=3$ segundos de um objeto com a função de posição $latex s(t) = t^4 – 6t^2$ (em metros).
Solução
Primeiro, diferencie a função de posição para encontrar a função de velocidade, $latex v(t)$:
$latex v(t) = \dfrac{ds}{dt} = 4t^3 – 12t$
Em seguida, diferencie a função de velocidade para encontrar a função de aceleração, $latex a(t)$:
$latex a(t) = \dfrac{dv}{dt} = 12t^2 – 12$
Por fim, substitua $latex t = 3$ na função de aceleração para encontrar a aceleração instantânea nesse momento:
$latex a(3) = 12(3^2) – 12 = 96 ~\text{m/s}^2$
Portanto, a aceleração instantânea em $latex t = 3$ s é de 96 m/s².
Aplicações da aceleração instantânea
A aceleração instantânea tem uma ampla gama de aplicações, especialmente em campos como a física e a engenharia. Aqui estão alguns exemplos:
Análise de movimento de veículos: A aceleração instantânea de um carro ou de qualquer veículo pode ser usada para estudar e analisar seu movimento. Por exemplo, compreender a rapidez com que um veículo pode acelerar é fundamental para projetar sistemas de freios e prever distâncias de parada.
Astronomia e Engenharia Espacial: Ao lançar naves espaciais ou estudar corpos celestes, o conceito de aceleração instantânea é fundamental. Ele é usado para calcular trajetórias de lançamento, manobrar naves espaciais e entender os movimentos de estrelas e planetas.
Esportes e biomecânica: Entender a aceleração instantânea também é essencial na ciência do esporte. Isso ajuda a melhorar o desempenho atlético, projetar programas de treinamento mais eficazes, prevenir lesões e até mesmo criar equipamentos mais ergonômicos.
Robótica e Automação: Na robótica, o conceito de aceleração instantânea é usado para controlar o movimento de robôs com precisão. Ele é importante em aplicações que vão desde a automação industrial até veículos autônomos.
Veja também
Interessado em saber mais sobre velocidade e aceleração? Dê uma olhada nestas páginas:
Jefferson Huera Guzman
Jefferson é o principal autor e administrador do Neurochispas.com. O conteúdo interativo de Matemática e Física que criei ajudou muitos alunos.
